SAS进行主成分分析（Principal Component Analysis，PCA）

进行主成分分析主要步骤如下：

　　1. 指标数据标准化（ SPSS软件自动执行），目的是消除不同量纲的影响；

　　2. 指标之间的相关性判定；

　　3. 确定主成分个数m；

　　4. 主成分Fi表达式；

　　5. 主成分Fi命名；

影响中国蔬菜产量的若干因素，收集了1990-2002年13年数据，

中国蔬菜生产、消费与贸易研究

汪晓银  

使用princomp过程进行主成分分析

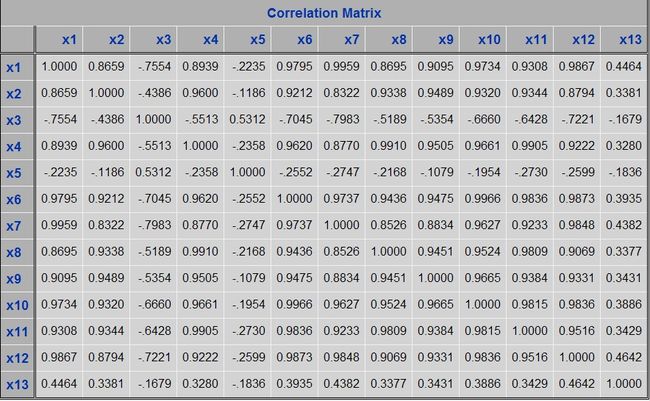
data ex;                                                                                                                                
input x1-x13@@;                                                                                                                         
 /*x1 种植面积 x2物质费用投入 x3劳动力投入 x4蔬菜价格 x5生产纯收益率 x6市场化程度 x7x8城市化水平1，2*/                                  
/*交通x9 x10城镇居民收入x11农村居民收入 x12农业劳动工受教育程度 x13气候条件 */                                                          
cards;                                                                                                                                  
6610    4620    792     100.00  121.2   725.95  26.41   22.6    8.49    1510    686     6.21    12.01                                   
6916    4749    891     106.10  123.77  812.96  26.94   22.79   8.51    1701    709     6.58    18.59                                   
7030    4189    821     116.29  89      938.29  27.46   23.43   8.93    2027    784     6.65    17.38                                   
8084    5131    861     134.54  127.34  1051.5  27.99   24.58   9.41    2577    922     6.78    15.66                                   
8921    6510    923     185.94  140.58  1357.1  28.51   25.72   9.85    3496    1221    6.88    21.17                                   
9514    8582    1032    240.42  146     1702.4  29.04   26.86   10.2    4283    1578    7.02    14.86                                   
10368   9036    795     284.65  104.10  2024.2  30.48   27.89   10.6    4839    1926    7.28    13.93                                   
11278   9069    818     283.23   99.70  2208.2  31.91   28.29   10.3    5160    2090    7.41    19.68                                   
12291   7464    694     284.08  102.59  2336.7  33.35   28.42   10.2    5425    2162    7.55    16.17                                   
13346   7905    699     285.22  115.56  2475.2  34.78   28.32   10.3    5854    2210    7.71    17.09                                   
15237   9669    705     303.19  92.72   2694.7  36.22   28.44   10.7    6280    2253    7.93    21.94                                   
16339   9794    680     312.89  113.72  2945.7  37.66   28.61   11.0    6860    2366    8.12    20.42                                   
17353   10000   580     315.39  121.0   3184.9  39.09   28.72   11.5    7703    2476    8.35    17.67                                   
;                                                                                                                                       
proc princomp out=prin ;  /*主成分分析模块*/                                                                                                              
var x1-x13;   /*要分析的指标*/                                                                                                                          
run;                                                                                                                                    
proc print data=prin;                                                                                                                   
var prin1-prin13;                                                                                                                             
run; 

相关系数矩阵

相关系数又称线性相关系数.它是衡量变量之间线性相关程度的指标。样本相关系数用r表示,总体相关系数用ρ表示,相关系数的取值范围为[-1,1]。|r|值越大，误差Q越小，变量之间的线性相关程度越高；|r|值越接近0，Q越大，变量之间的线性相关程度越低。

计算公式

Xk这里为指标，分别求得各个指标的均值X拔和标准差Sk。

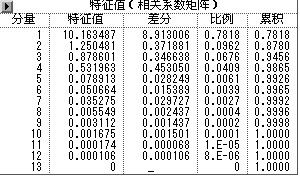
相关系数矩阵的特征值如下

AX=λX

每一个主成分所提取的信息量用方差来度量，每一个主成分方差的贡献等于原指标相关系数（对应特征向量）矩阵相应的特征值

从以上程序结果可以看出，第一、第二、第三主成分累计解释方差的比率已经超过了94%，所以只需要求λ1，λ2，λ3所对应的正交化特征向量。

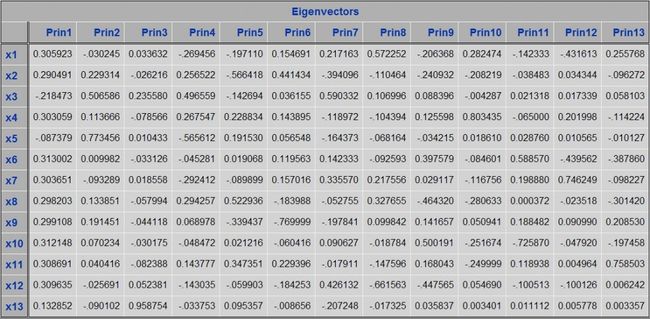
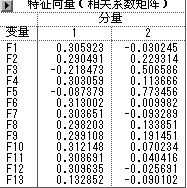
特征向量为

根据程序结果

F1=α1Y',F2=α2*Y',F3=α3*Y'

Y=[y1,y2,…,y13];

α1=(0.31,0.29,-0.25……0.13)

...

α3=(0.03,-0.03,0.24……0.96)

分析：前面三个主成分F1，F2，F3基本上反映了原来所有信息的94%，第一主成分与蔬菜种植面积（x1）、每公顷物质费用（x2）、蔬菜零售物价指数……等相关，表示的是市场经济综合因素，着重反映的是市场经济的成熟程度与国家现代化水平。

最后，可以计算三个主成分得分，并将其对应的方差比率作为权重，进行综合评价。

利用SAS Insight（交互式数据分析）做主成分分析

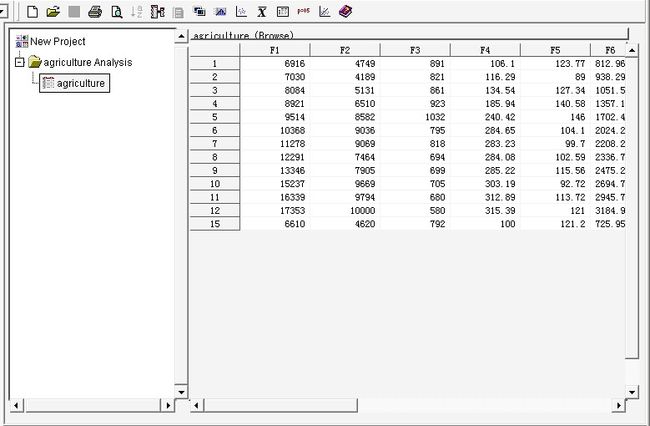
首先做好样本数据矩阵，每一行为一个观测值，每一列为一个指标，保存为数据集。这里设为Mylib.Agriculture。

命令行输入insight，（或选择交互式数据分析）启动insight模块，在insight模块中选择Mylib.Agriculture数据集。

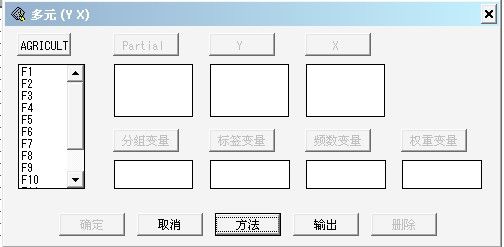
选择菜单分析|多元（YX），打开多元分析对话框

选择method方法按钮，

可以选择计算协方差矩阵的特征值或是相关系数矩阵的特征值，系统默认计算相关系数矩阵的特征值和特征向量，单击确定。 E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差，记作COV(X，Y)，即COV(X，Y)=E[(X-E(X))(Y-E(Y))]。

将主成分分析的变量x1-x13选为y变量，然后选择输出。

在弹出的多元对话框中包括“Descriptive Statistics（描述性统计量）”，"二变量图(BivariatePlots)"选项以及多种多元分析的选项，选中“主分量分析 Principal Component Analysis”复选框，单击主分量选项按钮，打开主分量选项对话框，选中特征向量复选框，取消相关结构（correlations structure）复选框

          

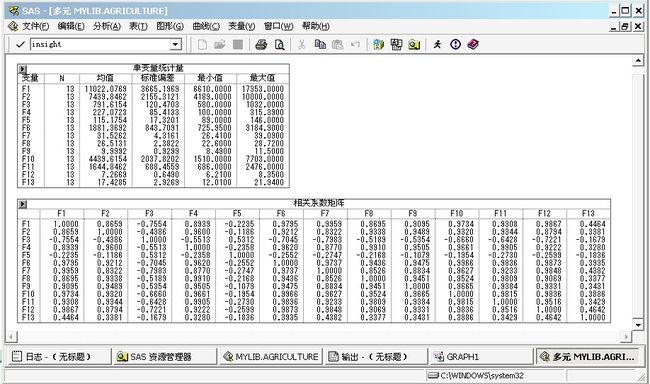
主成分结果分析

输出数字结果有4个部分，单变量统计量、相关系数矩阵、相关系数矩阵的特征值以及相关系数矩阵的特征向量。

特征值（Eigenvalue）、上下特征值之差（Difference）、各主成分的方差贡献率（Proportion）、以及累计（Cumulative）贡献率

前三个主成分的累计贡献率已达94.56%，只需前三个主成分就可以概括这组数据。前两个已经超出85%，因此给出了前两个。

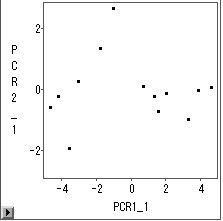
查看图表

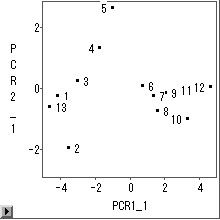
选择编辑|观察（observation）——>Label in Points(在图中添加标签)

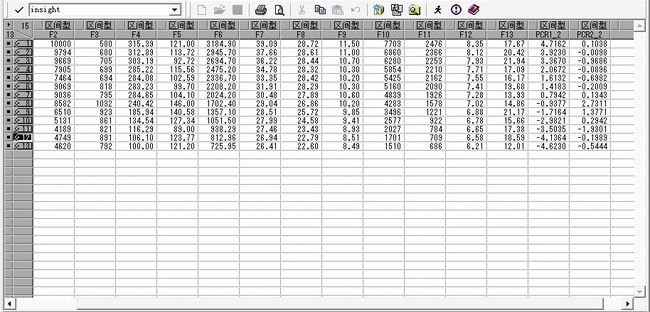
可以看到各个样本在两个主成分上的得分。

回到数据窗口可以看到前两个主成分的得分情况。右击数据窗口左上角的箭头，单击排序（sort）选项，选定排序变量PCR1，设为Des降序

可以据此进行比较。

使用分析家进行PCA分析

在表格上右键单击，选择文件|打开，找到sas数据文件，确定。

学则菜单，统计|多元分析，主成分分析，

在对话框中输入主成分分析的变量，单击统计按钮，打开主成分：统计。指定主成分的个数为4，

单击OK按钮。

单击SaveData按钮。选中Create and save scores data，单击OK返回。

单击Plots，选中碎石图和成分图