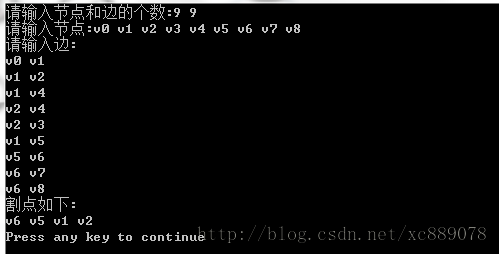
求一个连通图的割点，割点的定义是，如果除去此节点和与其相关的边，图不再连通，描述算法

参考：http://blog.csdn.net/cxllyg/article/details/7610265

 

题目：求一个连通图的割点，割点的定义是，如果除去此节点和与其相关的边，图不再连通，描述算法。

分析：

1. 最简单也是最直接的算法是，删除一个点然后判断连通性，如果删除此点，图不再连通，则此点是割点，反之不是割点（图的连通性一般通过深搜来判定，是否能一次搜索完 全部顶点）；

2. 通过深搜优先生成树来判定。从任一点出发深度优先遍历得到优先生成树，对于树中任一顶点Ｖ而言，其孩子节点为邻接点。由深度优先生成树可得出两类割点的特性：

     （１）若生成树的根有两棵或两棵以上的子树，则此根顶点必为割点。因为图中不存在连接不同子树顶点的边，若删除此节点，则树便成为森林；

     （２）若生成树中某个非叶子顶点V，其某棵子树的根和子树中的其他节点均没有指向V的祖先的回边，则V为割点。因为删去v，则其子树和图的其它部分被分割开来。

仍然利用深搜算法，只不过在这里定义visited[v]表示为深度优先搜索遍历图时访问顶点v的次序号，定义low[v]=Min{visited[v]，low[w]，visited[k]}，其中w是顶点v在深度优先生成树上的孩子节点；k是顶点v在深度优先生成树上由回边联结的祖先节点。

   割点判定条件：如果对于某个顶点v，存在孩子节点w且low[w]>=visited[v]，则该顶点v必为关节点。因为当w是v的孩子节点时，low[w]>=visited[v]，表明w及其子孙均无指向v的祖先的回边，那么当删除顶点v后，v的孩子节点将于其他节点被分割开来，从来形成新的连通分量。

 

#include <iostream>
#include <string>
using namespace std;

#define MAX_NUM 10

typedef struct EdgeNode
{
	int adjvex;
	struct EdgeNode *next;
}EdgeNode;

typedef struct VertexNode
{
	string data;
	EdgeNode *first;
}VertexNode,List[MAX_NUM];

typedef struct Graph
{
	List vertexnode;
	int num_vertex;
	int num_edge;
}Graph;

int count = 0;
int visit[MAX_NUM];
int low[MAX_NUM];

int get_location(Graph g, string s)
{
	for(int i=0;i<g.num_vertex;i++)
	{
		if(s == g.vertexnode[i].data)
			return i;
	}
	return -1;
}

void create_graph(Graph &g)//创建无向图
{
	int i,j,k;
	string s1,s2;
	cout<<"请输入节点和边的个数:";
	cin>>g.num_vertex>>g.num_edge;
	cout<<"请输入节点:";
	for(i=0;i<g.num_vertex;i++)
	{
		cin>>g.vertexnode[i].data;
		g.vertexnode[i].first=NULL;
	}
	cout<<"请输入边:"<<endl;
	for(k=0;k<g.num_edge;k++)
	{
		cin>>s1>>s2;
		i = get_location(g,s1);
		j = get_location(g,s2);

		EdgeNode *p = new EdgeNode();
		p->adjvex = j;
		p->next = g.vertexnode[i].first;
		g.vertexnode[i].first = p;

		EdgeNode *q = new EdgeNode();
		q->adjvex = i;
		q->next = g.vertexnode[j].first;
		g.vertexnode[j].first = q;
	}
}

void find_core(Graph g, int index)
{
	int min,w;
	EdgeNode *p;
	min = visit[index] = ++count;
	bool flag = false;

	for(p=g.vertexnode[index].first;p;p=p->next)
	{
		w = p->adjvex;
		if(visit[w]==0)
		{
			find_core(g,w);
			if(low[w] < min)
				min = low[w];
			else if(low[w] >= min)
			{
				if(flag == false)//防止重复打印
				{
					cout<<g.vertexnode[index].data<<" ";
					flag = true;
				}
			}
		}
		else if(visit[w] < min)
		{
			min = visit[w];
		}
	}
	low[index]=min;
}

void find(Graph g)
{
	int i;
	for(i=0;i<MAX_NUM;i++)
	{
		visit[i]=0;
		low[i]=65536;
	}
	visit[0] = 1;//从v0出发
	low[0] = 1;
	count=1;
	EdgeNode *p = g.vertexnode[0].first;
	int index = p->adjvex;
	find_core(g,index);
	if(count < g.num_vertex)//v0至少有两个子图
	{
		cout<<g.vertexnode[0].data<<" ";//v0是一个割点
		p = p->next;
		while(p)//遍历其它的子图
		{
			index = p->adjvex;
			if(visit[index]==0)
				find_core(g,index);
			p = p->next;
		}
	}
}

int main()
{
	Graph g;
	create_graph(g);
	cout<<"割点如下:"<<endl;
	find(g);
	cout<<endl;
	return 0;
}