How to use libsvm for regression in matlab (It is very important)
Website: http://www.ece.umn.edu/users/cherkass/ee4389/SVR.html
Parameters
% options:
% -s svm_type : set type of SVM (default 0)
% 0 -- C-SVC
% 1 -- nu-SVC
% 2 -- one-class SVM
% 3 -- epsilon-SVR
% 4 -- nu-SVR
% -t kernel_type : set type of kernel function (default 2)
% 0 -- linear: u'*v
% 1 -- polynomial: (gamma*u'*v + coef0)^degree
% 2 -- radial basis function: exp(-gamma*|u-v|^2)
% 3 -- sigmoid: tanh(gamma*u'*v + coef0)
% -d degree : set degree in kernel function (default 3)
% -g gamma : set gamma in kernel function (default 1/num_features)
% -r coef0 : set coef0 in kernel function (default 0)
% -c cost : set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)
% -n nu : set the parameter nu of nu-SVC, one-class SVM, and nu-SVR (default 0.5)
% -p epsilon : set the epsilon in loss function of epsilon-SVR (default 0.1)
% -m cachesize : set cache memory size in MB (default 100)
% -e epsilon : set tolerance of termination criterion (default 0.001)
% -h shrinking: whether to use the shrinking heuristics, 0 or 1 (default 1)
% -b probability_estimates: whether to train a SVC or SVR model for probability estimates, 0 or 1 (default 0)
% -wi weight: set the parameter C of class i to weight*C, for C-SVC (default 1)
% -v n: n-fold cross validation mode % the older version does not the cross validation
% -q : quiet mode (no outputs) % the older version does not this opearation
Description
This section describes application of the SVM Regression software provided in the LibSVM software package. The MATLAB interface for LibSVM is available in the package. Standard SVM Regression (SVR) formulation is referred to as epsilon-SVR in this package. The package also includes other versions of SVR; however only the epsilon-SVR option is described below.
There are two main interfaces in this package:
-
svmtrain
-
svmpredict
Usage interface svmtrain
This interface is used to train the SVM regression model.
model = svmtrain(trnY, trnX, param)
Input arguments
- trnY
-
This is a dimensional vector of the training data response values,
where is the total number of samples. - trnX
-
This is a
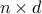 dimensional training data input matrix,
dimensional training data input matrix,
where is the total number of samples and is the number of features for each sample.
is the number of features for each sample.
Tunable parameters
- param
-
This is a string which specifies the model parameters.
For Regression, a typical parameter string may look like, ‘-s 3 -t 2 -c 20 -g 64 -p 1’ where
-
-s svm type, 3 for epsilon-SVR
-
-t kernel type, 2 for radial basis function
-
-c cost parameter
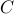 of epsilon-SVR
of epsilon-SVR -
-g width parameter
 for RBF kernel
for RBF kernel -
-p for epsilon-SVR
Check LibSVM for a detailed description of other options.
Output
- model
-
This is the trained SVM model providing predicted response values for test inputs.
Usage interface svmpredict
This interface is used to test the SVM regression model.
[y_hat, Acc] = svmpredict(tstY, tstX, model)
Input arguments
- tstY
-
This is a dimensional vector of the test data response values,
where is the total number of samples. - tstX
-
This is a
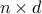 dimensional test data input matrix,
dimensional test data input matrix,
where is the total number of samples and is the number of features for each sample.
is the number of features for each sample. - model
-
This is the trained SVM model obtained using the svmtrain interface,
which can be used to obtain the prediction outputs on a test data sample.
Output
- y_hat
-
This is the dimensional predicted response value of the test data samples tstX.
- Acc
-
This is the mean squared error for the test data.
Example
This example uses the ‘motorcycle’ data introduced with the XTAL package. We illustrate the use of SVM regression with a RBF kernel.
tmp = load('xtal_linuxtrain.txt', '-ascii');
trn_data.X = tmp(:,1)';
trn_data.y = tmp(:,2);
tmp = load('xtal_linuxtest.txt', '-ascii');
tst_data.X = tmp(:,1)';
tst_data.y = tmp(:,2);
[trn_data, tst_data, jn2] = scaleSVM(trn_data, tst_data, trn_data, 0, 1);
Note, for this example we set ![]() to a constant value as prescribed in Equation 9.61 of the book. Further, we perform model selection for and
to a constant value as prescribed in Equation 9.61 of the book. Further, we perform model selection for and ![]() using 5-fold cross validation.
using 5-fold cross validation.
param.s = 3; % epsilon SVR param.C = max(trn_data.y) - min(trn_data.y); % FIX C based on Equation 9.61 param.t = 2; % RBF kernel param.gset = 2.^[-7:7]; % range of the gamma parameter param.eset = [0:5]; % range of the epsilon parameter param.nfold = 5; % 5-fold CV Rval = zeros(length(param.gset), length(param.eset)); for i = 1:param.nfold % partition the training data into the learning/validation % in this example, the 5-fold data partitioning is done by the following strategy, % for partition 1: Use samples 1, 6, 11, ... as validation samples and % the remaining as learning samples % for partition 2: Use samples 2, 7, 12, ... as validation samples and % the remaining as learning samples % : % for partition 5: Use samples 5, 10, 15, ... as validation samples and % the remaining as learning samples data = [trn_data.y, trn_data.X]; [learn, val] = k_FoldCV_SPLIT(data, param.nfold, i); lrndata.X = learn(:, 2:end); lrndata.y = learn(:, 1); valdata.X = val(:, 2:end); valdata.y = val(:, 1); for j = 1:length(param.gset) param.g = param.gset(j); for k = 1:length(param.eset) param.e = param.eset(k); param.libsvm = ['-s ', num2str(param.s), ' -t ', num2str(param.t), ... ' -c ', num2str(param.C), ' -g ', num2str(param.g), ... ' -p ', num2str(param.e)]; % build model on Learning data model = svmtrain(lrndata.y, lrndata.X, param.libsvm); % predict on the validation data [y_hat, Acc, projection] = svmpredict(valdata.y, valdata.X, model); Rval(j,k) = Rval(j,k) + mean((y_hat-valdata.y).^2); end end end Rval = Rval ./ (param.nfold);
[v1, i1] = min(Rval); [v2, i2] = min(v1); optparam = param; optparam.g = param.gset( i1(i2) ); optparam.e = param.eset(i2);
Based on the minimum validation error, the best model is (from Equation 9.61). ![]() and
and ![]() .
.
| |
|
|
|
|
||
| |
2382.267 | 2376.982 | 2391.682 | 2402.548 | 2412.888 | 2432.055 |
| |
2313.489 | 2320.621 | 2333.430 | 2323.429 | 2312.017 | 2303.053 |
| 2210.922 | 2197.156 | 2187.927 | 2181.607 | 2170.894 | 2146.244 | |
| |
1928.355 | 1919.255 | 1916.538 | 1912.344 | 1895.023 | 1900.917 |
| |
1649.516 | 1641.646 | 1638.431 | 1625.665 | 1615.502 | 1614.951 |
| |
1160.306 | 1154.952 | 1152.771 | 1147.345 | 1163.053 | 1171.488 |
| |
857.4170 | 863.7603 | 863.4076 | 859.5823 | 857.9985 | 849.2161 |
| |
681.7371 | 672.0156 | 668.4148 | 672.9413 | 679.2028 | 697.0018 |
| |
678.1910 | 679.3564 | 685.1602 | 679.2798 | 681.5483 | 684.1367 |
| |
702.7702 | 701.1718 | 698.7076 | 692.9010 | 703.4782 | 703.2296 |
optparam.libsvm = ['-s ', num2str(optparam.s), ' -t ', num2str(optparam.t), ... ' -c', num2str(optparam.C), ' -g ', num2str(optparam.g), ... ' -p ', num2str(optparam.e)]; model = svmtrain(trn_data.y, trn_data.X, optparam.libsvm);
% MSE for test samples [y_hat, Acc, projection] = svmpredict(tst_data.y, tst_data.X, model); MSE_Test = mean((y_hat-tst_data.y).^2); NRMS_Test = sqrt(MSE_Test) / std(tst_data.y); % MSE for training samples [y_hat, Acc, projection] = svmpredict(trn_data.y, trn_data.X, model); MSE_Train = mean((y_hat-trn_data.y).^2); NRMS_Train = sqrt(MSE_Train) / std(trn_data.y);
The performance of the selected (final) model is
| MSE | NRMS | |
| Training | 554.7569 | 0.4698 |
| Test | 356.95 | 0.4362 |
X = 0:0.01:1;
X = X';
y = ones(length(X), 1);
y_est = svmpredict(y, X, model);
h = plot(trn_data.X, trn_data.y, 'ko', tst_data.X, tst_data.y, 'kx', X, y_est, 'r--');
legend('Training', 'Test', 'Model');
y1 = max([trn_data.y; tst_data.y]);
y2 = min([trn_data.y; tst_data.y]);
axis([0 1 y2 y1]);
 |