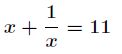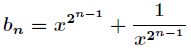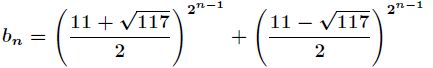关于欧拉工程的一道递推题
今天来讲的是在欧拉工程上的一道递推题,题目描述如下链接。
题目:https://projecteuler.net/problem=492
当然,这道题在51Nod上有一个比较通用的版本,链接如下
题目:http://www.51nod.com/contest/problem.html#!problemId=1361
题意:给定![]() ,并且有,给定两个数
,并且有,给定两个数![]() 和
和![]() ,求
,求![]() 的值。其中
的值。其中
满足![]() 和,并且
和,并且![]() 为素数。
为素数。
分析:首先对原递推式进行变换得到
![]()
那么令,继而有![]() ,而。到了这里,假设
,而。到了这里,假设
那么我们带入继续递推会发现一个神奇的结论
其中假设取其中一个解如下
那么得到![]() 如下
如下
好了,到了这里,最直观的做法就是根据上述公式求出![]() ,然后会带回去求出即可。
,然后会带回去求出即可。
如果想用二次剩余的方法来做,因为可能无解,所以不能用这种方法做。看成更一般
形式的求解,比如下面
那么回忆之前的一篇文章:http://blog.csdn.net/acdreamers/article/details/8994222,重
点是HDU4565题,这是明显可以构造矩阵的,具体如何构造不再赘述。然后先得到递推式如下
所以最终得到![]() 如下
如下
可以看到矩阵的指数很大,所以需要降小,而这是一个经典的矩阵找寻环节问题。之前有篇文章,如下
链接:http://blog.csdn.net/acdreamers/article/details/25616461
当时那道题由于要求最小的循环节,所以要求比较精确,必须枚举因子。但是对于本题不同,我们只要能
求出一个合理的循环节即可,不要求最小的,因为不影响最终结果。
参照当时的结论,由于117不是素数,所以只有两种情况。
(1)如果117是![]() 的二次剩余时,最小循环节是的因子,我们可以取作为循环节。
的二次剩余时,最小循环节是的因子,我们可以取作为循环节。
(2)如果117是![]() 的二次非剩余时,最小循环节是的因子,可以取作
的二次非剩余时,最小循环节是的因子,可以取作
为循环节。
到了这里大部分问题都已经解决。实际上当117是![]() 的二次非剩余时,循环节可以为
的二次非剩余时,循环节可以为![]() ,至于为什么是
,至于为什么是
正确的,请来个大神证明! 另外![]() 为2或者3时,需要特判。
为2或者3时,需要特判。
代码:
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
typedef long long LL;
const int N = 2;
struct Matrix
{
LL m[N][N];
};
Matrix I =
{
1, 0,
0, 1
};
LL quick_mod(LL a, LL b, LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
LL Legendre(LL a, LL p)
{
LL t = quick_mod(a, (p - 1) >> 1, p);
if(t == 1) return 1;
return -1;
}
Matrix multi(Matrix a, Matrix b, LL m)
{
Matrix c;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
{
c.m[i][j] = 0;
for(int k = 0; k < N; k++)
c.m[i][j] += a.m[i][k] * b.m[k][j] % m;
c.m[i][j] %= m;
}
}
return c;
}
Matrix power(Matrix A, LL k, LL m)
{
Matrix ans = I, p = A;
while(k)
{
if(k & 1)
{
ans = multi(ans, p, m);
k--;
}
k >>= 1;
p = multi(p, p, m);
}
return ans;
}
LL GetLoop(LL p)
{
if(Legendre(117, p) == -1)
return p + 1;
return p - 1;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
LL n, p;
scanf("%lld %lld", &n, &p);
if(p == 2 || p == 3)
{
puts("1");
continue;
}
Matrix A;
A.m[0][0] = 11 % p;
A.m[0][1] = p - 1;
A.m[1][0] = 1;
A.m[1][1] = 0;
LL loop = GetLoop(p);
LL x = quick_mod(2, n - 1, loop);
x = ((x - 1) % loop + loop) % loop;
Matrix ans = power(A, x, p);
LL res = (ans.m[1][0] * 119 % p + ans.m[1][1] * 11 % p) % p;
res = ((res - 5) % p + p) % p;
res = res * quick_mod(6, p - 2, p) % p;
printf("%lld\n", res);
}
return 0;
}