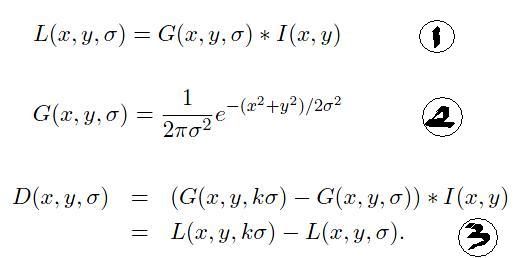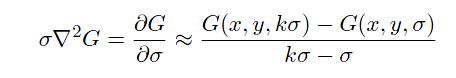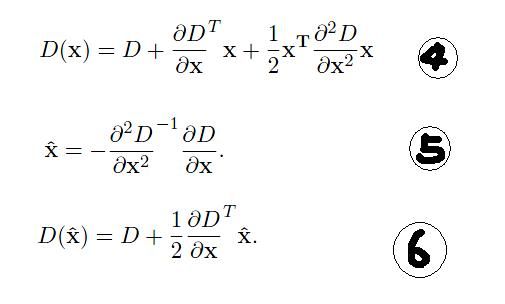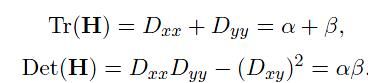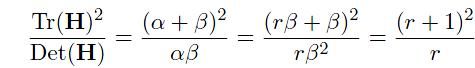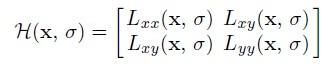SIFT,SURF和PCA-SIFT对比
本文转自:http://www.cnblogs.com/blue-lg/archive/2012/07/17/2594868.html
http://www.cnblogs.com/mysunnyday/archive/2011/08/31/2160298.html
更详尽内容可参考:
SIFT特征提取分析:http://blog.csdn.net/abcjennifer/article/details/7639681
特征提取方法 SIFT,PCA-SIFT,GLOH,SURFhttp://blog.csdn.net/abcjennifer/article/details/7681718
图像特征提取、描述、匹配综合篇:http://blog.csdn.net/sangni007/article/category/1306968
Ⅰ、图像匹配算法研究之sift算法
SIFT算法由D.G.Lowe 1999年提出,2004年完善总结,论文发表在2004年的IJCV上,主要用于提取具有图像旋转不变性和伸缩不变性的特征点。
这项技术可以推广到图像识别、图像拼接以及图像恢复等。
David G. Lowe, "Distinctive image features from scale-invariant keypoints," International Journal of Computer Vision, 60, 2 (2004), pp. 91-110
论文详细地址:lowe sift算法
算法主要分为4个步骤:
- scale-space extrema detection--尺度空间上的极值检测
- keypoint localization--关键点的定位
- orientation assignment --为关键点标定方向
- keypoint descriptor--提取特征点描述符
$1. 尺度空间上的极值检测
在介绍这一部分的时候,先引入几个概念:
- 降采样:对于一幅图像而言的降采样就是每隔几行、几列得到取一点,组成一个新的图像。以比例因子为2的降采样来说:就是対一幅图像每隔一行一列取一点。
- 升采样:其实一种插值,就是在一幅图像里利用相关的插值运算得到一幅大的图像!比如比例因子为2的升采样就是每个相邻像素点种插值出一个像素(这里包括X、Y两个方向),最常用的插值方法有线性插值等。
- 图像金字塔:由一个原始图像经过降采样得到一幅图像,再对新的图像做降采样,重复多次构成的一组集合。以采样因子2为例说明,如果形象的把这些图像摞起来就想一个金字塔,每次之间长和宽大小恰好为2倍关系,故此得名。
- 高斯卷积:就是权函数为高斯函数的模板进行卷积运算。通常做高斯卷积后的图像会比原图像平滑但也会模糊,所以又称高斯模糊!
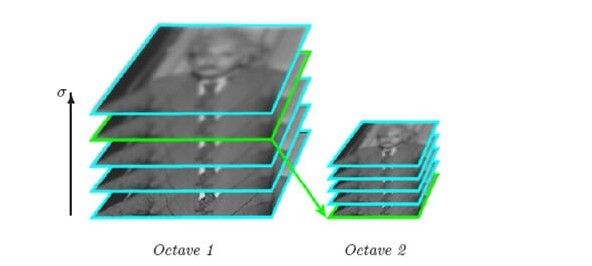
- 高斯金字塔:高斯金字塔里有两个概念:组(Octave)和层(Level或Interval),每组里有若干层!高斯金字塔的构造是这样的,第一组的第一层为原图像,然后将图像做一次高斯平滑(高斯卷积、高斯模糊)高斯平滑里有一个参数δ,在SIFT里作者取1.6 。然后将δ乘一个比例系数k作为新的平滑因子来平滑第一组第二层得到第三层,重复若干次,得到L层(L一般取5)他们分别对应的平滑参数为:0,δ,kδ,k2δ,k3δ。然后将最后一幅图像做比例因子为2的降采样得到第二组的第一层,然后对第二组的第一层做参数是δ的高斯平滑,对第二层做kδ的平滑得到第三层.....这里一定注意:每组对应的平滑因子δ是一样的,而不是像有的资料上说的持续递增。这样反复形成了O组L层的高斯金字塔。一般模糊的高斯模板长宽都约为6δ(这里δ为当次的平滑因子,就是可能是kδ,k2δ..)
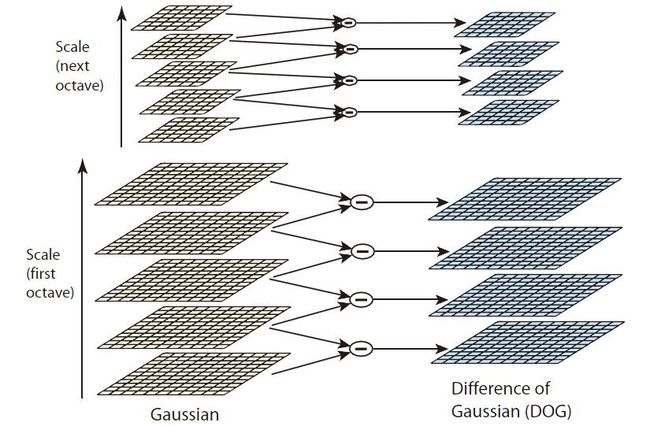
- DoG(Difference of Gaussian)金字塔:是由高斯金字塔构造出来的,他的第一组第一层是由高斯金字塔的第一组第二层减第一组第一层,他的第一组第二层是由高斯金字塔的第一组第三层减第一组第二层得到。每组都这样就生成了一个DoG金字塔。顺便说一下,DoG金字塔每组图像几乎都是一片黑,但仔细看你能看出轮廓的。
最后关于金字塔具体处理的说明:
1)在SIFT里高斯金字塔的第一组第一层通常是由一个原图像长宽扩大一倍开始的,这样做是为了可以得到更多的特征点 ;
2)大家可以发现如果用每组5层的高斯金字塔构造一个DoG金字塔的的话,DoG的每组的层数是4 ;
3)对于DoG金字塔,特征点的搜索从每组的二层到倒数第二层的(后面说明为什么),所以如果DoG金字塔有效层数目为n的话,那么DoG金字塔应该有n+2层,那么对 应的高斯金字塔应该有n+3层 ;
4)高斯金字塔从第二组开始的每组第一层是由上一组的倒数第二层降采样得到的,如下所示。
讲了这么多概念,现在正式开始讲解如何在尺度空间里寻找特征点啦。
由于图像进行伸缩等变换后尺度空间发生变化,所以为了方便找出匹配点,需要将图像在不同的尺度空间里进行平滑,并相减得到更多的边缘等高频信息(特征点的集中 域)。高斯平滑并计算dog金字塔利用下面的3个计算公式:
至于为什么用DOG算子来提取额特征点,而不是hessian或者其他角点方法比如Harris,是因为Mikolajczyk (2002)发现通过
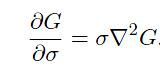 计算出来的局部区域极大值和极小值与上述几种角点相比能产生更加稳定的特征点。
计算出来的局部区域极大值和极小值与上述几种角点相比能产生更加稳定的特征点。
但是上面的公式和DOG又有素描关系呢?看下面的公式就知道了:
两者之间只是相差了(k-1)δ2 倍而已,不影响特征点的寻找。
还有一点需要说明的是,这里不同的δ就是代表不同的尺度,0(本身),δ,kδ,等等... δ的值越大,意味着尺度空间越大。具体该怎么理解尺度这个概念呢,就是需要描述的像素灰度分布越广,尺度越广,也就是说越模糊的图像尺度也越大。举个例子,有两个灰度值分别为0和1,模糊后变为0.4和0.6,要表示这两个灰度值需要更多的参数,尺度变大。更简单的说尺度就是频率,高斯模糊越明显,尺度越大,因为这时图像是低频的。
剩下的只需要在DOG金字塔里寻找3X3X3邻域的极值即为我们所要寻找的feature points.如下图所示,
$2. 关键点的精确定位
通过拟和三维二次函数以精确确定关键点的位置和尺度(达到亚像素精度),同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应),以增强
匹配稳定性、提高抗噪声能力。
①空间尺度函数泰勒展开式如(4 )所示:
对(4)求导,并令其为0,得到精确的位置(5)。
②在已经检测到的特征点中,要去掉低对比度的特征点和不稳定的边缘响应点。去除低对比度的点:把公式(5)代入公式(4),可得(6)。
若(6)的值大于0.03 ,该特征点就保留下来,否则丢弃。
③边缘响应的去除
一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率,而在垂直边缘的方向有较小的主曲率。主曲率通过一个2×2 的Hessian矩阵H求出:
导数由采样点相邻差估计得到。D的主曲率和H的特征值成正比,令α为最大特征值,β为最小的特征值,则
令α=rβ 则:
(r + 1)2/r的值在两个特征值相等的时候最小,随着r的增大而增大,因此,为了检测主曲率是否在某域值r下,只需检测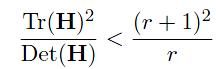 。
。
在Lowe的文章中,取r=10。
$3. 关键点方向分配
利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性。
梯度大小和方向计算公式如下:
orientation histogram的生成,将0~360度分到36个区间中,每个区间的高度计算如下:∑m(xi,yi)*g(x0,y0,1.5δ) 其中δ为当前的尺度,(x0,y0)为当前特征点的坐标而g(x0,y0,1.5δ)则是高斯滤波系数,计算公式➹(2)。
主方向定义为拥有最高峰hm的那个区间,而其他区间高度为0.8*hm之上的区间方向可以认为是该特征点的辅方向,这样就增强了匹配的鲁棒性。
这样,每个关键点key points就有三个信息:位置(x0,y0)、所处尺度δ、方向。
若表示出来,效果如下:
图1
$4. 提取特征描述子
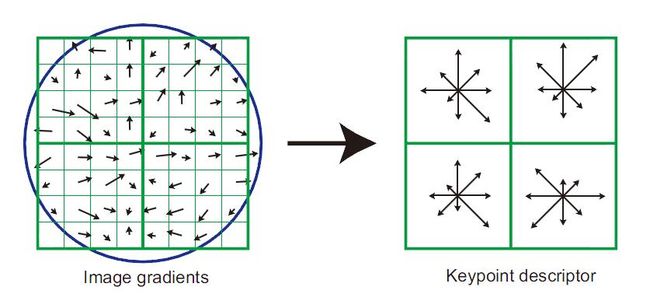
图2
- 首先将坐标轴旋转为关键点的方向,以确保旋转不变性;
- 为了方便起见,在$3部分利用公式7计算梯度时,应该计算全体像素点的梯度方向及大小;
- lowe建议选取16X16邻域,然后将这个大区域分为16个4X4区域,再分别对每个区域中16个像素点的梯度大小乘上高斯模板系数(此时的δ为0.5*4=2);
- 将16个单位方向向量按照常规的8方向分布,并乘上上一步计算的幅值叠加起来,得到类似图2右边的效果。
最后,一共有4X4X8=128维向量来表征这个特征点。
此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响,再继续将特征向量的长度归一化,则可以进一步去除光照变化的影响。
$5. 后续匹配工作
当两幅图像的SIFT特征向量生成后,下一步我们采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图像1中的某个关键点,并找
出其与图像2中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离少于某个比例阈值,则接受这一对匹配点。降低这个比例阈值,
SIFT匹配点数目会减少,但更加稳定。为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点。Lowe提出了比较最近邻距离与次近邻距离的方法,距离比率
ratio小于某个阈值的认为是正确匹配。因为对于错误匹配,由于特征空间的高维性,相似的距离可能有大量其他的错误匹配,从而它的ratio值比较高。Lowe推荐ratio的
阈值为0.8。但作者对大量任意存在尺度、旋转和亮度变化的两幅图片进行匹配,结果表明ratio取值在0. 4~0. 6之间最佳,小于0. 4的很少有匹配点,大于0. 6的则
存在大量错误匹配点。作者建议ratio的取值原则如下:
ratio=0. 4 对于准确度要求高的匹配;
ratio=0. 6 对于匹配点数目要求比较多的匹配;
ratio=0. 5 一般情况下。
也可按如下原则:当最近邻距离<200时ratio=0. 6,反之ratio=0. 4。ratio的取值策略能排分错误匹配点。
至此,整个sift算法完毕。
-
Ⅱ、图像匹配算法研究之surf算法
SURF意指 加速的具有鲁棒性的特征,由Bay在2006年首次提出,这项技术可以应用于计算机视觉的物体识别以及3D重构中。SURF算子由SIFT算子改进而来,一般来说,标准的SURF算子比SIFT算子快好几倍,并且在多幅图片下具有更好的鲁棒性。SURF最大的特征在于采用了harr特征以及积分图像integral image的概念,这大大加快了程序的运行时间。
surf提出算法参见http://www.vision.ee.ethz.ch/~surf/papers.html 有paper下载地址。
1、提取特征点
2、提取特征描述符
- 1. 特征点的提取
1)利用Hessian矩阵,计算特征值α
其中Lxx(x, σ)是高斯滤波后图像g(σ)的在x方向的二阶导数,其他的Lyy(x, σ)、Lxy(x, σ)都是g(σ)的二阶导数。
为了减小计算量,原文使用了一个简单的方法,并利用了积分图像的优势(大大的减少计算量),方法其实很简单就是在模糊的基础上将原本的模块近似下。
总所周知,一般计算图像的二阶导时,利用下面的公式d2f(x)/dx2=(f(x+1)-f(x))-(f(x)-f(x-1))=-2*f(x)+f(x+1)+f(x-1)。但是f(x)=g(h(x))【h(x)为图像的灰度值,f(x)
是将h(x)高斯滤波处理的灰度函数 】
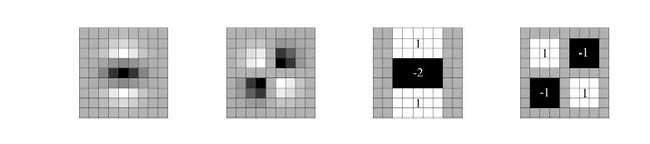
图一 模板近似
以9X9滤波器为例,如上图所示,左边两幅图分别为灰度图像在中心点(黑色点)处的二阶导数d2f(x)/dx2和d2f(x)/dxdy的模板对应的值, 近似后变成右边的两幅图,图中灰色部分像素值为0。可是这样计算特征值不是也很复杂么?当然,所以作者提供了一种新思路--使用积分图像。
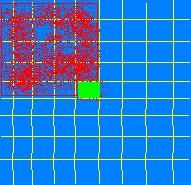
积分图像,顾名思义,即指当前像素点所在位置距原点(0,0)所包围面的所有灰度之和。
绿色的部分为当前像素点,红色为积分区域。
这样计算图像中任意一块矩形区域的灰度之和Sx只需要利用矩形4个顶点(Xi,Yi)(i=1,2,3,4 顺序为从上之下,先左后右)的积分值S(x,y)即可。
Sx=S(X1,Y1)+S(X4,Y4)-S(X2,Y2)-S(X3,Y3)
至此,大家应该知道近似二阶导数的高斯模板并引入积分图像的好处了吧,只需要在函数定义之前计算各个坐标点的积分图像,然后就能方便的求出hessian的特征值。
不过由于函数模板的近似,这里需要修正下特征值α的求解公式:
这里Dxx和Dxy就是根据图一得到的,而Dyy和Dxx类似,只需要导致一下模板即可。
2)根据是否为领域极大值判断特征点
这里要引入图像堆的概念,说简单点,就是一组大小相同的图像,这些图像都是根据不同大小高斯滤波二阶导模板,如图一所示 得到的平滑后图像Pi 。
按照模板大小从小到大将Pi沿z轴方向排布,这样中间层的每个像素点的领域就为3X3X3(包括上下两层)。若该点的特征值α为这27个点中的最大值,那么可以认为该点为Feature points--特征点(图像依据这些特征点的匹配进行更多的操作,比如拼接,比较相似性等等)。
- 2.特征点的匹配
1)寻找特征向量
欲进行特征点的匹配,必须提取出特征点的特征向量再利用两个向量的相似程度认为两个点是否为两幅图像相互对应的点。
第一步.计算特征点的主方向
以特征点为圆心半径为6像素建立圆领域,计算得出里面有109个像素点。计算这些点的harr特征harrx和harry.
那么该怎样计算任意一点的harr特征值?
图二 harr-like特征
选取edge features前两个作为harrx和harry值,这个方向有些类似与梯度方向,不过这里的领域显然更广。至于计算么,依旧是利用积分图像。
对这109个像素点分别求出各自的向量的方向angle=acrtan(harry/harrx) ,根据最近邻原则将这些 angle划分到60,120,...,300,360等6个值上。划分在同一范围上的像素点分别将他们的harrx和harry相加即可。不过为了体现相邻像素点的更大影响,还需要考虑高斯权重系数。这样得到最大的harrx和最大的harry,组成了主方向向量。
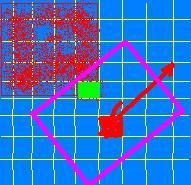
第二步.提取特征描述符
图中红色箭头为上面计算出来的主方向,按上图所示选取该红色特征点的8X8邻域(紫色边框内部)
计算得到4X4个像素块的梯度大小和方向(可以利用上面已经计算的harrx和harry),将8X8区域分割为2X2个区域T1,2,3,4,这样每个区域就包括了4个更小的由4个像素点组成的区域,
| x1 | x2 |
| x3 | x4 |
harrx和harry就是利用白色部分像素灰度值减去黑色部分像素灰度值即可得到(harrx,harry)方向向量。这样的向量一共有16个,将这些方向向量的方向角归并到上下左右斜上下8个方向上,并在T1,2,3,4中计算这8个方向的值。
那么这个4X8=32维向量即为所求的特征描述符。
3)特征点的匹配
采用最简单的两向量内积最大值为最匹配的点,设定一阈值,只有当这个最大值大于该阈值方可认为两特征点匹配。
至此,surf算法结束。
-
Ⅲ、SURF与SIFT比较
共同点:
SIFT/SURF为了实现不同图像中相同场景的匹配,主要包括三个步骤:
1、尺度空间的建立;
2、特征点的提取;
3、利用特征点周围邻域的信息生成特征描述子
4、特征点匹配。
从博客上看到一片文章,http://blog.csdn.net/cy513/archive/2009/08/05/4414352.aspx,这一段的大部分内容源于这篇文章,推荐大家去看看。
如果两幅图像中的物体一般只是旋转和缩放的关系,加上图像的亮度及对比度的不同,要在这些条件下要实现物体之间的匹配,SIFT算法的先驱及其发明者想到只要找到多于三对物体间的匹配点就可以通过射影几何的理论建立它们的一一对应。
如何找到这样的匹配点呢?SIFT/SURF作者的想法是首先找到图像中的一些“稳定点”,这些点是一些特殊的点,不会因为视角的改变、光照的变化、噪音的干扰而消失,比如角点、边缘点、暗区域的亮点以及亮区域的暗点。这样如果两幅图像中有相同的景物,那么这些稳定点就会在两幅图像的相同景物上同时出现,这样就能实现匹配。因此,SIFT/SURF算法的基础是稳定点。
SIFT/SURF提取的稳定点,首先都要求是局部极值。但是,当两个物体的大小比例不一样时,大图像的局部极值点在小图像的对应位置上有可能不是极值点。于是SIFT/SURF都采用图像金字塔的方法,每一个截面与原图像相似,这样两个金字塔中就有可能包含大小最近似的两个截面了。
这样找到的特征点会比较多,经过一些处理后滤掉一些相对不稳定的点。
接下来如何去匹配相同物体上对应的点呢?SIFT/SURF的作者都想到以特征点为中心,在周围邻域内统计特征,将特征附加到稳定点上,生成特征描述子。在遇到旋转的情况下,作者们都决定找出一个主方向,然后以这个方向为参考坐标进行后面的特征统计,就解决了旋转的问题。
共同的大问题有以下几个:
1、为什么选用高斯金字塔来作特征提取?
为什么是DOG的金字塔?因为它接近LOG,而LOG的极值点提供了最稳定的特征,而且DOG方便计算(只要做减法。)
为什么LOG的极值点提供的特征最稳定,有参考文献,未看。
(7.12补充:)直观理解:特征明显的点经过不同尺度的高斯滤波器进行滤波后,差别较大,所以用到的是DOG。
但是直观上怎么理解?如果相邻Octave的sigma不是两倍关系还好理解:如果两幅图像只是缩放的关系,那么假设第一个Octave找到了小一倍图像的极值点,那么大一倍图像的极值点会在下一个Octave找到相似的。但是现在,如果把大一倍图像进行一次下采样(这样和小的图像就完全一样了),进行Gauss滤波时,两个图像滤波系数(sigma)是不一样的,不就找不到一样的极值点了么?不理解。
2、Hessian矩阵为什么能用来筛选极值点?
SIFT先利用非极大抑制,再用到Hessian矩阵进行滤除。SURF先用Hessian矩阵,再进行非极大抑制。SURF的顺序可以加快筛选速度么?(Hessian矩阵滤除的点更多?)
至于SURF先用Hessian矩阵,再进行非极大抑制的原因,是不管先极大值抑制还是判断Hessian矩阵的行列式,金字塔上的点的行列式都是要计算出来的。先判断是否大于0只要进行1次判断,而判断是否是极大值点或者极小值点要与周围26个点比较,只比较1次肯定快。
而在SIFT中,构建的高斯金字塔只有一座(不想SURF是有3座),要进行非极大抑制可以直接用金字塔的结果进行比较。而如果计算Hessian矩阵的行列式,还要再计算Dxx、Dxy、Dyy。因此先进行非极大抑制。这两个步骤的先后与SIFT/SURF的实际计算情况有关的,都是当前算法下的最佳顺序,而不是说哪种先计算一定更好。
3、为什么采用梯度特征作为局部不变特征?
这与人的视觉神经相关。采用梯度作为描述子的原因是,人的视觉皮层上的神经元对特定方向和空间频率的梯度相应很敏感,经过SIFT作者的一些实验验证,用梯度的方法进行匹配效果很好。
4、为什么可以采用某些特征点的局部不变特征进行整幅图像的匹配?
我在一份博客上找到这样一句话:(http://apps.hi.baidu.com/share/detail/32318290,大家可以看看这篇文章。)
从直观的人类视觉印象来看,人类视觉对物体的描述也是局部化的,基于局部不变特征的图像识别方法十分接近于人类视觉机理,通过局部化的特征组合,形成对目标物体的整体印象,这就为局部不变特征提取方法提供了生物学上的解释,因此局部不变特征也得到了广泛应用。
还有:
图像中的每个局部区域的重要性和影响范围并非同等重要,即特征不是同等显著的,其主要理论来源是Marr的计算机视觉理论和Treisman的特征整合理论,一般也称为“原子论”。该理论认为视觉的过程开始于对物体的特征性质和简单组成部分的分析,是从局部性质到大范围性质。
SIFT/SURF都是对特征点的局部区域的描述,这些特征点应该是影响重要的点,对这些点的分析更加重要。所以在局部不变特征的提取和描述时也遵循与人眼视觉注意选择原理相类似的机制,所以SIFT/SURF用于匹配有效果。
不同点的比较:
从博客上看到一个总结,我修改了一些内容。大家可以参看以下链接:
http://blog.csdn.net/ijuliet/archive/2009/10/07/4640624.aspx
|
|
SIFT |
SURF |
| 尺度空间 |
DOG与不同尺度的图片卷积 |
不同尺度的box filters与原图片卷积 |
| 特征点检测 |
先进行非极大抑制,再去除低对比度的点。再通过Hessian矩阵去除边缘的点 |
先利用Hessian矩阵确定候选点,然后进行非极大抑制 |
| 方向 |
在正方形区域内统计梯度的幅值的直方图,找max对应的方向。可以有多个方向。 |
在圆形区域内,计算各个扇形范围内x、y方向的haar小波响应,找模最大的扇形方向 |
| 特征描述子 |
16*16的采样点划分为4*4的区域,计算每个区域的采样点的梯度方向和幅值,统计成8bin直方图,一共4*4*8=128维 |
20*20s的区域划分为4*4的子区域,每个子区域找5*5个采样点,计算采样点的haar小波响应,记录∑dx, ∑dy,∑|dx|,∑|dy|,一共4*4*4=64维 |
SURF—金字塔仅仅是用来做特征点的检测。在计算描述子的时候,haar小波响应是计算在原图像(利用积分图)。而SIFT是计算在高斯金字塔上(注意不是高斯差分金字塔。)
性能的比较:
论文:A comparison of SIFT, PCA-SIFT and SURF 对三种方法给出了性能上的比较,源图片来源于Graffiti dataset,对原图像进行尺度、旋转、模糊、亮度变化、仿射变换等变化后,再与原图像进行匹配,统计匹配的效果。效果以可重复出现性为评价指标。
比较的结果如下:
| method |
Time |
Scale |
Rotation |
Blur |
Illumination |
Affine |
| Sift |
common |
best |
best |
common |
common |
good |
| Pca-sift |
good |
good |
good |
best |
good |
best |
| Surf |
best |
common |
common |
good |
best |
good |
由此可见,SIFT在尺度和旋转变换的情况下效果最好,SURF在亮度变化下匹配效果最好,在模糊方面优于SIFT,而尺度和旋转的变化不及SIFT,旋转不变上比SIFT差很多。速度上看,SURF是SIFT速度的3倍。
Ⅳ、主成成分分析pca算法 原理解析
目前,pca算法已经广泛应用于各方面,就拿图像处理,经常做的一件事就是当提取的图像特征维度比较高时,为了简化计算量以及储存空间,需要对这些高维数据进行一定程度上的降维,并尽量保证数据的不失真。
先举个例子,方便理解:
1)对于一个训练集,100个sample(i=1,2,3,...,100),特征Xi是20维.[Xi1,Xi2,Xi3,...Xij,...,Xi20](j=1,2,..,20),那么它可以建立一个20*100的样本矩阵M。
2)紧接着我们开始求这个样本的协方差矩阵,得到一个20*20的协方差矩阵,计算过程如下:
•先求解出Xi的平均Xav=(∑xi)/20;
•对每一个Xi,计算Xi-Xav,即Mi(第 i 行)变为 Mi-Xav,记为Mn;
•则容易得到协方差矩阵Z为Mn*Mn'( ' 表示转置 ) 。
3)然后求出这个协方差矩阵Z20x20的特征值和特征向量,一般情况下应该有20个特征值和特征向量,现在根据特征值的大小,取出较大的特征值以及其所对应的特征向量,(假设提取的特征值为较大的5个特征值),那么这5个特征向量就会构成一个20*5的矩阵V,这个矩阵就是我们要求的特征矩阵。
4)用Mn'去乘以V,得到一个base矩阵(*),大小为100x5。
5)任取一个样本1x100,乘上这个100*5的特征矩阵,就得到了一个1*5的新的样本,显然每个sample的维数下降了,然后再用这个1x5向量去比较相似性。
注:
›上述3)过程中特征值的选取在不确定具体要降到多少维的情况下,一般还可以根据n个特征值之和大于总和的90%进行选取。
›上面的(*)处base矩阵的求解不唯一,也可以自行修正。
大致说完了PCA降维的过程,现在会有人要问为什么只提取特征值较大的几个特征值就可以近似代替原样本矩阵呢。
好了,话不多说。下面就讲讲矩阵的特征值和特征向量的数学意义:
为简单起见,以二维矩阵A=[1 0;0 -1](矩阵的秩为2)为例,以平面上一点(x,y)经过A变换后变为(x',y')若这两点在一条直线在,那么可以理解为矩阵A的作用恰好使得向量[x y]' 只是在原有方向上变换了长度而已,即Ax=λx (x为一列向量).对于A矩阵,容易得到A的两个特征值及相应的特征向量 λ1=1 ,e1=[1 0]' , λ2=-1 ,e2=[0 -1]' ,二维平面上任意一点(x,y)=b1*(1,0)+b2*(0,-1)(b1,b2均为实常数); 那么A[x y]'=A*(b1*e1+b2*e2)=b1*λ1+b2*λ2 =∑biλi ;
把这个公式推广到高维空间,在计算(x',y')对于λ值比较小的特征维可以忽略.
B=[1 0;0 0.01] ,其中B的两个特征值及相应的特征向量 λ1=1 ,e1=[1 0]' , λ2=0.01 ,e2=[0 1]'
那么x=[2 3]' 经过B变换为 Bx=[2 0.03]';
如果我们认为λ2远小于λ1,忽略掉λ2时,Bn=[1 0;0 0],Bnx=[2 0]'≈[2 0.03].
通俗点讲,pca算法就是去寻找那些在该维度上方差比较大的维,同时忽略比较平均的维度。假如上面所说的X特征向量的第一个元素都为1,那么这一列数据是可以忽略的,因为他并不能起到区分的作用,相反我们是要寻找那些在某一维度分布比较广的维,并提取出来。
打个比方,平面区域一个斜75度的椭圆,且长轴远大于短轴,那么椭圆上的点在短轴上的分布明显弱于长轴,当短轴远小于长轴时,近似为一条直线,便失去了短轴这个维度。