直方图均衡化算法实现
直方图
直方图(histogram)是灰度级的函数,它表示图像中具有每种灰度级的像素的个数,
反映原图中各种灰度值分布的情况。
如下图所示,灰度直方图的横坐标是灰度级,纵坐标是该灰度级出现的频率,是图像的最基本的统计特征。
上面的是标准直方图
灰度统计累计直方图:
H(k)= ∑ni(i<=k)
累积直方图中第k列的高度是图像中所有灰度值<=k的像素的个数
灰度直方图的求取算法实现
void GetHistogram(BYTE *image_Src, int width, int height, unsigned long *histogram)
{
int pixelCount = width*height;//imageSize->pixelCount
memset(histogram, 0, 256*4);//注意最后一个参数是数组的大小(单位是字节)
for (int i = 0; i <= pixelCount - 1; ++i)
{
int gray = image_Src[0];
histogram[gray]++;
//下一个像素
image_Src+=1;
}
}
直方图的特点
直方图具有很多的优点,直方图能反映图像的概貌,
-
图像中有几类目标,目标和背景的分布如何;
-
通过直方图可以直接计算图像中的最大亮度、最小亮度、平均亮度、对比度以及中间亮度等。
-
使用直方图可以完成图像分割、目标检索等。因为不同的目标具有不同的颜色分布。使用归一化直方图作目标匹配,还不易受到目标翻转和目标大小变化的影响。
-
在图像查询的系统中,直方图有很大的应用,用它存储目标的特征占有空间小,且执行速度快。
-
其缺点:因其没有记录位置信息,不同的图像会具有相同或相近的直方图。一幅图像旋转、翻转后的直方图是相同的;放大、缩小后的直方是相近的。
直方图均衡化
原理
为了增强图像整体的对比效果,增加灰度值的动态范围
由图像点运算可知,图像增强的公式可以表示为
G(x,y)=F(g(x,y))
这里,由于要增强对比效果,所以
这里假设原图灰度级范围位为采用归一化的[0,1]
-
F()在整个灰度级范围[0,1]内是递增函数(因为要增强对比)
-
F()的值域也是[0,1]
可以证明累计分布函数满足上面的变换函数要求,而图像中,这个累计分布函数,就是原始图像的累计直方图。
F()通常都是作为查找表LUT出现的,因为是离散的,所以累计直方图也是可以作为LUT出现
实际上:累计分布直方图作为图像变换函数(本质为LUT)。从而将增强了原图像的对比效果。而通常图像变换函数是离散的,通过LUT实现,所以通过累计分布直方图作就可以实现直方图均衡化。
也可以用熵的原理来解释均衡化原理:
熵(Entropy):是信息量的度量,其定义为:
其中, pi是符号 i出现的概率。 在图像中,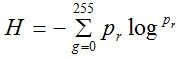 pr是灰度级r 出现的概率。
pr是灰度级r 出现的概率。
可以证明,当p0=p1=p2=…=p255=1/256时,H取最大值,即图像信息量最大。
根据熵理论可知,直方图中,当H[0],H[1]…,H[n-1]相等时,图像信息量最大-》均衡化的目的是使每个Hi都相等,即把原始图的直方图变换为均匀分布的形式,这样就增加了象素值的范围,增强了图像的对比效果。
对于熵这个概念,我也是费了好大的劲才大概能够明白他的意思:
熵越大,系统的不确定性越大,系统越混乱,从而信息量也就越大。
对于单个信息,可以理解为发生的概率越小 ,熵越大
对于一个系统,如果系统由多个部分组成,则可以理解为各个部分发生概率基本相等时熵最大
关于熵的概念,大家可以参考吴军老师的《数学之美》中关于熵的解释,比较通俗易懂。
直方图均衡化算法实现
void GetHistogramEqualize(BYTE *image_Src,BYTE *image_Dst, int width, int height)
{
//-------step 1.求灰度直方图
unsigned long historgam[256];
GetHistogram(image_Src, width, height, historgam);
//------step 2.求累计分布直方图(灰度变换函数,LUT)
//累计分布直方图符合增强对比度函数的要求
int LUT[256];
LUT[0] = historgam[0];
int sum = historgam[0];
for (int i = 1; i <= 255; ++i)
{
sum += historgam[i];
LUT[i] =255* sum / (width*height);
}
//----step 3.对原图像做图像增强
int pixelCount = width*height;
for (int i = 0; i <= pixelCount - 1; ++i)
{
int gray = image_Src[i];
image_Dst[i] = LUT[gray];
}
}
效果图(借助了Opencv来显示图片)