【强连通分量】耍朋友

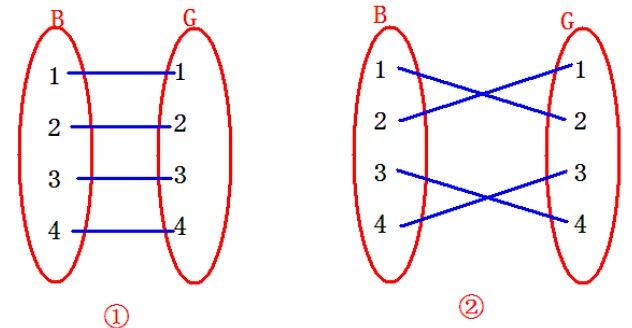
【问题描述】
春天来了，乐乐在某一天的中午做了一个奇怪而又温馨的梦，以下是梦境的描述：
绵中21XX 级信奥班实现了男女人数平均，欧教本着“人人都有朋友耍，人人都有一等
拿”的教学原则，准备为机房的每个同学牵红线。并且由于21XX 年世界男女比例对男生有
利，所以只要一个男生喜欢一个女生，他们就可以耍朋友（耶~！）。
现给出每个男生喜欢哪些女生（没错，是哪些，因为在乐乐的梦里一个男生喜欢N 个
女生都是很符合逻辑的），并给出欧教已经安排好的一种匹配方式。
问：在满足“人人都有朋友耍”的原则下，每个男生可以和哪些女生耍朋友而不会出现
让其他男生无朋友可耍的情况（包括欧教已经安排好的原配）。
【输入数据】
第一行一个整数n，表示有n 个男生和n 个女生。
接下来n 行每行若干个整数m，a1，a2，…，am。第i 行表示第i 个男生喜欢m 个女生，她
们分别是a1，a2，…，am。
最后一行共n 个整数，第i 个整数di 表示欧教给出的第i 个男生的原配是di。
【输出数据】
共 n 行，每行若干个整数c，b1，b2，…，bc。第i 行表示第i 个男生可以和c 个女生耍朋
友，这些女生是b1，b2，…，bc。（女生的编号务必按照从小到大的顺序输出，女孩包含欧
教事先给出的原配。）
【样例输入】
4
2 1 2
2 1 2
2 3 4
2 3 4
1 2 3 4
【样例输出】
2 1 2
2 1 2
2 3 4
2 3 4
【样例解释】
图①为一种匹配方式（欧教给出的原配）；图②为满足原则的另一种匹配。

【数据范围及约定】
1≤n≤2000。
由于大家都还是高中生，不会特别花心，所以总的关系数不会超过150000 条。

这道题一看到很像二分图匹配。
但是看到题目，总是会感觉匈牙利算法怎么用都用不上。
于是，我们沿着匈牙利算法的思路来继续想这道题。
首先，匈牙利算法从左半集出发，通过一条匹配边、一条非匹配边、一条匹配边……最终到达右半集，这时匹配数+1。
能不能用类似这样的方法但让匹配数不加一呢？（也就是换一个匹配。）
当然可以！直接构成一个环就行了。

于是，将所有原配建成从右到左的边，把其余的建成从左到右的边，这样就可以用Tarjan找出强连通分量，最后在所有的强连通分量中找出其中含有的边即可，即为所有可行的匹配。
Accode：

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <string>
#define min(a, b) ((a) < (b) ? (a) : (b))

const int maxN = 2010;
struct Edge {int v; Edge *next;};
Edge *edge[maxN << 1];
bool marked[maxN << 1], mp[maxN][maxN];
int DFN[maxN << 1], Low[maxN << 1];
int stack[maxN << 1], Belong[maxN << 1];
int Link[maxN], n, Bcnt, Ind, top;

inline int getint()
{
    int res = 0; char tmp;
    while (!isdigit(tmp = getchar()));
    do res = (res << 3) + (res << 1) + tmp - '0';
    while (isdigit(tmp = getchar()));
    return res;
}

inline void Ins(int u, int v)
{
    Edge *p = new Edge; p -> v = v;
    p -> next = edge[u]; edge[u] = p;
    return;
}

void Tarjan(int u)
{
    DFN[u] = Low[u] = ++Ind;
    marked[stack[++top] = u] = 1;
    for (Edge *p = edge[u]; p; p = p -> next)
    {
        if (!DFN[p -> v])
        {
            Tarjan(p -> v);
            Low[u] = min(Low[u], Low[p -> v]);
        }
        else if (marked[p -> v])
            Low[u] = min(Low[u], DFN[p -> v]);
    }
    if (DFN[u] == Low[u])
    {
        int tmp = u; ++Bcnt;
        do
        {
            tmp = stack[top--];
            marked[tmp] = 0;
            Belong[tmp] = Bcnt;
        }
        while (tmp != u);
    }
    return;
}

int main()
{
    freopen("love.in", "r", stdin);
    freopen("love.out", "w", stdout);
    n = getint();
    for (int i = 1; i < n + 1; ++i)
    for (int cnt = getint(); cnt; --cnt)
        mp[i][getint()] = 1;
    for (int i = 1; i < n + 1; ++i)
    {
        int j = getint();
        Link[j] = i;
        Ins(j + n, i);
    }
    for (int i = 1; i < n + 1; ++i)
    for (int j = 1; j < n + 1; ++j)
    if (mp[i][j] && Link[j] != i)
        Ins(i, j + n);
    for (int i = 1; i < n + 1; ++i)
        if (DFN[i]) Tarjan(i);
    for (int i = 1; i < n + 1; ++i)
    {
        int cnt = 0;
        for (int j = 1; j < n + 1; ++j)
        if (mp[i][j] && Belong[i] == Belong[j + n])
            ++cnt;
        printf("%d", cnt);
        for (int j = 1; j < n + 1; ++j)
        if (mp[i][j] && Belong[i] == Belong[j + n]) //
            printf(" %d", j);
        printf("\n");
    }
    return 0;
}

#undef min