【半枚举】【动态规划】【NOI2004】曼哈顿

【问题描述】
P城是M国的著名旅游城市。在市长G先生的治理下，人民安居乐业，城市欣欣向荣。然而，G市长并没有被自己的政绩冲昏头脑，他清醒地意识到城市的治理还存在着一些问题，其中之一就是交通问题。
P城有m条横向街道和n条纵向街道，横向街道横贯东西，纵向街道纵穿南北，构成了P城整齐的交通网络（如图1所示）。

由于街道狭窄，每条街道都只允许单向行驶，单向行驶的方向是事先设定好了的。一条横向街道的行驶方向只能是向东或者向西，一条纵向街道的行驶方向只能是向南或者向北，逆向行驶是绝对禁止的。
这项限制给交通带来了巨大的不便。如图1，很多游人希望从宾馆前往购物中心，但限于街道的行驶方向，他们不得不绕一个大圈才能够到达。
这个问题一直困扰着G市长，每天他都会收到不少游人的来信，抱怨P城不合理的交通设计。但由于街道数目过多，他和他的部下始终不能解决这个问题……
令人高兴的是这个问题不久就可能得以解决。因为最近他们以重金聘请了著名的交通规划大师B先生，请他对P城的交通进行有效合理的改造。
B先生知道不能通过拓宽街道的方法解决问题，因为这样势必影响到街道两旁的旅游景点，这是大家都不希望看到的。于是他准备重新设计街道的行驶方向（整条街道的行驶方向），使之尽可能满足大家的要求。
B先生先把P城的街道编号，横向街道由北向南编号为1，2，……，m，纵向街道由西向东编号为1，2，……，n。这样任何一个十字路口的位置都可以用一对正整数来表示，第一个数是该路口所在的横向街道的编号，第二个数是它所在的纵向街道的编号，这对整数被称为该十字路口的坐标。比如图1中宾馆所在的十字路口的坐标是(2,3)。
经过长期调查，他整理出了游人们提得相对集中的一些要求。每条要求都可以写成如下的形式：从一个十字路口到另一个十字路口的最短路径的长度必须等于它们之间的曼哈顿距离。所谓曼哈顿距离是指两个十字路口在东西方向上的距离加上在南北方向上的距离，坐标分别为(x1,y1)和(x2,y2)的两个十字路口之间的曼哈顿距离为|x1-x2|+|y1-y2|。
好了，B先生已经知道了P城目前所有街道的行驶方向和游人们提得相对集中的要求，他能不能重新设计街道的行驶方向，使之满足所有要求呢？
另外，改变每条街道的行驶方向都有一定的工作量，工作量的大小因道路而异。B先生不仅想找到一个可行的改造计划，而且还希望这个计划的总工作量尽可能小。你能帮帮他吗？

【输入文件】
输入文件的第一行有两个正整数m和n，分别表示横向街道和纵向街道的数目。
第二行是一个长度为m的字符串，由北向南列出了m条横向街道改造前的行驶方向。E表示向东，W表示向西。
第三行是一个长度为n的字符串，由西向东列出了n条纵向街道改造前的行驶方向。S表示向南，N表示向北。
第四行有m个非负整数，由北向南列出了改变每条横向街道的行驶方向的工作量。
第五行有n个非负整数，由西向东列出了改变每条纵向街道的行驶方向的工作量。
第六行是一个正整数k，表示游人们提得相对集中的要求的数目。
接下来的k行，每行有四个正整数x1，y1，x2，y2，表示一条要求。这条要求的内容是希望从坐标为(x1,y1)的十字路口到坐标为(x2,y2)的十字路口的最短路径的长度等于这两个路口之间的曼哈顿距离。

【输出文件】
第一行是一个字符串，“possible”或者“impossible”（引号不输出）。输出“possible”表示可以通过改变街道的行驶方向满足输入数据中的所有要求，输出“impossible”表示无论怎么设计都不可能满足输入数据中的所有要求。
如果在第一行输出的是“possible”的话，在第二行输出一个整数，表示最小的总工作量，在第三行输出一个长度为m的字符串，由北向南列出改造后的m条横向街道的行驶方向，E表示向东，W表示向西，在第四行输出一个长度为n的字符串，由西向东列出改造后的n条纵向街道的行驶方向， S表示向南，N表示向北。

【约定】

改变一条街道的行驶方向的工作量不超过10000

【样例输入】
2 3
WE
NNS
3 9
1 4 2
2
1 3 2 1
2 3 2 2

【样例输出】
possible
9
WW
NNS

【评分方法】
如果你的输出文件的第一行是“impossible”，
如果确实无解，则该测试点满分。
如果实际有解，则该测试点0分。
如果你的输出文件的第一行是“possible”，
如果你的程序输出的方案不可行，则该测试点0分。
如果你的程序输出的总工作量与实际总工作量不一致，则该测试点0分。
如果你的程序输出的方案可行，但总工作量不是最小的，则该测试点4分。
如果你的程序输出的方案可行，且总工作量最小，则该测试点满分。

刚开始拿到此题时完全无思路，只是看着m很小，以为是状压……
看了题解之后，发现此题不过如此。

首先m很小，可以直接枚举，然后直接在n上进行动态规划。

可以发现使满足一个要求的方法有四种（设要求的起点为(x0, y0)，终点为(x1, y1)）。

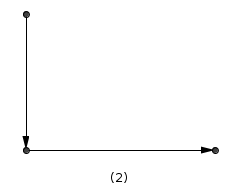
 (1) 在x0横道方向符合，而x1横道方向不符合要求，那么y1纵道的方向必须符合要求；
 (2) 在x0横道方向不符合，而x1横道方向符合要求，那么y0纵道的方向必须符号要求；
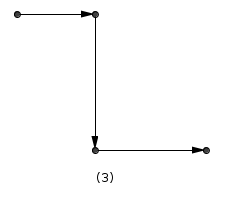
 (3) 在x0、x1横道方向都符合，那么y0到y1之间必须至少有一个纵道的方向符合要求；
 (4) 在x0、x1横道方向都不符合，那么x0到x1之间必须至少有一个横道的方向符合要求，并且y0、y1纵道的方向都必须符合要求。

于是，在半枚举横向道路的基础上，每个要求都可以转化以下问题：
在编号在一个区间的纵向街道至少一条街道的方向与该要求的方向一致。
不妨记向下为1，向上为0；向右为1，向左为0。
若区间存在包含关系，则可以将较大的区间去掉。
将所有的区间从左到右排序（方向为0的区间和方向为1的区间分开考虑），那么可以用动态规划的方法解决此问题。

令f[i][j0][j1]表示确定了[0, i)的纵向街道的方向，满足了编号为[0, j0)的0区间和编号为[0, j1)的1区间的要求所需的最小代价（不包含横向街道，其代价在半枚举的时候算出）。
那么：
若第i条街道的方向为0，则从f[i][j0][j1]可以推出状态f[i + 1][j0`][j1]，代价为把第i条纵向街道变为0的代价，j0`为第一个左边界大于i的0区间的编号；
若第i条街道的方向为1，则从f[i][j0][j1]可以推出状态f[i + 1][j0][j1`]，代价为把第i条纵向街道变为1的代价，j1`为第一个左边界大于i的1区间的编号；

注意每个j0(j1)的枚举下界：第一个右边界大于等于i的0(1)的区间的编号；上界：j0`(j1`)。

还要注意当一个要求的起点与终点重合时，应将其忽略掉。
代码：

/*****************************\
 * @prob: NOI2004 manhattan  *
 * @auth: Wang Junji         *
 * @stat: Accepted.          *
 * @date: June. 9th, 2012    *
 * @memo: 半枚举、动态规划     *
\*****************************/
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <string>

const int maxN = 110, maxM = 20, maxK = 110, INF = 0x3f3f3f3f;

struct Req {int x0, x1, y0, y1;} req[maxK];
struct Seg
{
    int L, R; Seg() {}
    Seg(int _L, int _R): L(std::min(_L, _R)), R(std::max(_L, _R)) {}
    bool operator<(const Seg& b) const {return L < b.L || (L == b.L && R < b.R);}
} seg[2][maxN << 1]; char sx[maxN], sy[maxN];
struct Record
{
    int j0, j1, dir; Record() {}
    Record(int j0, int j1, int dir): j0(j0), j1(j1), dir(dir) {}
};
int dir_x, dir_y[maxN], _dir_x[maxM], _dir_y[maxN];
int cost_x[maxM], cost_y[maxN], upr[2][maxN], lwr[2][maxN], cnt[2];
int n, m, K, ans = INF;

inline void simplify(Seg* seg, int& cnt)
{
    static bool exclusive[maxN << 1];
    memset(exclusive, 0, sizeof exclusive);
    for (int i = 0; i < cnt - 1; ++i) if (!exclusive[i])
    for (int j = i + 1; j < cnt; ++j) if (seg[i].L >= seg[j].L)
        exclusive[j] = 1;
    int new_cnt = 0;
    for (int i = 0; i < cnt; ++i)
        if (!exclusive[i]) seg[new_cnt++] = seg[i];
    cnt = new_cnt; return;
}

inline bool cmp(const Seg& a, const Seg& b)
{return a.R < b.R || (a.R == b.R && a.L > b.L);}

inline void get_upr(Seg* seg, int& cnt, int* upr)
{
    for (int i = 0; i < n; ++i)
        upr[i] = std::upper_bound(seg, seg + cnt, Seg(i, INF)) - seg;
    return;
}

inline void get_lwr(Seg* seg, int& cnt, int* lwr)
{
    for (int i = 0; i < n; ++i)
        lwr[i] = std::lower_bound(seg, seg + cnt, Seg(i, i), cmp) - seg;
    return;
}

inline bool prepare()
{
    cnt[0] = cnt[1] = 0;
    for (int i = 0; i < K; ++i)
    {
        bool cur_dir_x = req[i].y0 < req[i].y1, cur_dir_y = req[i].x0 < req[i].x1,
             dir_x_x0 = (dir_x >> req[i].x0) & 1, dir_x_x1 = (dir_x >> req[i].x1) & 1;
        if (req[i].x0 == req[i].x1)
        {
            if (req[i].y0 != req[i].y1 && dir_x_x0 != cur_dir_x) return 0;
            else continue;
        }
        if (req[i].y0 == req[i].y1)
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y0, req[i].y1);
        else if (!(dir_x_x0 ^ cur_dir_x) && !(dir_x_x1 ^ cur_dir_x))
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y0, req[i].y1);
        else if ((dir_x_x0 ^ cur_dir_x) && !(dir_x_x1 ^ cur_dir_x))
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y0, req[i].y0);
        else if (!(dir_x_x0 ^ cur_dir_x) && (dir_x_x1 ^ cur_dir_x))
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y1, req[i].y1);
        else
        {
            bool flag = 0;
            for (int j = req[i].x0; j != req[i].x1; cur_dir_y ? ++j : --j)
                if (!(((dir_x >> j) & 1) ^ cur_dir_x)) {flag = 1; break;}
            if (!flag) return 0;
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y0, req[i].y0);
            seg[cur_dir_y][cnt[cur_dir_y]++] = Seg(req[i].y1, req[i].y1);
        }
    }
    std::sort(seg[0], seg[0] + cnt[0], cmp); simplify(seg[0], cnt[0]);
    std::sort(seg[1], seg[1] + cnt[1], cmp); simplify(seg[1], cnt[1]);
    get_upr(seg[0], cnt[0], upr[0]); get_upr(seg[1], cnt[1], upr[1]);
    get_lwr(seg[0], cnt[0], lwr[0]); get_lwr(seg[1], cnt[1], lwr[1]);
    seg[0][cnt[0]] = seg[1][cnt[1]] = Seg(INF, INF); return 1;
}

int Dp()
{
    static int f[maxN][maxN][maxN];
    static Record g[maxN][maxN][maxN];
    memset(f, 0x3f, sizeof f); f[0][0][0] = 0;
    for (int i = 0; i < n; ++i)
    for (int j0 = lwr[0][i]; j0 < upr[0][i] + 1; ++j0)
    for (int j1 = lwr[1][i]; j1 < upr[1][i] + 1; ++j1)
    if (f[i][j0][j1] < INF)
    {
        if (f[i][j0][j1] + cost_y[i] * _dir_y[i] < f[i + 1][upr[0][i]][j1])
            f[i + 1][upr[0][i]][j1] = f[i][j0][j1] + cost_y[i] * _dir_y[i],
            g[i + 1][upr[0][i]][j1] = Record(j0, j1, 0);
        if (f[i][j0][j1] + cost_y[i] * !_dir_y[i] < f[i + 1][j0][upr[1][i]])
            f[i + 1][j0][upr[1][i]] = f[i][j0][j1] + cost_y[i] * !_dir_y[i],
            g[i + 1][j0][upr[1][i]] = Record(j0, j1, 1);
    }
    int i = n, j0, j1, j0_nxt = cnt[0], j1_nxt = cnt[1];
    while (i--)
    {
        j0 = g[i + 1][j0_nxt][j1_nxt].j0, j1 = g[i + 1][j0_nxt][j1_nxt].j1;
        dir_y[i] = g[i + 1][j0_nxt][j1_nxt].dir;
        j0_nxt = j0, j1_nxt = j1;
    }
    return f[n][cnt[0]][cnt[1]];
}

int main()
{
    freopen("manhattan.in", "r", stdin);
    freopen("manhattan.out", "w", stdout);
    scanf("%d%d%s%s", &m, &n, sx, sy);
    for (int i = 0; i < m; ++i) _dir_x[i] = sx[i] == 'E';
    for (int i = 0; i < n; ++i) _dir_y[i] = sy[i] == 'S';
    for (int i = 0; i < m; ++i) scanf("%d", cost_x + i);
    for (int i = 0; i < n; ++i) scanf("%d", cost_y + i);
    scanf("%d", &K);
    for (int i = 0; i < K; ++i)
        scanf("%d%d%d%d", &req[i].x0, &req[i].y0, &req[i].x1, &req[i].y1),
        --req[i].x0, --req[i].y0, --req[i].x1, --req[i].y1;
    for (dir_x = 0; dir_x < 1 << m; ++dir_x)
    {
        if (!prepare()) continue; int Now = 0;
        for (int i = 0; i < m; ++i)
            Now += (((dir_x >> i) & 1) ^ _dir_x[i]) * cost_x[i];
        if ((Now += Dp()) < ans)
        {
            ans = Now;
            for (int i = 0; i < m; ++i) sx[i] = ((dir_x >> i) & 1) ? 'E' : 'W';
            for (int i = 0; i < n; ++i) sy[i] = dir_y[i] ? 'S' : 'N';
        }
    }
    if (ans == INF) printf("impossible\n");
    else printf("possible\n%d\n%s\n%s\n", ans, sx, sy);
    return 0;
}