杭电OJ——1016 Prime Ring Problem

Prime Ring Problem

Problem Description

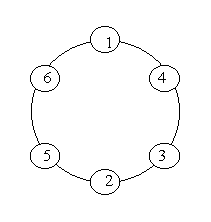
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.

Note: the number of first circle should always be 1.

 

Input

n (0 < n < 20).

 

Output

The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.

You are to write a program that completes above process.

Print a blank line after each case.

 

Sample Input

     
     
     
     

      
      
      
      6
8
     
     
     
     

 

Sample Output

     
     
     
     

      
      
      
      Case 1:
1 4 3 2 5 6
1 6 5 2 3 4

Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
     
     
     
     

 

Source

Asia 1996, Shanghai (Mainland China)

 

 

在博客园里看到一篇很好的讲解素数环的文章，因此copy过来分享分享，今天看了这篇文章，懂了很多，原来代码还可以这么优化！认真看，绝对物有所值！

素数环-谈代码优化

昨天在博问里面看到的一道算法题，原题如下：

给出一个N(0<N<20)，在1~N的所有排列中，满足相邻两个数之和是素数（头尾相邻）的排列输出

比如当N = 4时，满足条件的素数环有如下几种

1 2 3 4
1 4 3 2
2 1 4 3
2 3 4 1
3 2 1 4
3 4 1 2
4 1 2 3
4 3 2 1

常规的做法是，找出这N个数的所有排列，然后依次检查每个排列，筛选出符合条件的排列即可。求排列可以用回溯法的排列树模型，筛选就按照题目要求即可，判断素数的算法也有很多，选择一个即可。注意不要忘记最后一个元素和第一个元素的检测。优化前的代码如下:

代码

 1  //  Is n prime ?
 2  bool  IsPrime( int  n)
 3  {
 4       for  ( int  i  =   2 ; i  *  i  <=  n; i ++ )
 5           if (n  %  i  ==   0 )
 6               return   false  ;
 7       return   true  ;
 8  }
 9 
10  //  Check a permutation
11  bool  Check( int  a[],  int  n)
12  {
13       if ( ! IsPrime(a[ 0 ]  +  a[n  -   1 ]))
14           return   false  ;
15 
16       for ( int  i  =   0 ; i  <  n  -   1 ; i ++ )  //  avoid duplicate
17           if ( ! IsPrime(a[i]  +  a[i  +   1 ]))
18               return   false  ;
19 
20       return   true  ;
21  }
22 
23  void  Perm( int  a[],  int  n,  int  t)
24  {
25       if (t  ==  n)
26      {
27           if (Check(a, n))
28              Output(a, n) ;
29      }
30       else
31      {
32           for ( int  k  =  t; k  <  n; k ++ )
33          {
34              swap(a[k], a[t]) ;
35              Perm(a, n, t  +   1 ) ;
36              swap(a[k], a[t]) ;
37          }
38      }
39  }

题目不难，做完以后，我发现有很多可以优化的地方，可以大幅提高速度。

1. 首先，找出所有排列并逐个检查，这是很浪费时间的，更高效的方法是，一边排列一边检查，这样可以提早发现不满足条件的候选解，提早剪枝，避免不必要的搜索，例如当N=10时，排列到1234的时候，满足条件，下一次选择5，序列变为12345，由于4 + 5 = 9，非素数，所以后面不用再排列了，也就是从当前位置开始，以5为根的子树可以不用再搜索了，直接跳到6，序列变为12346，由于4 + 6 = 10，非素数，同样舍弃6为根的子树。下一次搜索变成12347，这回满足条件，继续排列下一个元素，如此直到10个元素全部排列完成。代码如下：a是储存排列的数组，n是元素个数，t用来控制递归过程。

 1  void  PrimeCircle( int  a[],  int  n,  int  t)
 2  {
 3       if (t  ==  n)
 4      {
 5          Output(a, n) ;  //  找到一个解
 6      }
 7       else
 8      {
 9           for ( int  i  =   1 ; i  <=  n; i ++ )
10          {
11              a[t]  =  i ;
12               if (IsOk(a))  //  检查当前值，满足条件才继续
13                  PrimeCircle(a, n, t  +   1 ) ;
14          }
15      }
16  }

2. 再看题目的输入范围，1 < N < 20，由于输入规模比较小，所以考虑使用查表法来判定素数，查表法是典型的以空间换时间的方法。20以内两个数之和最大是18 + 19 = 37，而37以内的素数分别是2， 3， 5， 7， 11， 13， 17， 19， 23， 29， 31， 37，我们可以定义一个38个元素的数组，当i为素数时，令a[i] = 1，否则a[i] = 0。这样，要判断一个数是否为素数时，直接判断a[i]是否为1即可。对应的数组如下：

 1  int  prime[ 38 ]  =  
 2  {
 3       0 ,  0 ,  1 ,  1 ,  0 ,  1 ,  0 , 
 4       1 ,  0 ,  0 ,  0 ,  1 ,  0 ,  1 , 
 5       0 ,  0 ,  0 ,  1 ,  0 ,  1 ,  0 , 
 6       0 ,  0 ,  1 ,  0 ,  0 ,  0 ,  0 , 
 7       0 ,  1 ,  0 ,  1 ,  0 ,  0 ,  0 ,
 8       0 ,  0 ,  1 ,
 9  } ;

判断i是否为素数的代码也很简单

1  if  (prime[i]  ==   1 )   // 素数
2  {
3       //  do something
4  }

3. 再考虑输入的特点，如果输入N是奇数的话，由于起点从1开始，那么1-N之间一共有N / 2个偶数，N / 2 + 1个奇数，也就是奇数的个数比偶数多一个，那么把这N个数排成一个环，根据鸽巢原理，必然有两个奇数是相邻的，而两个奇数之和是偶数，偶数不是素数，所以我们得出结论，如果输入N是奇数的话，没有满足条件的排列。这样当N是奇数的时候，直接返回即可。如果1-N之间每个数输入的几率相同，这个判断可以减少一半的计算量。

1  if (n  &   1 )  //  奇数无解，直接返回
2       return  ;
3 

4. 扩展一下第三点，可以发现，任何一个满足条件的排列都有一个共同点：相邻的两个数奇偶性必然不同，原因是：两个奇数之和或者两个偶数之和都是偶数，而偶数一定不是素数，所以在选取当前元素的时候，比较一下它和前一个元素的奇偶性。再做决定，可以减少一部分计算量。

由 于奇数 + 偶数 = 奇数, 而奇数的二进制表示中,最低位是1, 所以有下面的代码, 其中curValue是当前值, a[lastIndex]是前一个值.

1  if ( ! ((curValue  +  a[lastIndex])  &   1 ))  //  相邻的数奇偶性必然不同
2       return   false  ;
3 

经过上面的优化，代码如下，应该会比原来快很多。还有什么地方可以优化么？欢迎讨论！

代码

 1  #include  < iostream >
 2  using   namespace  std ;
 3 
 4  //  小于37的所有素数
 5  int  prime[ 38 ]  =  
 6  {
 7       0 ,  0 ,  1 ,  1 ,  0 ,  1 ,  0 , 
 8       1 ,  0 ,  0 ,  0 ,  1 ,  0 ,  1 , 
 9       0 ,  0 ,  0 ,  1 ,  0 ,  1 ,  0 , 
10       0 ,  0 ,  1 ,  0 ,  0 ,  0 ,  0 , 
11       0 ,  1 ,  0 ,  1 ,  0 ,  0 ,  0 ,
12       0 ,  0 ,  1 ,
13  } ;
14 
15  //  输出一个解
16  void  Output( int  a[],  int  n)
17  {
18       for ( int  i  =   0 ; i  <  n; i ++ )
19          cout  <<  a[i]  <<   "   "  ;
20      cout  <<  endl ;
21  }
22 
23  //  判断当前序列是否满足条件
24  bool  IsOk( int  a[],  int  lastIndex,  int  curValue)
25  {
26       if (lastIndex  <   0 )  //  第一个元素没有前驱元素，返回真
27           return   true  ;
28 
29       if ( ! ((curValue  +  a[lastIndex])  &   1 ))  //  相邻的数奇偶性必然不同
30           return   false  ;
31 
32       if ( ! prime[a[lastIndex]  +  curValue])  // 相邻元素和为素数
33           return   false  ;
34 
35       for ( int  i  =   0 ; i  <=  lastIndex; i ++ )  //  去重，curValue没有出现过
36           if (a[i]  ==  curValue)
37               return   false  ;
38 
39       return   true  ;
40  }
41 
42  void  PrimeCircle( int  a[],  int  n,  int  t)
43  {
44       if (n  &   1 )  //  奇数无解，直接返回
45           return  ;
46 
47       if (t  ==  n) 
48      {
49           if (prime[a[ 0 ]  +  a[n  -   1 ]]);  //  判断首尾元素
50              Output(a, n) ; 
51      }
52       else
53      {
54           for ( int  i  =   1 ; i  <=  n; i ++ )
55          {
56              a[t]  =  i ;
57               if (IsOk(a, t  -   1 , i))  // 如果当前元素满足条件
58                  PrimeCircle(a, n, t  +   1 ) ;  // 进行下一次递归
59          }
60      }
61  }
62 
63  int  main( void )
64  {
65       int  a[ 20 ] ;
66       const   int  n  =   4  ;  //  4个元素的排列
67      PrimeCircle(a, n,  0 ) ;
68      
69      system( " pause " ) ;
70       return   0  ;
71  }

发一下AC代码：

//Prime Ring Problem
//这个程序也可以实现，得出正确答案，不过超时！
/*
#include <cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const SIZE=20;

int ring[38] = 
 {
     0, 0, 1, 1, 0, 1, 0, 
     1, 0, 0, 0, 1, 0, 1, 
     0, 0, 0, 1, 0, 1, 0, 
     0, 0, 1, 0, 0, 0, 0, 
     0, 1, 0, 1, 0, 0, 0,
     0, 0, 1,
 } ;
int k=1;
int Judge(int a[],int num)
{
	   int n; 
	   n=a[0]+a[num-1];
	   if(!ring[n]) return 0;
	   for(int k=0;k<num-1;k++)
		{   
			  n=a[k]+a[k+1];
			if(!ring[n]) return 0;
	   }
		return 1;//运行到这一步，表明是素数环
}

int main()
{
	int num=6,i;
	int prime[SIZE];
	while(1)
	{
		scanf("%d",&num);
		for(i=0;i<num;i++)
			prime[i]=i+1;
		printf("Case %d:\n",k);
		k++;
		do
		{
			if(Judge(prime,num))
			{
				
				
				for(i=0;i<num;i++)
				printf("%d ",prime[i]);
                printf("\n");
			}
		}while (next_permutation(prime+1,prime+num));//主要调用next_permutation函数
		printf("\n");
	}
	
	return 0;
}
*/

//这个算法很巧妙，真正佩服想出来的人！
#include <iostream>
#include<cstdio>
using namespace std;
 
// 小于37的所有素数
 int prime[38]= 
 {
     0, 0, 1, 1, 0, 1, 0, 
     1, 0, 0, 0, 1, 0, 1, 
     0, 0, 0, 1, 0, 1, 0, 
     0, 0, 1, 0, 0, 0, 0, 
     0, 1, 0, 1, 0, 0, 0,
     0, 0, 1,
 };//以空间换时间
 
// 输出一个解
 void Output(int a[], int n)
 {
    for(int i=0;i<n;i++)
	{
	  if(i==n-1)//坑爹的坑在这里，记住最后输出的没有空格，坑死在这里
      cout<<a[i];
	  else
      cout<<a[i]<<" ";
	}
     cout<<endl ;
 }
 
 // 判断当前序列是否满足条件
 bool IsOk(int a[], int lastIndex, int curValue)
 {
     if(lastIndex<0)//第一个元素没有前驱元素，返回真
         return true ;

     if(!((curValue+a[lastIndex]) & 1)) // 相邻的数奇偶性必然不同
         return false ;
 
     if(!prime[a[lastIndex]+curValue]) //相邻元素和为素数
         return false ;
 
     for(int i = 0; i <= lastIndex; i++) // 去重，curValue没有出现过
        if(a[i] == curValue)
         return false ;
 
     return true ;
 }
 
 void PrimeCircle(int a[], int n, int t)//在别的算法里，这里叫做dfs
 {
     if(n & 1)//奇数无解,直接返回
        return;
 
    if(t==n) 
     {
         if(prime[a[0]+a[n-1]])//判断首尾元素之和是否构成素数,刚才这里多了一个分号，仔细检查才发现，害人害个半死
             Output(a,n); 
     }
     else
     {
         for(int i=2;i<=n;i++)
         {
             a[t]=i;
             if(IsOk(a,t-1,i))//如果当前元素满足条件
             PrimeCircle(a,n,t+1);//进行下一次递归
         }
     }
 }
 
 int main()
 {
     int a[20],n,k=1;
     while(scanf("%d",&n)!=EOF)
	 {   
		 cout<<"Case "<<k<<":"<<endl;
		 k++;
		 a[0]=1;
		 PrimeCircle(a,n,1);
		 printf("\n");
	 }
     return 0 ;
 }