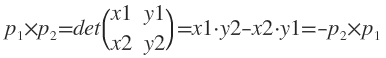判断平面上两条直线是否相交

首先引出计算几何学中一个最基本的问题：如何判断向量在的顺时针方向还是逆时针方向？

把p0定为原点，p1的坐标是(x1,y1)，p2的坐标是(x2,y2)。向量的叉积(cross product)实际上就是矩阵的行列式：

当叉积为正时，说明在的顺时针方向上；叉积为0说明两向量共线（同向或反向）。

当同时满足：

（1）和在的两侧（即一个顺时针方向上，一个在逆时针方向上）

（2）和在的两侧

时可肯定和相交。

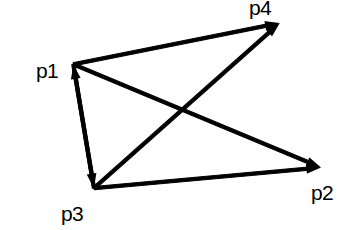
　　　　　　　　　　　　图1

图1是线段相交的一般情形。

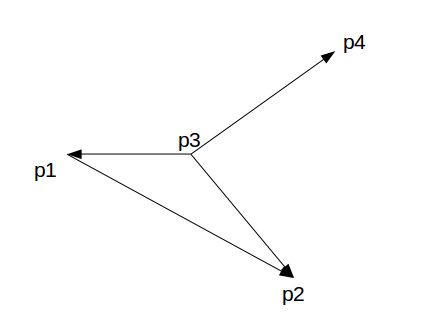
图2只满足第（1）条，不满足第（2）条所以不能证明和相交。

　　　　　　　　　　　　图2

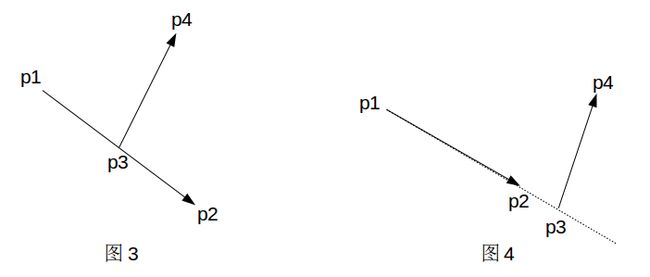
图3和图4是一种特殊情况，它不满足第（2）条，因为和重合,即和的叉积为0。

可见当叉积为0时要分情况讨论，当p3在线段p₁p₂上时两线段相交；当p3在线段p₁p₂的延长线上时两线段不相交。

double direction(pair<double,double> p1,pair<double,double> p2,pair<double,double> p3){
    pair<double,double> d1=make_pair(p3.first-p1.first,p3.second-p1.second);
    pair<double,double> d2=make_pair(p2.first-p1.first,p2.second-p1.second);
    return d1.first*d2.second-d1.second*d2.first;
}

direction函数用于计算和的叉积。

bool OnSegment(pair<double,double> p1,pair<double,double> p2,pair<double,double> p3){
    double x_min,x_max,y_min,y_max;
    if(p1.first<p2.first){
        x_min=p1.first;
        x_max=p2.first;
    }else{
        x_min=p2.first;
        x_max=p1.first;
    }
    if(p1.second<p2.second){
        y_min=p1.second;
        y_max=p2.second;
    }else{
        y_min=p2.second;
        y_max=p1.second;
    }
    if(p3.first<x_min || p3.first>x_max || p3.second<y_min || p3.second>y_max)
        return false;
    else
        return true;
}

当p3在直线p₁p₂上时，OnSegment函数用于确认p3在上，还是在的延长线上。

下面是用于判断两线段是否相交的主函数。

bool SegmentIntersect(pair<double,double> p1,pair<double,double> p2,pair<double,double> p3,pair<double,double> p4){
    double d1=direction(p3,p4,p1);
    double d2=direction(p3,p4,p2);
    double d3=direction(p1,p2,p3);
    double d4=direction(p1,p2,p4);

    if(d1*d2<0 && d3*d4<0)
        return true;
    else if(d1==0 && OnSegment(p3,p4,p1))
        return true;
    else if(d2==0 && OnSegment(p3,p4,p2))
        return true;
    else if(d3==0 && OnSegment(p1,p2,p3))
        return true;
    else if(d4==0 && OnSegment(p1,p2,p4))
        return true;
    else
        return false;
}

测试函数：

int main(){
    double x1,y1,x2,y2,x3,y3,x4,y4;
    cout<<"Please input x1,y1,x2,y2,x3,y3,x4,y4 by order"<<endl;
    cin>>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;
    pair<double,double> p1=make_pair(x1,y1);
    pair<double,double> p2=make_pair(x2,y2);
    pair<double,double> p3=make_pair(x3,y3);
    pair<double,double> p4=make_pair(x4,y4);
    if(SegmentIntersect(p1,p2,p3,p4))
        cout<<"YES"<<endl;
    else
        cout<<"NO"<<endl;
    return 0;
}