Java之数据结构基础、线性表、栈和队列、数组和字符串，树—学习笔记

                                                                          Java面试宝典之数据结构基础 —— 线性表篇

        本篇博文转载自：http://blog.csdn.net/zhangerqing/article/details/8796518；http://blog.csdn.net/zhangerqing/article/details/8822476；

       这部分内容作为计算机专业最基础的知识，几乎被所有企业选中用来作考题，因此，本章我们从本章开始，我们将从基础方面对数据结构进行讲解，内容主要是线性表，包括栈、队列、数组、字符串等，主要讲解基础知识，如概念及简单的实现代码，非线性结构我们在后面的文章中给出。

一、数据结构概念

    用我的理解，数据结构包含数据和结构，通俗一点就是将数据按照一定的结构组合起来，不同的组合方式会有不同的效率，使用不同的场景，如此而已。比如我们最常用的数组，就是一种数据结构，有独特的承载数据的方式，按顺序排列，其特点就是你可以根据下标快速查找元素，但是因为在数组中插入和删除元素会有其它元素较大幅度的移动，所以会带来较多的消耗，所以因为这种特点，使得数组适合：查询比较频繁，增、删比较少的情况，这就是数据结构的概念。数据结构包括两大类：线性结构和非线性结构，线性结构包括：数组、链表、队列、栈等，非线性结构包括树、图、表等及衍生类结构。本章我们先讲解线性结构，主要从数组、链表、队列、栈方面进行讨论，非线性数据结构在后面会继续讲解。

二、线性表

     线性表是最基本、最简单、也是最常用的一种数据结构。线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的。线性表的逻辑结构简单，便于实现和操作。因此，线性表这种数据结构在实际应用中是广泛采用的一种数据结构。其基本操作主要有：

 1）MakeEmpty(L) 这是一个将L变为空表的方法

   2）Length（L） 返回表L的长度，即表中元素个数 

   3）Get（L，i） 这是一个函数，函数值为L中位置i处的元素（1≤i≤n）

   4）Prev（L，i） 取i的前驱元素

   5）Next（L，i） 取i的后继元素

   6）Locate（L，x） 这是一个函数，函数值为元素x在L中的位置

   7）Insert（L，i，x）在表L的位置i处插入元素x，将原占据位置i的元素及后面的元素都向后推一个位置

   8）Delete（L，p） 从表L中删除位置p处的元素

   9）IsEmpty(L) 如果表L为空表(长度为0)则返回true，否则返回false

   10）Clear（L）清除所有元素

   11）Init（L）同第一个，初始化线性表为空

   12）Traverse（L）遍历输出所有元素

   13）Find（L，x）查找并返回元素

   14）Update（L，x）修改元素

   15）Sort（L）对所有元素重新按给定的条件排序

   16) strstr(string1,string2)用于字符数组的求string1中出现string2的首地址

   不管采用哪种方式实现线性表，至少都应该具有上述这些基本方法，下面我会将下数据结构的基本实现方式。

三、基础数据结构

    数据结构是一种抽象的数据类型（ADT），可以这么说，我们可以采用任意的方式实现某种数据结构，只要符合将要实现的数据结构的特点，数据结构就是一种标准，我们可以采用不同的方式去实现，最常用的两种就是数组和链表（包括单链表、双向链表等）。

数组是非常常见的数据类型，在任何一种语言里都有它的实现。

3.1我们这里采用Java来简单实现一下数组

数组是一种引用类型的对象，我们可以像下面这样的方式来声明数组：

int a[];
int[] b;
int []c;
a = new int[10];

总结起来，声明一个数组有基本的三个因素：类型、名称、下标，Java里，数组在格式上相对灵活，下标和名称可以互换位置，前三种情况我们可以理解为声明一个变量，后一种为其赋值。或者像下面这样，在声明的时候赋值：

int c[] = {2,3,6,10,99};
int []d = new int[10];

我稍微解释一下，其实如果只执行：int[] b,只是在栈上创建一个引用变量，并未赋值，只有当执行d = new int[10]才会在堆上真正的分配空间。上述第一行为静态初始化，就是说用户指定数组的内容，有系统计算数组的大小，第二行恰恰相反，用户指定数组的大小，由系统分配初始值，我们打印一下数组的初始值：

		int []d = new int[10];
		System.out.println(d[2]);

结果输出0，对于int类型的数组，默认的初始值为0.

但是，绝对不可以像下面这样：       int e[10] = new int[10];

无法通过编译，至于为什么，语法就是这样，这是一种规范，不用去想它。
我们可以通过下标来检索数组。下面我举个简单的例子，来说明下数组的用法。

	public static void main(String[] args) {
		String name[];
		name = new String[5];
		name[0] = "egg";
		name[1] = "erqing";
		name[2] = "baby";
		for (int i = 0; i < name.length; i++) {
			System.out.println(name[i]);
		}
	}

这是最简单的数组声明、创建、赋值、遍历的例子，下面写个增删的例子：

package com.xtfggef.algo.array;
public class Array {
	public static void main(String[] args) {
		int value[] = new int[10];
		for (int i = 0; i < 10; i++) {
			value[i] = i;
		}
		// traverse(value);
		// insert(value, 666, 5);
		delete(value, 3);
		traverse(value);
	}
	public static int[] insert(int[] old, int value, int index) {
		for (int k = old.length - 1; k > index; k--)
			old[k] = old[k - 1];
		old[index] = value;
		return old;
	}
	public static void traverse(int data[]) {
		for (int j = 0; j < data.length; j++)
			System.out.print(data[j] + " ");
	}
	public static int[] delete(int[] old, int index) {
		for (int h = index; h < old.length - 1; h++) {
			old[h] = old[h + 1];
		}
		old[old.length - 1] = 0;
		return old;
	}
}

简单写一下，主要想说明数组中删除和增加元素的原理：增加元素，需要将index后面的依次向后移动，然后将值插入index位置，删除则将后面的值依次向前移动，较简单。要记住：数组是表示相同类型的一类数据的集合，下标从0开始，就行了。

数组实现的线性表可以参考ArrayList，在JDK中附有源码，感兴趣的同学可以读读。

3.2下面我简单介绍下单链表

单链表是最简单的链表，有节点之间首尾连接而成，简单示意如下：

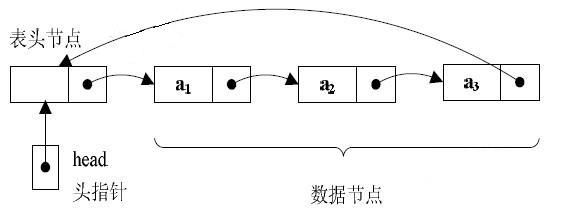
除了头节点，每个节点包含一个数据域一个指针域，除了头、尾节点，每个节点的指针指向下一个节点，下面我们写个例子操作一下单链表。

package com.xtfggef.algo.linkedlist;
public class LinkedList<T> {
	/**
	 * class node
	 * @author egg
	 * @param <T>
	 */
	private static class Node<T> {
		T data;
		Node<T> next;
		Node(T data, Node<T> next) {
			this.data = data;
			this.next = next;
		}
		Node(T data) {
			this(data, null);
		}
	}
	// data
	private Node<T> head, tail;
	public LinkedList() {
		head = tail = null;
	}
	/**
	 * judge the list is empty
	 */
	public boolean isEmpty() {
		return head == null;
	}
	/**
	 * add head node
	 */
	public void addHead(T item) {
		head = new Node<T>(item);
		if (tail == null)
			tail = head;
	}
	/**
	 * add the tail pointer
	 */
	public void addTail(T item) {
		if (!isEmpty()) { 
			tail.next = new Node<T>(item);
			tail = tail.next;
		} else { 
			head = tail = new Node<T>(item);
		}
	}
	/**
	 * print the list
	 */
	public void traverse() {
		if (isEmpty()) {
			System.out.println("null");
		} else {
			for (Node<T> p = head; p != null; p = p.next)
				System.out.println(p.data);
		}
	}
	/**
	 * insert node from head
	 */
	public void addFromHead(T item) {
		Node<T> newNode = new Node<T>(item);
		newNode.next = head;
		head = newNode;
	}
	/**
	 * insert node from tail
	 */
	public void addFromTail(T item) {
		Node<T> newNode = new Node<T>(item);
		Node<T> p = head;
		while (p.next != null)
			p = p.next;
		p.next = newNode;
		newNode.next = null;
	}
	/**
	 * delete node from head
	 */
	public void removeFromHead() {
		if (!isEmpty())
			head = head.next;
		else
			System.out.println("The list have been emptied!");
	}
	/**
	 * delete frem tail, lower effect
	 */
	public void removeFromTail() {
		Node<T> prev = null, curr = head;
		while (curr.next != null) {
			prev = curr;
			curr = curr.next;
			if (curr.next == null)
				prev.next = null;
		}
	}
	/**
	 * insert a new node
	 * @param appointedItem
	 * @param item
	 * @return
	 */
	public boolean insert(T appointedItem, T item) {
		Node<T> prev = head, curr = head.next, newNode;
		newNode = new Node<T>(item);
		if (!isEmpty()) {
			while ((curr != null) && (!appointedItem.equals(curr.data))) {
				prev = curr;
				curr = curr.next;
			}
			newNode.next = curr; 
			prev.next = newNode;
			return true;
		}
		return false; 
	}
	public void remove(T item) {
		Node<T> curr = head, prev = null;
		boolean found = false;
		while (curr != null && !found) {
			if (item.equals(curr.data)) {
				if (prev == null)
					removeFromHead();
				else
					prev.next = curr.next;
				found = true;
			} else {
				prev = curr;
				curr = curr.next;
			}
		}
	}
	public int indexOf(T item) {
		int index = 0;
		Node<T> p;
		for (p = head; p != null; p = p.next) {
			if (item.equals(p.data))
				return index;
			index++;

		}
		return -1;
	}
	/**
	 * judge the list contains one data
	 */
	public boolean contains(T item) {
		return indexOf(item) != -1;
	}
}

单链表最好玩儿的也就是增加和删除节点，下面的两个图分别是用图来表示单链表增、删节点示意，看着图学习，理解起来更加容易！

接下来的队列和栈，我们分别用不同的结构来实现，队列用数组，栈用单列表，读者朋友对此感兴趣，可以分别再用不同的方法实现。
四、队列
队列是一个常用的数据结构，是一种先进先出（First In First Out, FIFO）的结构，也就是说只能在表头进行删除，在表尾进行添加，下面我们实现一个简单的队列。

package com.xtfggef.algo.queue;
import java.util.Arrays;
public class Queue<T> {
	private int DEFAULT_SIZE = 10;	
	private int capacity;	
	private Object[] elementData;	
	private int front = 0;
	private int rear = 0;	
	public Queue()
	{
		capacity = DEFAULT_SIZE;
		elementData = new Object[capacity];
	}	
	public Queue(T element)
	{
		this();
		elementData[0] = element;
		rear++;
	}
	public Queue(T element , int initSize)
	{
		this.capacity = initSize;
		elementData = new Object[capacity];
		elementData[0] = element;
		rear++;
	}	
	public int size()
	{
		return rear - front;
	}
	public void add(T element)
	{
		if (rear > capacity - 1)
		{
			throw new IndexOutOfBoundsException("the queue is full!");
		}
		elementData[rear++] = element;
	}
        public T remove()
	{
		if (empty())
		{
			throw new IndexOutOfBoundsException("queue is empty");
		}
		
		@SuppressWarnings("unchecked")
		T oldValue = (T)elementData[front];
		
		elementData[front++] = null; 
		return oldValue;
	}  
    @SuppressWarnings("unchecked")
	public T element()  
    {  
        if (empty())  
        {  
            throw new IndexOutOfBoundsException("queue is empty");  
        }  
        return (T)elementData[front];  
    }  	
	public boolean empty()
	{
		return rear == front;
	}
	
	public void clear()
	{		
		Arrays.fill(elementData , null);
		front = 0;
		rear = 0;
	}
	public String toString()
	{
		if (empty())
		{
			return "[]";
		}
		else
		{
			StringBuilder sb = new StringBuilder("[");
			for (int i = front  ; i < rear ; i++ )
			{
				sb.append(elementData[i].toString() + ", ");
			}
			int len = sb.length();
			return sb.delete(len - 2 , len).append("]").toString();
		}
	}
	public static void main(String[] args){
		Queue<String> queue = new Queue<String>("ABC", 20);
		queue.add("DEF");
		queue.add("egg");
		System.out.println(queue.empty());
		System.out.println(queue.size());
		System.out.println(queue.element());
		queue.clear();
		System.out.println(queue.empty());
		System.out.println(queue.size());
	}
}

队列只能在表头进行删除，在表尾进行增加，这种结构的特点，适用于排队系统。

五、栈

栈是一种后进先出（Last In First Out，LIFO）的数据结构，我们采用单链表实现一个栈。

package com.xtfggef.algo.stack;
import com.xtfggef.algo.linkedlist.LinkedList;
public class Stack<T> {

	static class Node<T> {
		T data;
		Node<T> next;

		Node(T data, Node<T> next) {
			this.data = data;
			this.next = next;
		}

		Node(T data) {
			this(data, null);
		}
	}

	@SuppressWarnings("rawtypes")
	static LinkedList list = new LinkedList();

	@SuppressWarnings("unchecked")
	public T push(T item) {
		list.addFromHead(item);
		return item;
	}

	public void pop() {
		list.removeFromHead();
	}

	public boolean empty() {
		return list.isEmpty();
	}

	public int search(T t) {
		return list.indexOf(t);
	}

	public static void main(String[] args) {
		Stack<String> stack = new Stack<String>();
		System.out.println(stack.empty());
		stack.push("abc");
		stack.push("def");
		stack.push("egg");
		stack.pop();
		System.out.println(stack.search("def"));
	}
}

六、树

树形结构是一类重要的非线性结构。树形结构是结点之间有分支，并具有层次关系的结构。它非常类似于自然界中的树。树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；在数据库系统中，可用树来组织信息；在分析算法的行为时，可用树来描述其执行过程。本章重点讨论二叉树的存储表示及其各种运算，并研究一般树和森林与二叉树的转换关系，最后介绍树的应用实例。

七、二叉树

二叉树(BinaryTree)是n(n≥0)个结点的有限集，它或者是空集(n=0)，或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。关于更多概念，请大家自己上网查询，我们这里将用代码实现常见的算法。更多的概念，请访问：http://student.zjzk.cn/course_ware/data_structure/web/SHU/shu6.2.3.1.htm 。

1、二叉树的建立

首先，我们采用广义表建立二叉树（关于广义表的概念，请查看百科的介绍：http://baike.baidu.com/view/203611.htm）

我们建立一个字符串类型的广义表作为输入：

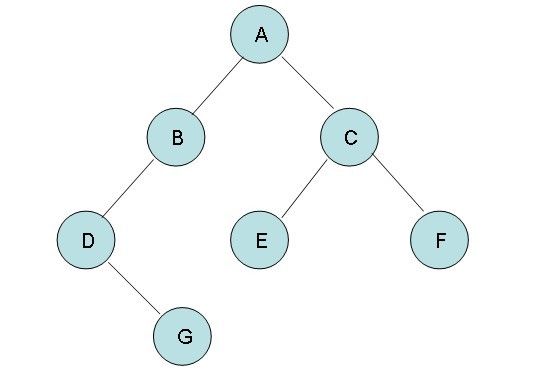
String  expression = "A(B(D(,G)),C(E,F))";与该广义表对应的二叉树为：

写代码前，我们通过观察二叉树和广义表，先得出一些结论：

• 每当遇到字母，将要创建节点
  
• 每当遇到“（”，表面要创建左孩子节点
• 每当遇到“，”，表明要创建又孩子节点
• 每当遇到“）”，表明要返回上一层节点
• 广义表中“（”的数量正好是二叉树的层数

根据这些结论，我们基本就可以开始写代码了。首先建议一个节点类（这也属于一种自定义的数据结构）。

package com.xtfggef.algo.tree;

public class Node {

	private char data;
	private Node lchild;
	private Node rchild;

	public Node(){
		
	}
	public char getData() {
		return data;
	}

	public void setData(char data) {
		this.data = data;
	}

	public Node getRchild() {
		return rchild;
	}

	public void setRchild(Node rchild) {
		this.rchild = rchild;
	}

	public Node getLchild() {
		return lchild;
	}

	public void setLchild(Node lchild) {
		this.lchild = lchild;
	}

	public Node(char ch, Node rchild, Node lchild) {
		this.data = ch;
		this.rchild = rchild;
		this.lchild = lchild;
	}

	public String toString() {
		return "" + getData();
	}
}

根据广义表创建二叉树的代码如下：

public Node createTree(String exp) {
		Node[] nodes = new Node[3];
		Node b, p = null;
		int top = -1, k = 0, j = 0;
		char[] exps = exp.toCharArray();
		char data = exps[j];
		b = null;
		while (j < exps.length - 1) {
			switch (data) {
			case '(':
				top++;
				nodes[top] = p;
				k = 1;
				break;
			case ')':
				top--;
				break;
			case ',':
				k = 2;
				break;
			default:
				p = new Node(data, null, null);
				if (b == null) {
					b = p;
				} else {
					switch (k) {
					case 1:
						nodes[top].setLchild(p);
						break;
					case 2:
						nodes[top].setRchild(p);
						break;
					}
				}
			}
			j++;
			data = exps[j];
		}
		return b;
	}

思路不难，结合上述的理论，自己断点走一遍程序就懂了！

2、二叉树的递归遍历

二叉树的遍历有三种：先序、中序、后序，每种又分递归和非递归。递归程序理解起来有一定的难度，但是实现起来比较简单。对于上述二叉树，其：

    a 先序遍历

            A B D G C E F

    b 中序遍历

           D G B A E C F 

    c 后序遍历

           G D B E F C A

先、中、后序递归遍历如下：

/**
	 * pre order recursive
	 * 
	 * @param node
	 */
	public void PreOrder(Node node) {
		if (node == null) {
			return;
		} else {
			System.out.print(node.getData() + " ");
			PreOrder(node.getLchild());
			PreOrder(node.getRchild());

		}
	}

	/**
	 * in order recursive
	 * 
	 * @param node
	 */
	public void InOrder(Node node) {
		if (node == null) {
			return;
		} else {
			InOrder(node.getLchild());
			System.out.print(node.getData() + " ");
			InOrder(node.getRchild());
		}
	}

	/**
	 * post order recursive
	 * 
	 * @param node
	 */
	public void PostOrder(Node node) {
		if (node == null) {
			return;
		} else {
			PostOrder(node.getLchild());
			PostOrder(node.getRchild());
			System.out.print(node.getData() + " ");
		}
	}

二叉树的递归遍历实现起来很简单，关键是非递归遍历有些难度，请看下面的代码：

3、二叉树的非递归遍历

先序非递归遍历：

public void PreOrderNoRecursive(Node node) {
		Node nodes[] = new Node[CAPACITY];
		Node p = null;
		int top = -1;
		if (node != null) {
			top++;
			nodes[top] = node;
			while (top > -1) {
				p = nodes[top];
				top--;
				System.out.print(p.getData() + " ");
				if (p.getRchild() != null) {
					top++;
					nodes[top] = p.getRchild();
				}
				if (p.getLchild() != null) {
					top++;
					nodes[top] = p.getLchild();
				}
			}
		}
	}

原理：利用一个栈，先序遍历即为根先遍历，先将根入栈，然后出栈，凡是出栈的元素都打印值，入栈之前top++，出栈之后top--，利用栈后进先出的原理，右节点先于左节点进栈，根出栈后，开始处理左子树，然后是右子树，读者朋友们可以自己走一遍程序看看，也不算难理解！

中序非递归遍历：

public void InOrderNoRecursive(Node node) {
		Node nodes[] = new Node[CAPACITY];
		Node p = null;
		int top = -1;
		if (node != null)
			p = node;
		while (p != null || top > -1) {
			while (p != null) {
				top++;
				nodes[top] = p;
				p = p.getLchild();
			}
			if (top > -1) {
				p = nodes[top];
				top--;
				System.out.print(p.getData() + " ");
				p = p.getRchild();
			}
		}
	}

原理省略。

后续非递归遍历：

public void PostOrderNoRecursive(Node node) {
		Node[] nodes = new Node[CAPACITY];
		Node p = null;
		int flag = 0, top = -1;
		if (node != null) {
			do {
				while (node != null) {
					top++;
					nodes[top] = node;
					node = node.getLchild();
				}
				p = null;
				flag = 1;
				while (top != -1 && flag != 0) {
					node = nodes[top];
					if (node.getRchild() == p) {
						System.out.print(node.getData() + " ");
						top--;
						p = node;
					} else {
						node = node.getRchild();
						flag = 0;
					}
				}
			} while (top != -1);
		}
	}

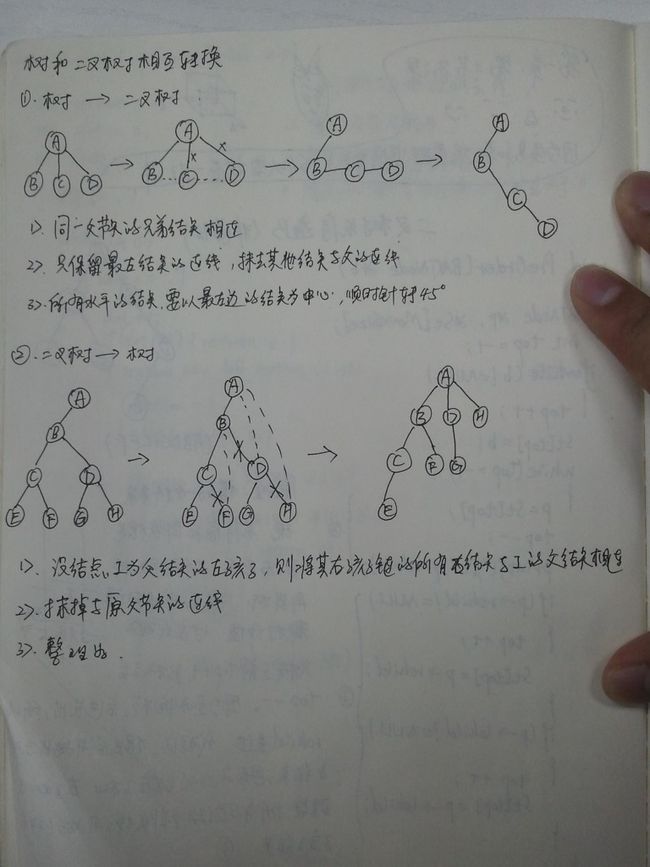
八、树与二叉树的转换

本人之前总结的：

以上博文转载自：http://blog.csdn.net/zhangerqing/article/details/8796518；http://blog.csdn.net/zhangerqing/article/details/8822476；

仅供自己学习参考之用！