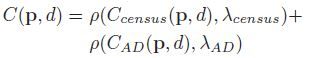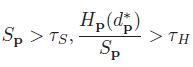Stereo Matching文献笔记之(八):《On Building an Accurate Stereo Matching System on Graphics Hardware》读后感~
周末喽~!又有时间写写博客了,继续之前的论文读后感,我发现写博客有好几个好处:1.分享。2.备忘。3.锻炼表达能力。不知道有没有童鞋和我有一样的结论,今天写写今年四月份精读过的一篇文章《On Building an Accurate Stereo Matching System on Graphics Hardware》,文章名咋看起来有点像硬件相关文献,为什么叫做一个系统,我想可能是由于作者来自于企业的研究院才这么起名的,但说出它的别名大家就都知道了,就是AD-Census,这是2011年提出来的算法,作者与SegmentTree是同一人,引用率颇高哈!言归正传,本文说一说我对AD-Census的理解,理解不正确的地方,还请各位童鞋批评指正!!
(转载请注明:http://blog.csdn.net/wsj998689aa/article/details/49403353, 作者:迷雾forest)
算法详解
这篇文章的亮点我认为有三处:1. 适合并行;2. 基于特征融合的代价计算;3. 基于自适应区域的代价聚合;下面就这几个方面详细说一说。
1. 适合并行
这点是相当吸引人的,也是作者的出发点,众所周知,全局算法不适合并行,为啥?因为建立了复杂而且漂亮的能量函数,需要用同样复杂而且漂亮的迭代优化算法求解,可惜的是这样的优化算法如果想并行处理难度太高,并且也快不到哪里去,所以导致现有很多全局算法无法得到应用,我们只能眼睁睁的看着middlebery上的顶级算法,一边淌着哈喇子,一边望洋兴叹。不过本文关于并行这块的解释就不多说了,不亲自动手实现是无法体会出来并行带来的快感。所以主要说说对下面两点的理解,要知道AD-Census就算拼效果也是得过头把交椅的。。。
2. 特征融合
我看过的文献中,很少有在代价计算这一步中融合多种特征的,一般只采用一种特征而已并且对这块内容的研究也偏少,作者另辟蹊径的融合了现有特征AD和Census,AD就是最普通的颜色差的绝对值,立体匹配算法中经常使用,其公式如下所示:
其中,i代表不同的通道,这个公式相信大家肯定都一目了然,根据左右两图的颜色差的大小来定义cost,这里值得一提的是几个名词:reference image,base image,guidance image和match image,我之前就被绕晕过,因为不同的论文总喜欢用不同的词汇来代表左图和右图,reference image一般翻译成为参考图像,base image和guidance image就是reference image,一般被翻译成为基准图像,match image一般被翻译成为匹配图像,那么参考图像和匹配图像的关系是什么呢?我真的好想说,不就是一个代表左图一个代表右图嘛!!!但是咱们是搞研究的,必须要严谨一些才行,我们回忆一下立体匹配的流程,左图和右图先做代价计算,怎么做的呢,遍历左图中的每一个像素,然后根据视差范围中的每一个视差值,来找到对应右图的像素,然后根据公式计算代价,然后再针对左图,遍历每个像素进行代价聚合计算,这就是重点,如果你在左图上计算代价聚合,那么左图就叫做参考图像,右图就是匹配图像,反之,就反过来叫。。。
话说回来,Census指的是一种代价计算方法,其属于非参数代价计算方法中的一种(另外一个代表是rank transform),准确的说它是一种距离度量,它的计算过程的前半部很像经典的纹理特征LBP,就是在给定的窗口内,比较中心像素与周围邻居像素之间的大小关系,大了就为1,小了就为0,然后每个像素都对应一个二值编码序列,然后通过海明距离来表示两个像素的相似程度,Census代码如下所示:
int hei = lImg.rows;
int wid = lImg.cols;
Mat lGray, rGray;
Mat tmp;
lImg.convertTo( tmp, CV_32F );
cvtColor( tmp, lGray, CV_RGB2GRAY );
lGray.convertTo( lGray, CV_8U, 255 );
rImg.convertTo( tmp, CV_32F );
cvtColor( tmp, rGray, CV_RGB2GRAY );
rGray.convertTo( rGray, CV_8U, 255 );
// prepare binary code
int H_WD = CENCUS_WND / 2;
bitset<CENCUS_BIT>* lCode = new bitset<CENCUS_BIT>[ wid * hei ];
bitset<CENCUS_BIT>* rCode = new bitset<CENCUS_BIT>[ wid * hei ];
bitset<CENCUS_BIT>* pLCode = NULL;
bitset<CENCUS_BIT>* pRCode = NULL;
// 代价计算
// 计算左图
for(int i = 0; i < reflect_pts_num; i++)
{
int repeated = reflect[i].repeated;
if(repeated == 1)
{
continue;
}
int x = reflect[i].x;
int y = reflect[i].y;
int index = reflect[i].index;
uchar pLData = lGray.at<uchar>( y, x );
pLCode = &(lCode[index]);
int bitCnt = 0;
for( int wy = - H_WD; wy <= H_WD; wy ++ )
{
int qy = ( y + wy + hei ) % hei;
for( int wx = - H_WD; wx <= H_WD; wx ++ )
{
if( wy != 0 || wx != 0 )
{
int qx = ( x + wx + wid ) % wid;
uchar qLData = lGray.at<uchar>( qy, qx );
( *pLCode )[bitCnt] = ( pLData > qLData );
bitCnt ++;
}
}
}
}
// 计算右图
pRCode = rCode;
for( int y = 0; y < hei; y ++ ) {
uchar* pRData = ( uchar* ) ( rGray.ptr<uchar>( y ) );
for( int x = 0; x < wid; x ++ ) {
int bitCnt = 0;
for( int wy = - H_WD; wy <= H_WD; wy ++ ) {
int qy = ( y + wy + hei ) % hei;
uchar* qRData = ( uchar* ) ( rGray.ptr<uchar>( qy ) );
for( int wx = - H_WD; wx <= H_WD; wx ++ ) {
if( wy != 0 || wx != 0 ) {
int qx = ( x + wx + wid ) % wid;
( *pRCode )[ bitCnt ] = ( pRData[ x ] > qRData[ qx ] );
bitCnt ++;
}
}
}
pRCode ++;
}
}
// 代价体计算
bitset<CENCUS_BIT> lB;
bitset<CENCUS_BIT> rB;
for(int i = 0; i < reflect_pts_num; i++)
{
int repeated = reflect[i].repeated;
if(repeated == 1)
{
continue;
}
int x = reflect[i].x;
int y = reflect[i].y;
int index = reflect[i].index;
lB = lCode[index];
for(int d = 0; d < maxDis; d ++)
{
if(x - d >= 0)
{
rB = rCode[ index - d ];
costVol[d].at<double>(y, x) = ( lB ^ rB ).count();
}
else
{
costVol[d].at<double>(y, x) = CENCUS_BIT;
}
}
}
那为什么融合起来效果就会好呢?
这个是重点,Census具有灰度不变的特性,所谓灰度不变指的就是像素灰度值的具体大小和编码之间的相关性不是很强,它只关心像素之间的大小关系,即使你从5变成了10,但只要中心像素是15,就一点事情都木有,这样的性质我们肯定会想到它一定对噪声和鲁棒,的确是这样。但是它的缺点也很明显,按照文章的说法, 对于结构重复的区域这个特征就不行了,那基于颜色的特征AD呢?它是对颜色值很敏感的,一旦区域内颜色相近(低纹理)或者有噪声那么挂的妥妥的,但是对重复结构却不会这样,基于这种互补的可能性,作者尝试将二者进行融合,这是一种很简单的线性融合但是却取得了很好的效果:
其中,下面公式的目的就是归一化,我们注意看,两种计算方法得到的取值范围可能会相差很大,比如一个取值1000,另一个可能只取值10,这样便有必要将两者都归一化到[0,1]区间,这样计算出来的C更加有说服力,这是一种常用的手段。论文中给出了AD,Census,AD-Census对一些细节处理的效果图,可以看得出来各自的优缺点,第一行是重复纹理区域,第二行是低纹理区域,白色与黑色都说明计算的结果很差。
下面分别给出AD、Census、AD-Census的效果图,正如上一大段的分析,我们会发现AD往往比Census在物体边缘上的处理更好一些,边缘明显清晰,但是AD得到的噪声太多,并且在低纹理区域,比如中间那个灯罩,AD出现了很大的空洞,在这一点上Census做的相对较好,AD-Census在物体边缘上的效果是二者的折中,但噪声更少,整体效果更加理想。
3. 自适应区域
这块内容是该文献的重点,再说之前我们先回顾一下一般的代价聚合思想,局部算法采用一个固定或者自适应窗口来代价聚合,全局算法采用整幅图像得到的抽象结构来代价聚合,例如MST,马尔科夫图模型等等,这些在之前的博客都描述过,我们总结一下二者的共同点,不就是事先确定一个有意义的区域吗?确定好了之后便可直接在这个区域内进行代价聚合,OK!统一了思想,就可以说说这篇文章是怎么做的了。
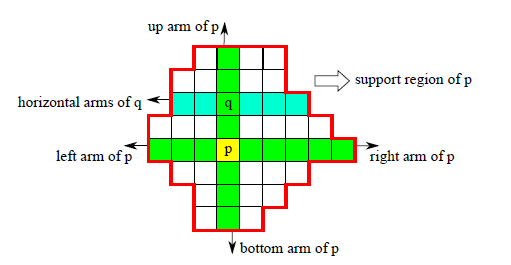
ADCensus建立了一个灰常有意思的,工程化的区域结构,分割算法耗时不舍得用,干脆我直接用相对暴力的方案对图像进行分割好了,看图说话,下图就是作者采用的分割方法:
采用方法的思想很简单,当前像素假设是p,我对p先进行垂直方向的遍历,如果像素q满足两个约束,那么就算同一分割区域,否则遍历停止,然后再在得到的N个q和p的水平方向根据同样的规则进行遍历,于是就得到了对应的分割区域。然而,作者从来都没有说对图像进行了分割,只是说确定p的cross,其实就是分割的意思。约束如下所示,这个约束是经过改造过的(cross region不是作者提出来的,也是引用他人的方法,作者对约束从两个扩充为三个),这么改的原因是作者考虑到了之前的约束方案会导致将边缘点也包括进去,这样会对边缘的视差计算十分不利,于是提出了一个更加严格的约束形式,考虑到了相邻像素色彩上的差异。
下面就可以在像素所属的区域内进行代价聚合了,就是简单地将区域内各个像素的ADCensus值相加,但是这里有个很大的问题作者说的很模糊,作者在文章中强调,为了保证代价聚合的稳定性,需要进行“先水平后垂直”,“先垂直后水平”两种代价聚合方案各两次。我当时很迷糊,因为我认为一旦每个像素所属的区域确定了,这两种方案得到的代价聚合值肯定是一样的,除非作者在构建区域的时候,也是采用“先水平后垂直”,“先垂直后水平”的方案,根据我这个猜想还写了代码做了实验,结果发现效果一般,并且反复的看文献,发现作者说的很明确,就是代价聚合的时候采用两种方案,而不是区域构建的时候,这到底是怎么回事?
忽然有一天秋叶旁落,我终于明白了作者的意图,别忘记了,我们还有一幅图像呢,就是右图!!!这么重要的线索我竟然忽略了,答案是要对左图和右图分别进行区域构建,然后代价聚合的时候,如果采用“先水平后垂直”的方案,那么就先取左右两个对应区域的交集,然后在将交集中的代价值都加起来,进一步计算垂直方向的代价值的和。另一种方案就是先垂直方向的区域相交,再水平求和,这样就能得到不同的代价聚合结果。两种方案各自执行两次,每一次都用之前新得到的代价聚合值,注意这里作者只是简单的将区域内各像素对应的代价值相加,没有考虑到权值,可能是为了速度吧,当然加上权值效果肯定会更加好一些。
上图是代价聚合的过程,是先水平后垂直的方案,代价聚合之后,对于一般的局部算法而言,基本上就到此为止了,但是ADCensus还有一个大招呼之欲来,那就是大名鼎鼎的“扫描线优化”,这个扫描线优化是动态规划的一种方法,在史上最经典立体匹配文献SGM中首次被使用,具体的思想本文就不详细说了,由于代价聚合的结果不大靠谱,可以考虑将其视作数据项,建立全局能量函数(公式如下所示),这样便直接过渡到了全局算法。
其中,第一项C就是代价聚合项,后面两项分别考虑到了视差的微变(低纹理区域)和剧烈变化(物体边缘),优化这个能量函数做采用的方法就是“扫描线优化法”,其公式如下所示,这里和SGM一模一样,不做过多的解释,因为以后还会和大家聊聊我对SGM的理解。
然而,ADCensus在P1和P2的设定上不同于SGM,进行了调整,具体的公式就不再粘贴了。做了实验,如下三幅图所示,左图是直接利用代价聚合得到的视差图,中间一副是进一步通过扫描线优化之后得到的视差图,第三幅图是二者的差异,蓝色代表差异微弱,红色代表差异较大,黑色代表没有差异,可以明显看到,经过扫描线优化处理之后,视差图在细节上明显处理的更好,边缘更加平滑,但是出现了拖尾现象(灯杆子那里)。
后续
和其他文献相同,作者也采用left-right-check的方法将像素点分类成为三种:遮挡点,非稳定点,稳定点。对于遮挡点和非稳定点,只能基于稳定点的视差传播来解决,本文在视差传播这一块采用了两种方法,一个是迭代区域投票法,另一个是16方向极线插值法,后者具体来说:沿着点p的16个方向开始搜索,如果p是遮挡点,那么遇到的第一个稳定点的视差就是p的视差,如果p是非稳定点,那么遇到第一个与p点颜色相近的稳定点的视差作为p的视差。针对于视差图的边缘,作者直接提取两侧的像素的代价,如果有一个代价比较小,那么就采用这个点的视差值作为边缘点的视差值,至于边缘点是如何检测出来的,很简单,对视差图随便应用于一个边缘检测算法即可。做完这些之后,别忘记亚像素求精,这和WTA一样,是必不可少的。流程图如下,忘记说了,再来一个中值滤波吧,因为大家都这么玩,属于后处理潜规则。。
这里重点说说迭代区域投票法,这是我自己的翻译,英文称呼是“Iterative Region Voting”,它的目的是对outlier进行填充处理,一般来说outlier遮挡点居多,之前的博客也介绍过,填充最常用的方法就是用附近的稳定点就行了,省时省力,就是不利于并行处理,作者要设计的是一个完全适合GPU编程的算法,所以采用了迭代区域投票法,具体做法是对之前区域构建所得到的每个区域求取视差直方图(不要归一化),例如,得到的直方图共有15个bin,最大的bin值是8,那么outlier的视差就由这个8来决定,但是稳定点的个数必须得比较多,比较多才有统计稳定性,数学形式化就是如下公式:
其中,Sp就是稳定点的个数,Hp就是最大bin值,一般Ts,Th两个参数都经验设定,说白了就是得好好调试一番。此外,这个方法是迭代的,这只是针对稳定点个数具有统计意义的区域,有些outlier由于区域内稳定点个数不满足公式,这样的区域用此方法是处理不来的,只能进一步通过16方向极线插值来进一步填充,二者配合起来能够取得不错的效果,自己做了实验,这两种方法的顺序也必须一先一后,否则效果也不行,说明一个是大迂回战略,目的是消灭有生力量,一个是歼灭战,打的是漏网之鱼,二者珠联璧合,可喜可贺。
总结
ADCensus是个好算法!简单易于实现,完全有利于并行处理,具有实用化价值,大家可以动手编码试一试,文章里面也提供了并行计算指导。这就是我的理解,如有错误请不吝赐教哈~
不过我对这篇论文有个疑问,就是在自适应区域那里,为什么作者偏偏要加上一个自适应区域内代价聚合呢?总所周知,SGM中没有这一个步骤,并且自适应区域其实就是分割的目的,在区域内代价聚合并没有设置每个像素匹配代价之前的权值,如果我们将自适应区域这一步去掉,其实ADCensus和SGM唯一的区别就只有匹配代价的计算方式了,前者不用多说,本文解释了是一种融合代价,后者采用的或是BT或是互信息,莫非融合特征就必须伴随自适应区域??未来有空闲我便会重新编码去究其原因,最近琅琊榜实在是看多了,抱着怀疑一切的态度也开始怀疑上了作者的动机,根据我的猜测,原因无外乎有三种。
1. 自适应区域确实有用,没有了它视差图效果就会大打折扣,所谓正途。
2. 自适应区域是为了发表论文才加上去的,如果没有这一块,论文的表面含金量就缩水了,所谓鸡肋。
3. 自适应区域的真实目的是为了后续的迭代区域求精,所以索性也用于代价聚合,所谓醉翁之意不在酒。
不知是否有童鞋也有同样的疑问,还请不吝赐教。