hdu 3511 Prison Break 圆 扫描线
Prison Break
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 1850 Accepted Submission(s): 563
The prison consists of many circular walls. These walls won't intersect or tangent to each other.
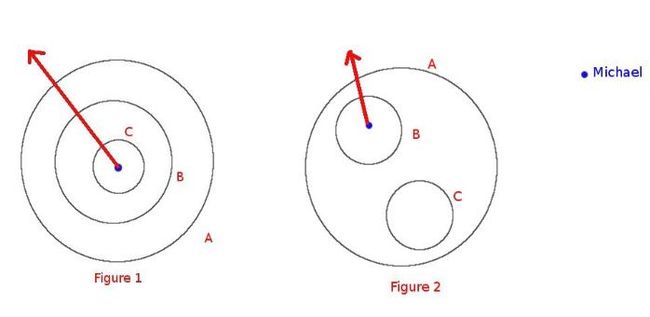
Now Michael is arrested in one of the deepest rooms, and he wants to know how many walls he has to break at least for running out. In figure 1, Michael has to break 3 walls at least and in figure 2, 2 walls are needed.
For each test case, the first line contains one number: n (1<=n<=50,000) indicating the total number of circular walls.
Then n lines follow, each line contains three integers x, y, r. (x,y) indicates the center of circular wall and r indicates the radius of the wall.
-100,000<=x,y<=100,000
1 <= r <= 100,000
The input ends up with EOF.
3 0 0 1 0 0 2 0 0 3 3 0 0 10 5 0 1 -5 0 1
3 2
题意:
给出很多个圆,没有相切,相交,只有相容和相离的情况。求一个圆被其他圆包围的个数,最多是多少?就是求圆的深度。
方法:
扫描线的方法是N*long(N)的
假设圆是按照圆心的x坐标排序的。有一条扫描线x = z 会与很多圆相交于两个点,分别对应于这个圆的上半圆和下半圆。交点从上到下是顺序的,当扫描线继续向前移动的时候,这种相对顺序是不会改变的。此时如果再加入新的扫描线与其他圆的交点情况,只要把扫描线x代入每个圆中,计算得到y的坐标,然后在这个位置上插入该点即可。
用线性的数据结构是比较难以实现的,因为交点的y坐标会改变。但是如果采用的是树形结构,那么容易理解,树上的结点的相对顺序不会改变。插入一个点的时候,只要比较两个结点当前的大小,就可以在一个位置上插入该点了。
STL中的set其实也是个树形结构,只需要对比较函数做一些修改就可以实现了。
方法:
STL结点记录的圆的id信息,以及在比较函数中,计算的y是对应是圆的上部分还是下部分。修改比较函数的输入是(id,ty)
定义全局变量globalx 表示扫描线当前的x坐标。 把globalx代入方程求得扫描线与圆id的交点,如果ty=1取上半圆的交点。
通过计算得到y1,y2再比较大小即可。 因为圆不想交,对于任何一个globalx的值,除了id值一样外,不能得到y1,y2的值是一样的。所以id一样时,判断ty的大小即可。
扫描线的扫描顺序是x从大到小。首先将圆的左顶点和右顶点加入数组中,然后对这个数组进行排序,就是扫描线的前进取值方式了。
对于一个点,如果是左顶点,则加入点(id,1)到set中,然后查看这个点上方和下方的点情况:
1. 上下点属于同一个圆,那么该圆就是当前圆的直接包含的圆了
2. 没有上面的点,或者没有下面的点,说明这个圆是最外围的圆
3. 上下点属于不同的圆,那么深度大的那个圆就是当前圆的兄弟,另一个便是当前圆的直接包含圆了
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<set>
#include<cstring>
#include<vector>
#include<math.h>
using namespace std;
#define maxn 100010
struct Circle{
int id,x,r,y;
Circle(int _id=0,int _x=0,int _y=0){
id=_id, x=_x, y=_y;
}
};
Circle cir[maxn];
//用于对圆的左右端点排序
Circle p[maxn];
int cmp(Circle a,Circle b){
return a.x < b.x;
}
//用于扫面的位置排序,globalx是当前扫描线的位置
int globalx;
//记录扫描线的交点信息ty = 1表示上交点
struct Point{
int id,ty;
Point(int _id=0,int _ty=0){
id = _id;
ty = _ty;
}
};
//计算圆id在x=globalx时的y坐标
double yposition(int id,int ty){
double x = globalx - cir[id].x;
double y = sqrt(cir[id].r*1.0*cir[id].r-x*x);
if(ty == 1) return y+cir[id].y;
return cir[id].y-y;
}
//扫描线与圆的交点按y从大到小排序
bool operator < ( Point a, Point b) {
if(a.id == b.id)
return a.ty > b.ty;
return yposition(a.id,a.ty) > yposition(b.id,b.ty);
}
set<Point> haha;
int fa[maxn];
int dep[maxn];
int main(){
int n,f;
while(scanf("%d",&n)!=EOF){
for(int i = 0;i < n; i++){
scanf("%d%d%d",&cir[i].x,&cir[i].y,&cir[i].r);
p[i*2] = Circle(i,cir[i].x-cir[i].r,0);
p[i*2+1] = Circle(i,cir[i].x+cir[i].r,1);
}
int nn = 2 * n;
sort(p,p+nn,cmp);
haha.clear();
set<Point>::iterator it1,it2;
memset(dep,0,sizeof(dep));
int ans = 0;
for(int i = 0;i < nn; i++){
globalx = p[i].x;
if(p[i].y == 1){
haha.erase(Point(p[i].id,0));
haha.erase(Point(p[i].id,1));
}
else {
it1 = haha.insert(Point(p[i].id,1)).first;
it2 = it1;
it1++;
if(it1 == haha.end() || it2 == haha.begin()){
//fa[p[i].id] = f =n;
dep[p[i].id] = 1;
}
else {
it2--;
if(it2->id == it1->id){
dep[p[i].id] = dep[it1->id]+1;
}
else
dep[p[i].id] = max(dep[it2->id],dep[it1->id]);
}
haha.insert(Point(p[i].id,0));
}
ans = max(ans,dep[p[i].id]);
}
printf("%d\n",ans);
}
return 0;
}
/*
3
0 0 1
0 0 2
0 0 3
3
0 0 10
5 0 1
-5 0 1
3
0 0 100
80 80 10
88 88 1
5
0 0 100
0 1 1
0 4 1
0 9 1
3 0 1
*/