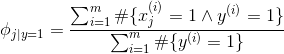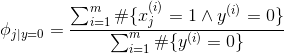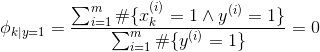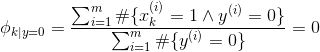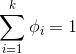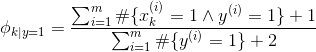机器学习--朴素贝叶斯



本文转自：http://blog.csdn.net/linkin1005/article/details/39025879

首次听说朴素贝叶斯是在吴军的google黑板报数学之美专题，统计语言模型一章中谈及。其后，吴信东在我们学院的《数据挖掘十大算法》中再次介绍。最近，在学习Andrew Ng的机器课程也介绍了朴素贝叶斯。既然这么重要，有必要将课程内容进行整理。

一、  概念

1)     贝叶斯模型

贝叶斯模型是将两个事件之间的先验概率和后验概率建立起一座桥梁，即已知可以求出：

现实中生活中，我们有时不知道在事件A发生的情况下，事件B发生的概率。比如我们有一个病人的体检参数（A），但我门不知道他患有癌症的概率，但是我们有历史数据，知道在特定的体检参数条件下，病人患有癌症的概率，根据贝叶斯公式和全概率公示，我们能够推断出。

2)     朴素贝叶斯（Naive Bayesian Model）

朴素贝叶斯模型假设训练样本的各特征之间相互独立，这样的假设称为朴素贝叶斯假设（Naive bayes assumption），一般来说，这样的假设是不成立，的而该分类算法被称为朴素贝叶斯分类器（Naive bayes classifier）。

二、  应用领域

朴素贝叶斯分类器是一种离散特征值的分类方法（在机器学习领域，XX机，XX器都是XX算法的意思，起这样的名字可能是想突出这样的方法处理问题更加自动化，无需人工干预）,可以进行二分类，也可以进行多值分类。

三、  模型

输入：m个训练样本，其中，即分k个类

方法：计算所有类别的概率，计算每个特征属性的所有划分的条件概率，即所有的。

输出：计算所有的，最大的一项即为未知样本X所属的类别。（其实也就是计算，由于P (X)对于所有的样本均相等，因此可以省略）

四、  实例——垃圾邮件分类

目的：假设我们有一个邮件的文本，我们希望能够判断它是垃圾邮件还是非垃圾邮件。

样本：我们有一批（m个）已经标识为垃圾邮件(y=1)和非垃圾邮件(y=0)的邮件文本。还有相应的字典，字典是有序排列的，包括所有单词。

步骤：

a)       构建空特征向量，，向量长度为字典长度；

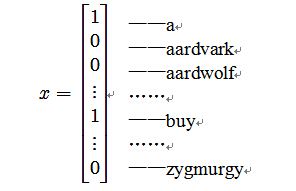
b)      根据邮件中各单词所在的字典位置，将相应位置的赋值为1；如下所示

这个矩阵的表示这封邮件中有单词a和buy，但不包含单词aardvark、aardwolf和zygmurgy。

c)       由于样本为已经分好类的邮件，因此可得：

                                                                         

                                                                     

                                                                     

                                                                       

由步骤1到步骤2使用的就是朴素贝叶斯假设。

d)       令，它表示的是在该邮件被标为垃圾邮件的前提下，位置i下的单词出现的概率；，表示在该邮件被标为非垃圾邮件的前提下，位置i下的单词出现的概率。，表示一个邮件被标记为垃圾邮件的概率。

训练样本的联合概率为：

求此最大似然方程，可得参数：

其中，符号“”表示逻辑“与”，符号“#”表示符合集合中给定条件的样本个数。

e)       假设一个新的样本，其特征值为x，那么就可以计算它为垃圾邮件的概率：

                                                                       

                                                                   

                                                                   

                                                                   

而它不是垃圾邮件的概率就为1-比较这两个概率值大小，就可以确定该邮件是否为垃圾邮件。

五、  拉普拉斯平滑（Laplace smoothing）

上文提及的垃圾邮件分类器中，可以利用训练样本进行参数估计，从而构建出一个垃圾邮件分类器，可以将新的未标识的邮件进行分类。但是，假如一个字典中在位置k的单词从未出现在训练样本中，会有：

如果我们将一个含有该单词的未标识邮件放入我们构建的垃圾邮件分类器，会得到这样的结果：

                                                                                 

                                                                            

                                                                            

                                                                            

答案为未定型，因而不能判断该邮件是否为垃圾邮件，分类器失效！

解决办法是引入一种方法，将训练样本中出现过的词的发生概率让渡一部分给从未出现的词。

假设需要将样本分为k个类，那么类的集合可以表示为，令，假设m个训练样本的分类标号分别为，可得：

如果某些类型没有在训练样本中出现，那么存在。我们可以用拉普拉斯平滑来解决这样的问题：

我们将分母加上1，分子加上k，此时，所有的，但是并不改变所有概率和为1的性质：。

再回到邮件分类器：利用拉普拉斯平滑方法就可以对样本中从未出现的单词进行参数估计：