usaco Closed Fences
本来这道题目却被不想写的,因为方法有点麻烦。
不过最后还是耐下性子写了。呜……
思路是挺简单的。
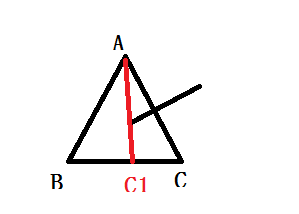
设观察位置为A,BC为多边形上的一条边。若有边挡住了A点的视线,刚更新A当前的视野。
如下图:
此时视野为BC1
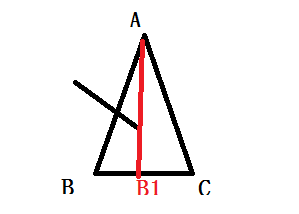
此时视野为B1C
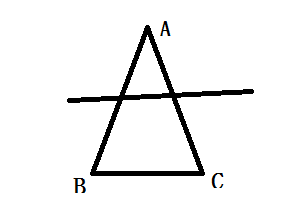
此时被完全挡住,没有视野。
代码如下:
/*
ID: guo geer
PROG: fence4
LANG: C++
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
#define les 1e-6
struct Point{int x, y;};
Point P[300],ob;
int res[300];
double x,y;//交点
double cross(double x1,double y1,double x2,double y2,double x,double y)
{
return (x1-x)*(y2-y)-(x2-x)*(y1-y);
}
int intersection(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
if(cross(x2,y2,x3,y3,x1,y1)==0&&cross(x2,y2,x4,y4,x1,y1)==0)
return 0;
if(cross(x2,y2,x3,y3,x1,y1)*cross(x2,y2,x4,y4,x1,y1)<=les&&cross(x4,y4,x1,y1,x3,y3)*cross(x4,y4,x2,y2,x3,y3)<=les)
return 1;
return 0;
}
int isInTriangle(double x1,double y1,double x2,double y2,double x3,double y3,double x,double y)
{
double x0,y0;
x0=(x1+x2+x3)/3;
y0=(y1+y2+y3)/3;
if(cross(x1,y1,x0,y0,x2,y2)*cross(x1,y1,x,y,x2,y2)<=les) return 0;
if(cross(x2,y2,x0,y0,x3,y3)*cross(x2,y2,x,y,x3,y3)<=les) return 0;
if(cross(x3,y3,x0,y0,x1,y1)*cross(x3,y3,x,y,x1,y1)<=les) return 0;
return 1;
}
void PointOfIntersection(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
double k1,k2,b1,b2;
if(x1==x2&&x3!=x4)
{
k2=(y3-y4)/(x3-x4);
b2=y3-k2*x3;
x = x1;
y = k2*x1+b2;
}
else if(x1!=x2&&x3==x4)
{
k1=(y2-y1)/(x2-x1);
b1=y1-k1*x1;
x = x3;
y = k1*x3+b1;
}
else if(x1!=x2&&x3!=x4)
{
k1=(y2-y1)/(x2-x1);
b1=y1-k1*x1;
k2=(y3-y4)/(x3-x4);
b2=y3-k2*x3;
x = (b1-b2)/(k2-k1);
y = k1*x+b1;
}
}
int main()
{
freopen("fence4.in","r",stdin);
freopen("fence4.out","w",stdout);
int n,Count;
while(scanf("%d", &n) == 1)
{
memset(res, 0, sizeof(res));
Count = 0;
scanf("%d %d",&ob.x,&ob.y);
for(int i=0; i<n; i++)
scanf("%d %d",&P[i].x,&P[i].y);
for(int i=0; i<n; i++)
{
if(cross(ob.x,ob.y,P[i].x,P[i].y,P[(i+1)%n].x,P[(i+1)%n].y)==0)
continue;
//printf("--------%d-----------\n",i);
bool flag = true;
double ax,ay,bx,by;
ax=P[i].x,ay=P[i].y;
bx=P[(i+1)%n].x,by=P[(i+1)%n].y;
for(int j=(i+1)%n; j!=i; j=(j+1)%n)
{
if(cross(ob.x,ob.y,P[j].x,P[j].y,P[(j+1)%n].x,P[(j+1)%n].y)==0)
continue;
if(intersection(P[j].x,P[j].y,P[(j+1)%n].x,P[(j+1)%n].y,ob.x,ob.y,ax,ay)==1)
{
if(intersection(ob.x,ob.y,bx,by,P[(j+1)%n].x,P[(j+1)%n].y,P[j].x,P[j].y)==1)
{
//if(P[i].x==5&&P[i].y==50)
//printf("j=%d 1\n",j);
flag = false;
break;
}
else if(isInTriangle(ob.x,ob.y,ax,ay,bx,by,P[j].x,P[j].y)==1)
{
//if(P[i].x==5&&P[i].y==50)
//printf("j=%d 2\n",j);
PointOfIntersection(ob.x,ob.y,P[j].x,P[j].y,ax,ay,bx,by);
ax=x;
ay=y;
}
else if(isInTriangle(ob.x,ob.y,ax,ay,bx,by,P[(j+1)%n].x,P[(j+1)%n].y)==1)
{
//if(P[i].x==5&&P[i].y==50)
//printf("j=%d 3\n",j);
PointOfIntersection(ob.x,ob.y,P[(j+1)%n].x,P[(j+1)%n].y,ax,ay,bx,by);
ax=x;
ay=y;
}
}
else if(intersection(P[j].x,P[j].y,P[(j+1)%n].x,P[(j+1)%n].y,ob.x,ob.y,bx,by)==1)
{
if(isInTriangle(ob.x,ob.y,ax,ay,bx,by,P[j].x,P[j].y)==1)
{
//if(P[i].x==5&&P[i].y==50)
//printf("j=%d 4\n",j);
PointOfIntersection(ob.x,ob.y,P[j].x,P[j].y,ax,ay,bx,by);
bx=x;
by=y;
}
else if(isInTriangle(ob.x,ob.y,ax,ay,bx,by,P[(j+1)%n].x,P[(j+1)%n].y)==1)
{
//if(P[i].x==5&&P[i].y==50)
//printf("j=%d 5\n",j);
PointOfIntersection(ob.x,ob.y,P[(j+1)%n].x,P[(j+1)%n].y,ax,ay,bx,by);
bx=x;
by=y;
}
}
}
//printf("%d %d %d %d %lf %lf %lf %lf\n",P[i].x,P[i].y,P[i+1].x,P[i+1].y,ax,ay,bx,by);
if(ax==bx&&ay==by)
{
continue;
}
if(flag==true)
{
Count ++;
res[i]=1;
}
}
printf("%d\n",Count);
for(int i=0; i<n-2; i++)
if(res[i]==1)
{
printf("%d %d %d %d\n",P[i].x,P[i].y,P[i+1].x,P[i+1].y);
}
if(res[n-1]==1) printf("%d %d %d %d\n",P[0].x,P[0].y,P[n-1].x,P[n-1].y);
if(res[n-2]==1) printf("%d %d %d %d\n",P[n-2].x,P[n-2].y,P[n-1].x,P[n-1].y);
}
return 0;
}