【译文】R语言非线性回归入门
【译文】R语言非线性回归入门
作者 Lionel Hertzog
在一簇散点中拟合一条回归线(即线性回归)是数据分析的基本方法之一。有时,线性模型能很好地拟合数据,但在某些(很多)情形下,变量间的关系未必是线性的。这时,一般有三类方法解决这个问题: (1) 通过变换数据使得其关系线性化, (2) 用多项式或者比较复杂的样条来拟合数据, (3) 用非线性函数来拟合数据
从标题你应该已经猜到非线性回归是本文的重点
什么是非线性回归
在非线性回归中,分析师通常采用一个确定的函数形式和相应的参数来拟合数据。最常用的参数估计方法是利用非线性最小二乘法(R中的nls函数)。该方法使用线性函数来逼近非线性函数,并且通过不断迭代这个过程来得到参数的最优解(本段来自维基百科)。非线性回归的良好性质之一是估计出的参数都有清晰的解释(如Michaelis-Menten模型的Vmax是指最大速率),而变换数据后得到的线性模型其参数往往难以解释。
非线性最小二乘拟合
首先,我们以Michaelis-Menten方程为例。
# 生成一些仿真数据
set.seed(20160227)
x <- seq(0, 50, 1)
y <- ((runif(1, 10, 20)*x)/(runif(1, 0, 10)+x)) + rnorm(51, 0, 1)
# 对于一些简单的模型,nls函数可以自动找到合适的参数初值
m <- nls(y ~ a*x/(b+x))
# 计算模型的拟合优度
cor(y, predict(m))
[1] 0.9496598
# 将结果可视化
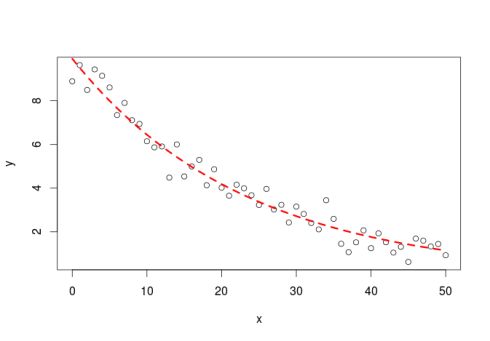
plot(x, y)
lines(x, predict(m), lty = 2, col = "red", lwd = 3)输出的图片如下:
选择适宜的迭代初值
在非线性回归中,找到合适的迭代初值对于整个模型算法的收敛性而言至关重要。假如你设定的参数初值完全脱离了其潜在的取值范围,迭代算法可能不收敛或者返回一些没有意义的参数值。比如返回一个大小为1000的增长率,但其真值却是1.04。寻找合适初值的最好办法是“紧盯着”数据,绘制相应图表并结合你对方程的理解来确定参数的合适初值。
# 生成仿真数据,并且此次对于参数没有先验信息
y <- runif(1, 5, 15)*exp(-runif(1, 0.01, 0.05)*x) + rnorm(51, 0, 0.5)
# 可视化数据并选择一些参数初值
plot(x, y)
# 通过这个散点图确定参数a, b的初值
a_start <- 8 # 参数a是x = 0时y的取值
b_start<- 2*log(2)/a_start # b 是衰减速率
# 拟合模型
m <- nls(y ~ a*exp(-b*x), start = list(a = a_start, b = b_start))
# 计算拟合优度
cor(y, predict(m))
[1] 0.9811831
# 将结果可视化
lines(x, predict(m), col = "red", lty = 2, lwd = 3)输出的图片如下
使用自启动函数
不同的科学研究领域会对同一个模型设定不同的参数形式(即不同的方程),比如研究人口增长的逻辑斯蒂模型,在生态学中一般采用如下形式:
Nt=K∗N0∗ertK+N0∗(ert–1)
等式中的\( N_{t}\)代表时间t时的个体数,\(r\)是个体增长速率,\(K\)是环境承载能力。我们可以将这个等式改写为微分方程的形式:
dNdt=R∗N∗(1−N/K)
library(deSolve)
# 利用逻辑斯蒂模型生成人口增长的仿真数据,并用nls估计参数
log_growth <- function(Time, State, Pars) {
with(as.list(c(State, Pars)), {
dN <- R*N*(1-N/K)
return(list(c(dN)))
})
}
# 逻辑斯蒂增长的参数
pars <- c(R = 0.2, K = 1000)
# 设定初值
N_ini <- c(N = 1)
# 常微分方程的时间阶段(下标t)
times <- seq(0, 50, by = 1)
# 常微分方程
out <- ode(N_ini, times, log_growth, pars)
# 添加一些随机波动
N_obs <- out[, 2]+rnorm(51, 0, 50)
# 个体数值不能小于1
N_obs <- ifelse(N_obs<1, 1, N_obs)
# 画图
plot(times, N_obs)这部分代码只是生成了带有随机误差的仿真数据,接下来的部分会展现估计参数初值的技巧。R语言中有一个估计逻辑斯蒂方程参数的内建函数(SSlogis),但它使用的是如下方程:
Nt=alpha1+exmid−tscale
# 寻找方程的参数
SS <- getInitial(N_obs ~ SSlogis(times, alpha, xmid, scale), data = data.frame(N_obs = N_obs, times = times))我们可使用getInitial函数来对模型参数做一个基于数据的初步估计。然后把该函数的输出作为一个向量化参数传递给自启动函数(SSlogis),同时也将无引号的三个参数名赋值给逻辑斯蒂方程(译者注:即alpha,xmid,scale三个参数)。
然而,由于SSlogis的参数设定有些不同,我们需要对SSlogis的输出值做一些处理,使得其与逻辑斯蒂方程中的形式一致。
# 改变参数形式
K_start <- SS["alpha"]
R_start <- 1/SS["scale"]
N0_start <- SS["alpha"]/(exp(SS["xmid"]/SS["scale"])+1)
# 构建模型的公式
log_formula <- formula(N_obs ~ K*N0*exp(R*times)/(K + N0*(exp(R*times) - 1)))
# 拟合模型
m <- nls(log_formula, start = list(K = K_start, R = R_start, N0 = N0_start))
# 估计参数
summary(m)
Formula: N_obs ~ K * N0 * exp(R * times)/(K + N0 * (exp(R * times) - 1))
Parameters:
Estimate Std. Error t value Pr(>|t|)
K 1.012e+03 3.446e+01 29.366 <2e-16 ***
R 2.010e-01 1.504e-02 13.360 <2e-16 ***
N0 9.600e-01 4.582e-01 2.095 0.0415 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 49.01 on 48 degrees of freedom
Number of iterations to convergence: 1
Achieved convergence tolerance: 1.537e-06
# 计算拟合优度
cor(N_obs,predict(m))
[1] 0.9910316
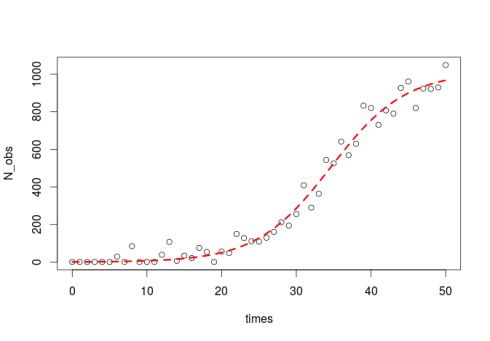
# 结果可视化
lines(times, predict(m), col = "red", lty = 2, lwd = 3)