算术编码JM实现

h.264标准中，CABAC的算术编码部分（9.3.4）只是一个参考，实际编码器中并不一定会按照它来实现，像JM中就有自己的算术编码实现方案。

 

在上篇文章CABAC中有详细的算术编码描述，在了解算术编码原理的基础上，下面分析JM18.6中的算术编码实现。

下图是JM方案编码的一个例子

结合上图的例子分析，JM的方案在下面几部分跟标准有差异

1. 初始化

把$[0,1)$用$[0,2^{26})$来表示，其中有9个bit为$R$，也就是说在初始化时，有

$R \cdot 2^{17} = (R_{MPS}+R_{LPS})\cdot 2^{17} = 2^{26}$

 

void arienco_start_encoding(EncodingEnvironmentPtr eep,
                            unsigned char *code_buffer,
                            int *code_len )
{
  eep->Elow = 0;     // low
  eep->Echunks_outstanding = 0;  //count of  continuous  0xffff
  eep->Ebuffer = 0;  //store the word
  eep->Epbuf = -1;  // to remove redundant chunk ^^  count of bytes to output
  eep->Ebits_to_go = BITS_TO_LOAD + 1; // to swallow first redundant bit  //n = 16 + 1

  eep->Ecodestrm = code_buffer;
  eep->Ecodestrm_len = code_len;

  eep->Erange = HALF;  //0x1fe  510
}

 

2. 重归一化

当输入的是LPS时，会选择$R_{LPS}$作为下次进行符号编码的$R$，但是由于标准规定了$R \in [2^8,2^9)$，因此如果$R_{LPS}$小于$2^8$的话，需要对$R_{LPS}$向左移位。不同大小$R_{LPS}$需要移动不同的位数才能符号区间$[2^8,2^9)$，下面是$R_{LPS}$的范围对应的移位表格

RangeLPS	Renorm Left Shift Bits
[0,7]	6
[8,15]	5
[16,31]	4
[32,63]	3
[64,127]	2
[128,255]	1

$R_{LPS}$进行左移，意味着作为增量的$2^{n}$需要减去相应的位，即

${R^{i}}_{LPS} \times 2^n = ({R^i}_{LPS}<<k) \times 2^{n-k}$

 

void biari_encode_symbol(EncodingEnvironmentPtr eep, int symbol, BiContextTypePtr bi_ct )
{
  ...
  else         //LPS
  {
    unsigned int renorm = renorm_table_32[(rLPS >> 3) & 0x1F];  //get k

    low += range << bl;
    range = (rLPS << renorm);
    bl -= renorm;      // n = n - k

    if (!bi_ct->state)
      bi_ct->MPS ^= 0x01;               // switch MPS if necessary

    bi_ct->state = AC_next_state_LPS_64[bi_ct->state]; // next state

    if (low >= ONE) // output of carry needed
    {
      low -= ONE;
      propagate_carry(eep);
    }

    if( bl > MIN_BITS_TO_GO )  // n > 0 ,no need to save a word yet
    {
      eep->Elow   = low;
      eep->Erange = range;      
      eep->Ebits_to_go = bl;
      return;
    }
  }
  ...
}

 

当输入的是MPS时，会选择$R_{MPS}$作为下次进行符号编码的$R$，但是标准规定了$R\in [2^8,2^9)$，因此如果$R_{MPS}$小于$2^8$的话，需要对$R_{LPS}$左移，不过这里只需要左移一位，因为MPS出现的概率是大于等于0.5的，所以有$2^8 \leqslant 2 \times R_{MPS} < 2^{9}$。最后还需要对n减去1。如果$R_{MPS}$大于或等于$2^8$的话就不需要执行这一步了。

void biari_encode_symbol(EncodingEnvironmentPtr eep, int symbol, BiContextTypePtr bi_ct )
{
  ...
  if ((symbol != 0) == bi_ct->MPS)  //MPS
  {
    bi_ct->state = AC_next_state_MPS_64[bi_ct->state]; // next state

    if( range >= QUARTER ) // no renorm
    {
      eep->Erange = range;
      return;
    }
    else 
    {   
      range<<=1;
      if( --bl > MIN_BITS_TO_GO )  // renorm once, no output //n = n - 1, n>0, no need to save a word yet
      {
        eep->Erange = range;
        eep->Ebits_to_go = bl;
        return;
      }
    }
  }
  ...
}

 

3. 区间起点的计算方法

最终编码输出的是区间起点$L$，由上图可以看出，只有当输入符号位LPS时，L才会增大，有

$L_{i+1} = L_i + {R^i}_{MPS} \cdot 2^n$

当$n$为0时，由于$R$只有9bit，对于一共有26bit的$L$，除了进位之外，后面的计算是不会修改到$L$的高位17个bit的部分了。此时可以保存$L$高位的16bit。

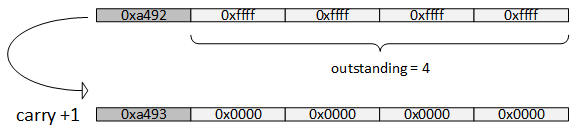
保存下来的16bit数据可能会由于后续计算的进位而+1。需要注意的是，如果保存下来的16bit数据是0xffff，就会由于进位而溢出。解决方法是：每当需要保存的16bit数据为0xffff时，用一个计数器记录0xffff连续出现的次数，一旦碰到进位就把这些0xffff对应的位置置零，并且对它们前面的那个非0xffff的16bit数据+1

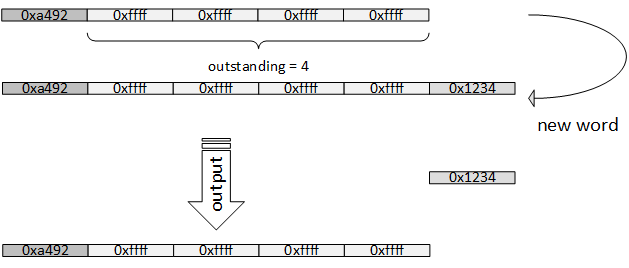
如果在连续出现的0xffff后并没有进位，而是接着保存非0xffff的16bit数据，这时就能将0xffff及其前面的数据一起输出

$L$的26bit数据中，剩下的10bit数据会被再次进行16bit的左移位（n=16），在下次编码符号时作为$L$继续处理。

 

void biari_encode_symbol(EncodingEnvironmentPtr eep, int symbol, BiContextTypePtr bi_ct )
{
  ...
  else         //LPS
  {
    low += range << bl;
    ...

    if (low >= ONE) // output of carry needed
    {
      low -= ONE;
      propagate_carry(eep);  //process carry "+1"
    }
    ...
  }
  ...
  //n = 0, save a word
  //renorm needed
  eep->Elow = (low << BITS_TO_LOAD )& (ONE_M1); //ONE_M1 = 2^26 - 1
  low = (low >> B_BITS) & B_LOAD_MASK; // mask out the 8/16 MSBs for output  //B_BITS=10

  if (low < B_LOAD_MASK) // no carry possible, output now// B_LOAD_MASK=0xFFFF
  {
    put_last_chunk_plus_outstanding(eep, low); //low != 0xFFFF
  }
  else          // low == "FF.."; keep it, may affect future carry
  {
    ++(eep->Echunks_outstanding);  //low == 0xFFFF
  }
}

static forceinline void propagate_carry(EncodingEnvironmentPtr eep)
{
  ++(eep->Ebuffer);   //+1
  while (eep->Echunks_outstanding > 0) 
  { 
    put_one_word(eep, 0);  //set 0xFFFF  0
    --(eep->Echunks_outstanding); 
  }
}

static inline void put_last_chunk_plus_outstanding(EncodingEnvironmentPtr eep, unsigned int l) 
{
  while (eep->Echunks_outstanding > 0)
  {
    put_one_word(eep, 0xFFFF); //it is 0xFFFF, no carry would affect them
    --(eep->Echunks_outstanding);
  }
  put_one_word(eep, l);  //new word
}