<编程珠玑>笔记 (一) 问题-算法-数据结构

1  精确描述问题

   第一章强调的重点在于”精确的描述问题“，这类似程序开发的第一步 -- 需求分析。

1.1  Precise problem statement

1) input: a file containing at most 10⁷ positive intergers (each < 10⁷); any interger occurs twice is an error; no other data is associated with the interger

2) output: a sorted list in increasing order

3) constraints:  at most 1MB available in main memory; ample disk storage; 10s ≤ runtime ＜ several minutes (at most)

1.2  Program design

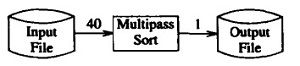
1) mergesort with work files

  read the file once from the input, sort it with the aid of work files that are read and written many times, and then write it once

 

2) 40-pass algorithm

  if we store each number in 4 bytes (32-bit int), we can store 250,000 numbers in 1MB (1 megabytes/4 bytes).

  we use a program that makes 40 passes over the input files. The first pass reads 0 ~ 249,999, and the 40th pass reads 9,750,000 ~ 9,999,999

 

3) read once without intermediate files

  only if we could represent all the integers in the input file in 1MB of main memory (即使利用下文 bitmap 结构，10⁷个整数仍需要1.25MB > 1MB)

 

 1.3  Implementation sketch

  we use bitmap data structure to represent the file by a string of 10⁷ bits in which the ith bit is on only if the interger i is in the file

  E.g. store the set {1, 2, 3, 5, 8, 13} in a string of 20 bits

  0  1  1  1  0  1  0  0  1   0   0   0  0   1   0   0   0  0   0  0 

  1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11,12,13,14,15,16,17,18,19,20

// n is the number of bits in the vector (in this case 10,000,000)
// 1) initialize set to empty
for i = [0, n)
  bit[i] = 0

// 2) insert present elements into the set
for each i in the input file 
  bit[i] = 1

// 3) write sorted output
for i = [0, n)
  if bit[i] == 1
    write i on the output file

View Code

1.4  Principles

  design = right problem + bitmap data structure + multiple-pass algorithm + time-space tradeoff

 

2  三个算法

  在第二章里作者首先提出了三个问题，然后引出各自对应的算法实现。

2.1  Binary search

  Given a sequential file that contain at most 4x10⁹ integers(32-bit) in random order, find a 32-bit integer that is not in the file.

  How would you solve it with ample main memory?  -- bitmap (2³²bits)

  or using several external "scratch" files but only a few hundred bytes of main memory? -- binary search 二分查找

          

  the insight is that we can probe a range by counting the elements above and below its midpoint: either the upper or the lower range has at most half the elements in the total range. Because the total range has a missing element, the smaller half must also have a missing element.

  its only drawback is that the entire table must be known and sorted in advance.

2.2  Rotate -> reverse

  Rotate a one-dimensional vector x of n elements left by i positions. For instance, with n=8 and i=3, the vector abcdefgh is rotated into defghabc.

  Can you rotate the vector in time proportional to n using only a few dozen extra bytes of storage?

  starting with ab, we reverse a to get a^rb, reverse b to get a^rb^r, and then reverse the whole thing to get (a^rb^r)^r, which is exactly ba

reverse(0, i-1)    // cbadefgh
reverse(i, n-1)    // cbahgfed
reverse(0, n-1)    // defghabc

2.3  Signatures

  Given a dictionary of English words, find all sets of anagram. For instance, "pots", "stop" and "tops" are all anagrams of each other.

 

 3  四条原则

   第三章作者给出了四条原则，并重点阐述一种编程观念 “data does indeed structure programs”

1) rework repeated code into arrays

    a long stretch of similar code is often best expressed by the array

2) encapsulate complex structures 封装复杂结构

    define a sophisticated data structure in abstract terms, and express those operations as a class

3) use advanced tools when possible

    Hypertext, name-value pairs, spreadsheets, databases, languages are powerful tools

4) let the data structure the program

     before writing code, thoroughly understand the input, the output and the intermediate data structures

 

4  验证正确性

  在芯片设计(IC)领域有专门的职位叫做芯片验证工程师，他们常用的一种方法叫形式验证(Formal Verification)，具体包括等价性检查，模型检查和定理证明。

  本章所讲的程序验证方法(并非软件测试)，与芯片行业的形式验证非常相似。参考芯片行业，随着分工的细化，软件领域也会出现更多的验证工程师。

4.1  Binary search

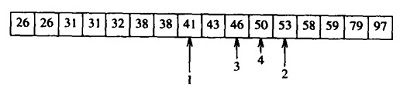
  determine whether the sorted array x[0..n-1] contains the target element t

  mustbe(range): the key idea is that we always know that if t is anywhere in x[0..n-1], then it must be in a certain range of x

1) sketch

/* sketch */
initialize range to 0..n-1
loop
    { invariation: mustbe(range) }
    if range is empty,
        break and report that t is not in the array
    compute m, the middle of the range
    use m as a probe to shrink the range
        if t is found during the shrinking process,
        break and report its position
        

View Code

2) refine

/* refine */
lo = 0; hi = n-1
loop
    { mustbe(lo, hi) }
    if lo > hi
        p = -1; break
    mid = lo/2 + (hi-lo)/2
    case
        x[mid] < t:   lo = mid + 1
        x[mid] == t:  p = m; break
        x[mid] > t:   hi = mid -1
 

View Code

3) program

 1 /* program */
 2 { mustbe(0, n-1) }
 3 lo = 0; hi = n -1
 4 { mustbe(lo,hi) }
 5 loop
 6     { mustbe(lo,hi) }
 7     if lo > hi
 8         { lo > hi && mustbe(lo,hi) }
 9         { t is not in the array }
10             p = -1; break
11         { mustbe(lo,hi) && lo <= hi }
12         m = lo/2 + (hi-lo)/2
13         { mustbe(lo,hi) && lo <= mid <= hi }
14         case 
15             x[mid] < t:
16                     { mustbe(lo,hi) && cantbe(0,mid) }
17                     { mustbe(mid+1,hi) }
18                     lo = mid + 1
19                     { mustbe(lo,hi) }
20             x[mid] == t:
21                     { mustbe(lo,hi) }
22                      p = mid; break
23             x[m] > t:
24                     { mustbe(lo,hi) && cantbe(mid, n-1) }
25                     { mustbe(lo,mid-1) }
26                     hi = mid-1
27                     { mustbe(lo,hi) }
28         { mustbe(lo,hi) }

View Code

4.2  Program verification

1) assertions

    inputs, variables, and output

2) sequential control structures

    "do this statement and then that statement" -- place assertions between them and analyze each step of the program' progress individually

3) selection control structures

    "if", "case": one of many choices is selected -- consider each of the several choices individually

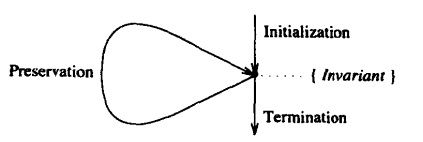
4) iteration control structures

    initialization: invariation is true when the loop is executed the first time

    preservation: invariation is true before and after each iteration of loop

    termination: the desired result is true whenever execution of the loop terminates

   

5) functions

  precondition: the state(inputs, variables) must be true before it is called

  postcondition: what the function will guarantee on termination

int  bsearch( int t, int x[], int n )
/*  precondition: x[0] <= x[1] <= ... <= x[n-1]
     postcondition: 
          result == -1       => t not present in x
          0 <= result < n  => x[result] == t
*/  

View Code

 

5  编程实现

  本章紧接上一章，继续以“二分查找”为例，展示整个程序的实现过程

5.1  coding

/* return (any) position if t is in sorted x[0..n-1] 
    or -1 if t is not present */
int binarysearch(DataType t)
{
    int lo, hi, mid;
    lo = 0;
    hi = n-1;
    
    while(lo < hi)
    {
        mid = lo/2 + (hi-lo)/2;
        if(x[mid] < t)
            lo = mid + 1；
        else if(x[mid] == t)
            return mid;
        else /* x[mid] > t */
            hi = mid -1;
    }
    return -1;    
}

View Code

5.2  testing

5.3  debugging

5.4  timing