贪心算法(4)-最小生成树Prim算法

原文地址  http://www.acmerblog.com/prims-minimum-spanning-tree-mst-5786.html

参考地址   http://www.geeksforgeeks.org/greedy-algorithms-set-5-prims-minimum-spanning-tree-mst-2/

一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的n-1条边。所谓的最小成本，就是n个顶点，用n-1条边把一个连通图连接起来，并且使得权值的和最小。综合以上两个概念，我们可以得出：构造连通网的最小代价生成树，即最小生成树（Minimum Cost Spanning Tree）。找连通图的最小生成树，经典的有两种算法，普里姆算法和克鲁斯卡尔算法，这里介绍普里姆算法。在前面一讲Kruskal最小生成树 中已经介绍了最小生成树的算法。和Kruskal算法类似，Prim算法也是利用贪心算法来解决最小生成树。

最小生成树MST性质：假设N=（V,{E}）是一个连通网，U是顶点集V的一个非空子集。若（u,v）是一条具有最小权值（代价）的边，

其中u∈U，v∈V-U，则必存在一颗包含边（u,v）的最小生成树。

prim算法过程为：

假设N=（V,{E}）是连通图，TE是N上最小生成树中边的集合。算法从U={u0}（u0∈V），TE={}开始，

重复执行下述操作：

在所有u∈U，v∈V-U的边（u，v）∈E中找一条代价最小的边（u0，v0）并入集合TE，同时v0 并入U，直至U=V为止。

此时TE中必有n-1条边，则T=（V，{TE}）为N的最小生成树。

具体描述如下：

1 1） 创建一个集合mstSet记录已经包含在MST中的顶点
2 2）对图中的所有顶点设置一个key值，代表代价，并初始化无穷大。第一个点设置为0，以便总是能第一个取到第一个点
3 3） While( mstSet没有包含所有的顶点 )
4      a) 从mstSet集合中剩下的顶点中，选取一个最小key的顶点u
5      b) 把u加入到mstSet
6      c) 更新所有的和u相连的那些顶点的key值。

如果大家熟悉迪杰斯特拉算法，会发现他们是很相似的。

我以图为例，看看算法过程。

初始的mstSet为空，keys（各个点击的代价）为{0, INF, INF, INF, INF, INF, INF, INF}

找到其中最小的，并加入mstSet，mstSet变为： {0}. 然后更新和0相邻的那些顶点的key值。相邻的顶点为1和7. 更新后为 {0, 4, INF, INF, INF, INF, INF, 8}

下图中绿色表示 mstSet.

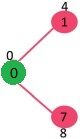
Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.

Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (7 and 1 respectively).

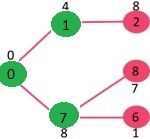
Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.

We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.

Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.

Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (7 and 1 respectively).

Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.

We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.

C++实现如下：

01 #include <stdio.h>
02 #include <limits.h>
03
04 //图中顶点个数
05 #define V 5
06
07 //未在mstSet中的点的集合中，找出最小key的点
08 int minKey(int key[], bool mstSet[])
09 {
10    int min = INT_MAX, min_index;
11
12    for (int v = 0; v < V; v++)
13      if (mstSet[v] == false && key[v] < min)
14          min = key[v], min_index = v;
15
16    return min_index;
17 }
18
19 // 打印MST
20 int printMST(int parent[], int n, int graph[V][V])
21 {
22    printf("Edge   Weight\n");
23    for (int i = 1; i < V; i++)
24       printf("%d - %d    %d \n", parent[i], i, graph[i][parent[i]]);
25 }
26
27 // Prim算法
28 void primMST(int graph[V][V])
29 {
30      int parent[V]; // 保持MST信息
31      int key[V];   // 所有顶点的代价值
32      bool mstSet[V];  //当前包含在MST中点的集合
33
34      // 初始为无穷大
35      for (int i = 0; i < V; i++)
36         key[i] = INT_MAX, mstSet[i] = false;
37
38      key[0] = 0;     //
39      parent[0] = -1; // 第一个作为树的根。
40
41      //  MST 有V的顶点
42      for (int count = 0; count < V-1; count++)
43      {
44         int u = minKey(key, mstSet);
45         // 添加u到 MST Set
46         mstSet[u] = true;
47         //更新和u相连的顶点的代价
48         for (int v = 0; v < V; v++)
49           if (graph[u][v] && mstSet[v] == false && graph[u][v] <  key[v])
50              parent[v]  = u, key[v] = graph[u][v];
51      }
52
53      // 打印生成的MST
54      printMST(parent, V, graph);
55 }
56
57 int main()
58 {
59    /* 创建以下的图
60           2    3
61       (0)--(1)--(2)
62        |   / \   |
63       6| 8/   \5 |7
64        | /     \ |
65       (3)-------(4)
66             9          */
67    int graph[V][V] = {{0, 2, 0, 6, 0},
68                       {2, 0, 3, 8, 5},
69                       {0, 3, 0, 0, 7},
70                       {6, 8, 0, 0, 9},
71                       {0, 5, 7, 9, 0},
72                      };
73
74     // Print the solution
75     primMST(graph);
76
77     return 0;
78 }

输出：

1 Edge   Weight
2 0 - 1    2
3 1 - 2    3
4 0 - 3    6
5 1 - 4    5

时间复杂度：O(V^2).  如果使用 链接表存储的方式并使用堆，复杂度可以为 O(E log V) ，后面会讨论这个算法。

Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.

Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (7 and 1 respectively).

Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.

We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.