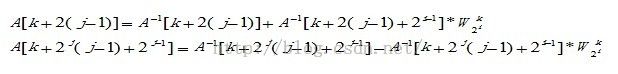[置顶] Python图像处理库PIL中快速傅里叶变换FFT的实现（一）

离散傅里叶变换(discrete Fouriertransform)傅里叶分析方法是信号分析的最基本方法，傅里叶变换是傅里叶分析的核心，通过它把信号从时间域变换到频率域，进而研究信号的频谱结构和变化规律。FFT是一种DFT的高效算法，称为快速傅立叶变换（fastFourier transform）。

在数字图像处理中，FFT的使用非常普遍，是图像处理中最重要的算法之一。在此，我们对FFT算法做一些简单研究，并使用python实现该算法，同时会对图像进行变换分析。

一、FFT算法的原理

FFT算法可分为按时间抽取算法和按频率抽取算法，我们可以从DFT的运算，来FFT的基本原理。

DFT的计算公式如下：

式中

在这两个求和公式中，可以认为x(n)和都是复数，两个复数乘法中，涉及4个乘法和3个加（减）法；再加上累加时的加法，对于每个K值，需要进行4N次实数相乘和（4N-1）次相加。对于N个k值，共需4N*N乘和N（4N-1）次实数相加。如果按照复数来计算的话，对于一个N长的序列，直接计算DFT需要N²次复数乘法以及N（N-1）=N²次复数加法。

由于DFT中的运算量非常大，需要改进DFT算法来减小它的运算量。对于DFT的改进，可以利用DFT中

                          

的周期性和对称性，使整个DFT的计算变成一系列迭代运算，可大幅度提高运算过程和运算量，这就是FFT的基本思想。

FFT基本上可分为两类，时间抽取法和频率抽取法，而一般的时间抽取法和频率抽取法只能处理长度N=2^M的情况，另外还有组合数基四FFT来处理一般长度的FFT。常用的FFT是以2为基数，其长度为N=2^L。当要变换的序列长度不等于2的整数次方时，是为了使用以2为基数的FFT，可以用末位补零的方法，使其长度延长至2的整数次方。

本文将只对FFT的时间抽取法进行介绍并编程实现。

二、FFT的时间抽取法

设N点序列x(n)，

，将x(n)按奇偶分组，公式如下图

改写为：

一个N点DFT分解为两个 N/2点的DFT，

再对N/2阶的DFT做类似运算，在N为2的幂的情况下，最终可以分解成N/2个2阶的DFT运算。比较原先的DFT运算次数和后面的运算次数，原先的N阶DFT需要N2个复数乘法和加法，后面FFT需要Nlog₂N个复数乘法和加法，使用简化蝶形计算更可以减少个复数乘法。

按时间抽取，将8点DFT计算完全分解的图示如下：

使用蝶形计算8点DFT的图示如下：

  

三、FFT时间抽取法的实现

1、 输入数据倒序

从上图可以看出，蝶形运算可以节省内存。整个计算分为三列，每列计算中的蝶形运算仅影响本蝶形运算的结果，我们可以在每次蝶形运算之后将运算结果存入原存储器中，这样仅需要一列长为N的存储器即可。

运算完毕后，序列A(1)、A(2)，…，A(8)，正好对应着最终输出的X(0)，X(1)，X(2)，…，X(7)，可以直接按顺序输出。但蝶形运算的输入x(0)，x(1)，x(2)，…，x(7)却不能按照自然顺序存入存储器，而是按照x(0)，x(4)，x(2)，x(6)，…，x(7)的顺序存入存储单元。这种顺序看起来相当杂乱，然而它也是有规律的。当用二进制表示这个顺序时，它正好是“码位倒置”的顺序。

如果序列A(1)、A(2)，…，A(8)按照数组方式表示A[8]，其与蝶形运算的输入x[8]之间的关系可以表示为：

A[0]= A[000] = x[000] = x[0]

A[1]= A[001] = x[100] = x[4]

A[2]= A[010] = x[010] = x[2]

A[3]= A[011] = x[110] = x[6]

A[4]= A[100] = x[001] = x[1]

A[5]= A[101] = x[101] = x[5]

A[6]= A[110] = x[011] = x[3]

A[7]= A[111] = x[111] = x[7]

2、 蝶形运算

蝶形运算是FFT中最基本的运算单元，在FFT程序设计中要找到蝶形运算地址与第几次迭代，第几组之间的关系。

根据FFT算法的特点，需要设置3个for循环的嵌套循环分别表示迭代、分组和蝶形运算，经过总结得出蝶形运算地址与迭代序号、分组序号间的关系如下：

        上式种A^-1表示前一次迭代运算的结果，i表示迭代序号，j表示分组序号，k表示蝶形运算序号。

对于旋转因子，根据欧拉公式

 

可以得出W_N的变形公式：

W_N=cos(2pi/N)– isin(2pi/N)

 

四、1D FFT的编程实现

使用上述FFT算法，我使用python语言实现了一维FFT变换。具体的code如下：

import math

#define PI 3.1415

#复数类
class complex:
    def __init__(self):
        self.real = 0.0
        self.image = 0.0

#复数乘法
def mul_ee(complex0, complex1):
    complex_ret = complex()
    complex_ret.real = complex0.real * complex1.real - complex0.image * complex1.image
    complex_ret.image = complex0.real * complex1.image + complex0.image * complex1.real
    return complex_ret

#复数加法
def add_ee(complex0, complex1):
    complex_ret = complex()
    complex_ret.real = complex0.real + complex1.real
    complex_ret.image = complex0.image + complex1.image
    return complex_ret

#复数减法
def sub_ee(complex0, complex1):
    complex_ret = complex()
    complex_ret.real = complex0.real - complex1.real
    complex_ret.image = complex0.image - complex1.image
    return complex_ret

#对输入数据进行倒序排列
def forward_input_data(input_data, num):    
    j = num / 2
    for i in range(1, num - 2):        
        if(i < j):
            complex_tmp = input_data[i]
            input_data[i] = input_data[j]
            input_data[j] = complex_tmp
            print "forward x[%d] <==> x[%d]" % (i, j)
        k = num / 2
        while (j >= k):
            j = j - k
            k = k / 2
        j = j + k

#实现1D FFT
def fft_1d(in_data, num):
    PI = 3.1415926
    forward_input_data(in_data, num) #倒序输入数据    

    #计算蝶形级数，也就是迭代次数
    M = 1 #num = 2^m
    tmp = num / 2;
    while (tmp != 1):
        M = M + 1
        tmp = tmp / 2
    print "FFT level：%d" % M

    complex_ret = complex()
    for L in range(1, M + 1):
        B = int(math.pow(2, L -1)) #B为指数函数返回值，为float，需要转换integer
        for J in range(0, B):
            P = math.pow(2, M - L) * J            
            for K in range(J, num, int(math.pow(2, L))):
                print "L:%d B:%d, J:%d, K:%d, P:%f" % (L, B, J, K, P)
                complex_ret.real = math.cos((2 * PI / num) *  P)
                complex_ret.image = -math.sin((2 * PI / num) * P)
                complex_mul = mul_ee(complex_ret, in_data[K + B])
                complex_add = add_ee(in_data[K], complex_mul)
                complex_sub = sub_ee(in_data[K], complex_mul)
                in_data[K] = complex_add
                in_data[K + B] = complex_sub
                print "A[%d] real: %f, image: %f" % (K, in_data[K].real, in_data[K].image)
                print "A[%d] real: %f, image: %f" % (K + B, in_data[K + B].real, in_data[K + B].image)

def test_fft_1d():
    in_data = [2,3,4,5,7,9,10,11] #待测试的8点元素
    #变量data为长度为8、元素为complex类实例的list，用于存储输入数据
    data = [(complex()) for i in range(len(in_data))]
    #将8个测试点转换为complex类的形式，存储在变量data中
    for i in range(len(in_data)):
        data[i].real = in_data[i]
        data[i].image = 0.0
        
    #输出FFT需要处理的数据
    print "The input data:"
    for i in range(len(in_data)):
        print "x[%d] real: %f, image: %f" % (i, data[i].real, data[i].image)
         
    fft_1d(data, 8)

    #输出经过FFT处理后的结果
    print "The output data:"
    for i in range(len(in_data)):
        print "X[%d] real: %f, image: %f" % (i, data[i].real, data[i].image)
   
#test the 1d fft
test_fft_1d()


    

        

运行该程序后，其输出如下：

The input data:
x[0] real: 2.000000, image: 0.000000
x[1] real: 3.000000, image: 0.000000
x[2] real: 4.000000, image: 0.000000
x[3] real: 5.000000, image: 0.000000
x[4] real: 7.000000, image: 0.000000
x[5] real: 9.000000, image: 0.000000
x[6] real: 10.000000, image: 0.000000
x[7] real: 11.000000, image: 0.000000
forward x[1] <==> x[4]
forward x[3] <==> x[6]
FFT level：3
L:1 B:1, J:0, K:0, P:0.000000
A[0] real: 9.000000, image: 0.000000
A[1] real: -5.000000, image: 0.000000
L:1 B:1, J:0, K:2, P:0.000000
A[2] real: 14.000000, image: 0.000000
A[3] real: -6.000000, image: 0.000000
L:1 B:1, J:0, K:4, P:0.000000
A[4] real: 12.000000, image: 0.000000
A[5] real: -6.000000, image: 0.000000
L:1 B:1, J:0, K:6, P:0.000000
A[6] real: 16.000000, image: 0.000000
A[7] real: -6.000000, image: 0.000000
L:2 B:2, J:0, K:0, P:0.000000
A[0] real: 23.000000, image: 0.000000
A[2] real: -5.000000, image: 0.000000
L:2 B:2, J:0, K:4, P:0.000000
A[4] real: 28.000000, image: 0.000000
A[6] real: -4.000000, image: 0.000000
L:2 B:2, J:1, K:1, P:2.000000
A[1] real: -5.000000, image: 6.000000
A[3] real: -5.000000, image: -6.000000
L:2 B:2, J:1, K:5, P:2.000000
A[5] real: -6.000000, image: 6.000000
A[7] real: -6.000000, image: -6.000000
L:3 B:4, J:0, K:0, P:0.000000
A[0] real: 51.000000, image: 0.000000
A[4] real: -5.000000, image: 0.000000
L:3 B:4, J:1, K:1, P:1.000000
A[1] real: -5.000000, image: 14.485281
A[5] real: -5.000000, image: -2.485281
L:3 B:4, J:2, K:2, P:2.000000
A[2] real: -5.000000, image: 4.000000
A[6] real: -5.000000, image: -4.000000
L:3 B:4, J:3, K:3, P:3.000000
A[3] real: -5.000000, image: 2.485281
A[7] real: -4.999999, image: -14.485281
The output data:
X[0] real: 51.000000, image: 0.000000
X[1] real: -5.000000, image: 14.485281
X[2] real: -5.000000, image: 4.000000
X[3] real: -5.000000, image: 2.485281
X[4] real: -5.000000, image: 0.000000
X[5] real: -5.000000, image: -2.485281
X[6] real: -5.000000, image: -4.000000
X[7] real: -4.999999, image: -14.485281

经过确认，输出X[]是符合预期的。

（未完待续）