碰撞回避算法(一) Velocity Obstacle

碰撞回避是机器人导航，游戏AI等领域的基础课题。几十年来，有许多算法被提出。注意这里主要指的是局部的碰撞回避算法，虽然和全局的路径规划算法（A*算法等）有千丝万缕的联系，但是还是有所不同的(局部的碰撞回避算法主要关注的是即将发生的碰撞，而路径规划主要关注的是事先确定出到达目的地的最佳路径，这两种算法通常需要配合使用)。近年，一种基于Velocity Obstacle [1]的ORCA算法因为其实时性，在许多3A级游戏中被广泛采用。这里我们就介绍一下这种高性能的算法。

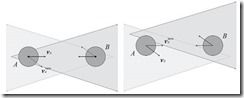
首先考虑一下最基本的情形，有两个圆形的机器人A和B在同一个平面上以一定的速度移动着，那么我们要如何判断它们是否会发生碰撞？

一种比较直观的方法就是，算出A对于B的相对速度，然后看看相对速度的方向是否在宽度为两者半径之和的扇区内。如果在，那么这两个机器人在未来某个时间点必然会发生碰撞。

反过来说，只要相对速度在这个扇区范围之外，那么就不会发生碰撞。如果要获得对于绝对速度Va的“碰撞范围”，只要将相对速度的“碰撞范围”根据Vb进行平移即可。而这个“碰撞范围”就是A对于B的Velocity Obstacle。正式的定义如下：

其中

那么如果有复数个机器人，对于B来说，就不止有一个Velocity Obstacle。此时，只要选择在所有的Velocity Obstacle的集合之外的速度就能够保证不会发生碰撞。

该方法的好处在于直观以及计算简便，只需要构建出每个Velocity Obstacle的两条边，便可以直接选择速度，不像许多其他的算法需要计算距离。当然，还有一些具体的问题，如应该选择哪一块区域，或者没有可选择区域时应该如何选择等，这里我就不多加介绍了，有兴趣的同学可以自行查看后面所列出的参考文献。

这很棒，没错。但是，当其他的机器人也采取同样的回避措施的时候，会发生什么？

可以想象以下的情形，

两个机器人A和B都向着各自的目标迎面而行，他们的速度都处于各自的Velocity Obstacle中，也就是说接下来会发生碰撞，A与B都会选择Velocity Obstacle之外的速度进行回避。一段时间之后，他们的速度都将处于各自的Velocity Obstacle之外。但是，为了尽快的到达目的地，他们又会重新选择原来的速度，重复上述动作。最终他们的运动轨迹会变成下图所示，这种抖动不仅不自然，也会影响各自的速度。

这个问题的根源在于Velocity Obstacle算法假定机器人B以外的机器人都不会采取回避行动，而只是以固定速度朝着各自的目的地前进。也就是说，回避的责任全部交给了B。而当其他机器人也采取同样的回避策略时，便会出现上述的问题。为了解决这个问题，在2007年开始的之后几年间，University of North Carolina at Chapel Hill的研究小组Gamma提出了Reciprocal Velocity Obstacle以及它的改良算法Optimal Reciprocal Collision Avoidance，并获得了非常好的回避性能。这些算法具体是怎样的，让我们留待下回分解。

参考文献

[1] P. Fiorini and Z. Shiller, “Motion planning in dynamic environments using velocity obstacles,” Int. J. Robot. Res., vol. 17, no. 7, pp. 760–772, Jul. 1998.

P.S. 该文章使用Live Wirter发布，似乎图片被自动缩小了，看不清的话可以点击查看原图