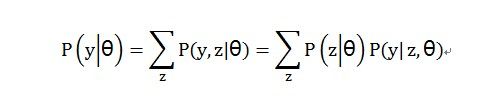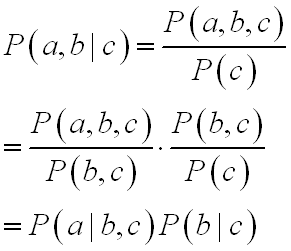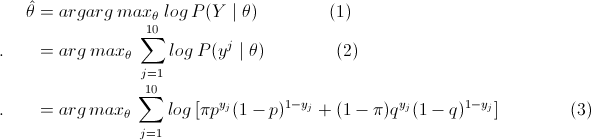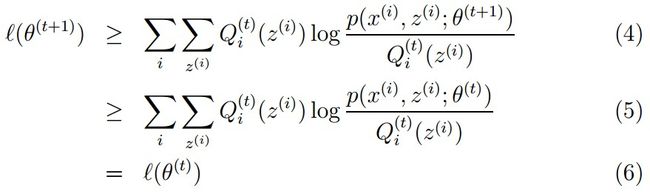机器学习:EM算法
1. 定义
EM(Expectation Maximization), 期望极大算法,是一种从不完全数据或有数据丢失的数据集(存在隐含变量)中求解概率模型参数的最大似然估计方法。用户含有隐变量的的概率模型参数的极大似然估计,或称极大后验概率估计法。
EM应用:高斯混合模型、隐马尔可夫模型的模型学习。
EM推广:GEM算法。
2. 原理
《统计学习方法》一书中给出一个案例“三硬币模型”:EM算法学习(Expectation Maximization Algorithm)
有3个硬币,分布为A、B、C,硬币正面的概率是pai,p,q。投币实验如下,先投A,如果A是正面,即A=1,那么选择投B;A=0,投C。最后,如果B或者C是正面,那么y=1;是反面,那么y=0;投n次,n=0,结果序列是 :1,1,0,1,0,0,1,0,1,1
解:设随机变量y是观测变量,则投掷一次的概率模型为
![]()
这里涉及一个条件概率: 多变量条件概率等价式推导
Θ是向量pai,p,q。y是观察到的硬币最终的正反面。Z是硬币A的投掷结果,是没有未观察到的。
有n次观测数据Y,那么观测数据Y的似然函数为
这里将概率模型公式和似然函数代入(1)式中,可以很轻松地推出 (1)=> (2) => (3),然后选取θ(π,p,q),使得(3)式值最大,即最大似然。然后,我们会发现因为(3)中右边多项式+符号的存在,使得(3)直接求偏导等于0或者用梯度下降法都很难求得θ值。
这部分的难点是因为(3)多项式中+符号的存在,而这是因为这个三硬币模型中,我们无法得知最后得结果是硬币B还是硬币C抛出的这个隐藏参数。那么我们把这个latent 随机变量加入到 log-likelihood 函数中,得

略看一下,好像很复杂,其实很简单,请容我慢慢道来。首先是公式(4),这里将zi做为隐藏变量,当z1为结果由硬币B抛出,z2为结果由硬币C抛出,不难发现
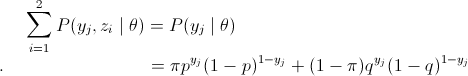
注:一下Q中有些许漏了下标j,但不影响理解
接下来公式说明(4)=> (5)(其中(5)中Q(z)表示的是关于z的某种分布,![]() ),很直接,在P的分子分母同乘以Q(zi)。最后是(5)=>(6),到了这里终于用到了第二节介绍的Jensen不等式,数学好的人可以很快发现,
),很直接,在P的分子分母同乘以Q(zi)。最后是(5)=>(6),到了这里终于用到了第二节介绍的Jensen不等式,数学好的人可以很快发现,
 就是
就是![]() 的期望值
的期望值
且log是上凸函数,所以就可以利用Jensen不等式得出这个结论。因为我们要让log似然函数l(θ)最大,那么这里就要使等号成立。根据Jensen不等式可得,要使等号成立,则要使![]() 成立。
成立。
再因为![]() ,所以得
,所以得![]() ,c为常数,那么
,c为常数,那么

这里可以发现
3. EM的算法流程
初始化分布参数θ;
重复以下步骤直到收敛:
E步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:
M步骤:将似然函数最大化以获得新的参数值:
这个不断的迭代,就可以得到使似然函数L(θ)最大化的参数θ了。那就得回答刚才的第二个问题了,它会收敛吗?
感性的说,因为下界不断提高,所以极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。理性分析的话,就会得到下面的东西: