图
图G只不过是对于个体集合上二元关系的一种编码方式
无向图e={u,v},u和v是e的端点
有向图,比如e=(u,v),u,v是一对有序对
图的具象表示:
运输网络:航班机场。高速公路站点
通信网络:计算机的通信网络连接。支配整个因特网路由标准的BGP协定下交换数据的一个协定,就用一条边连接u和v(和前一个网相比后一个网是"虚拟"的,因为这个链接表示了在一个物理链接上附加的形式协定)。无线网的有向图,比如u到v,u是一个比v强很多的发射机,v只能接收信息
信息网络:万维网的超链接
社会网络:结点表示各种个体,连线表示结点之间的某些关系
依赖网络:某课程的先修课程,食物链(网)
路径和连通性:
对无向图
简单图:一条路径的所有结点都是相互不同的
圈:存在相同结点的路径
对所有图
无向图的连通性:对于每对结点u,v,都存在一条路径
有向图连通性复杂些而同理
有向图的强连通性:对于每对结点,同时存在u到v和v到u的路径
树
一个无向图是连通的,且不包含一个圈,删除任意一条边都会不连通
每棵n个结点的树有n-1条边
相容定理:(2推1)
G是连通的
G不包含一个圈
G有n-1条边
图的连通性和图的遍历:
图的连通性
问题:图G(V,E)中,任意a,d节点是否存在一个路径,即连通(又可称之为 迷宫求解问题)
算法:
宽度优先搜索(BFS) -队列
构造层L1,L2,L3......
假设从a开始,到Lj层,Lj层所有点到a的‘距离’相同
可由此构造宽度优先搜索树
(2与3也可连通,用虚线)
:若两点分别属于Li与Lj,且两点之间有1线连接,则i与j至多相差1
不仅能解决路径连通问题,而且是最短路径连通
本质:
探查一个连通分支:
运行BFS算法,建立从s开始能到达点的集合R,判断d是否属于R即可
(R(s)=R(a)=R())
R将由那些有一条路径从s通向它的结点组成
初始 R= {s}
While 存在一条边(u,v),其中u属于R,v不属于R
将v加到R中
Endwhile
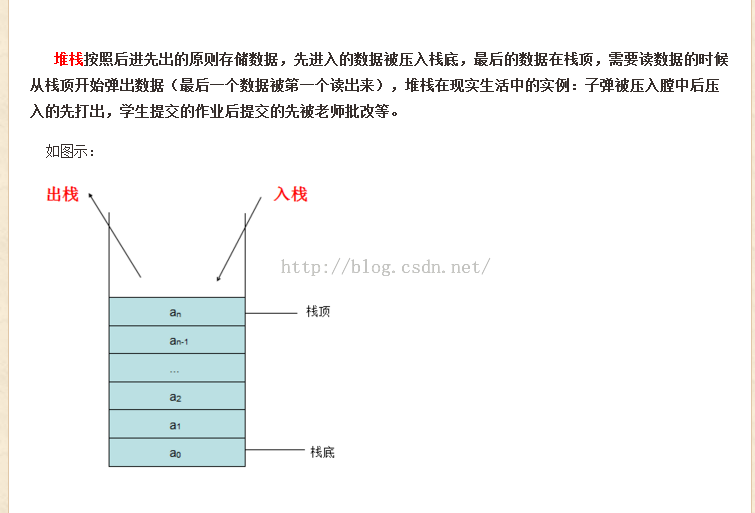
深度优先搜索(DFS)- 栈
DFS(a): 从a开始选择 未标explored的邻接点一直下去 if u找不到 未标explored的邻接点 then 将 u加入R集 if 设u的上一个经过点为v 递归调用 DFS(v) Endif定理:对(无向)图中任意两个结点s与t,它们的连通分支要么相等,要么不相交
证明:因if q属于R(a),则当搜索到q结点时,R(q)=R(a)
则 if p属于R(s)交R(t),R(s)=R(p)=R(t)
图的表示
邻接矩阵:v,w存在一条边 aij = 1
v,w不存在一条边 aij = 0
存储复杂度o(n^2)
邻接表:
G=(V,E),n=l V l(点的个数) ,m= l E l(边的个数)
建立一个长为n的指针数组来建立在Adj中的表(Adj[v]是包含邻接到v的所有结点的记录)
易知 l Adj l=2m
则存储复杂度 o(n+2m)=o(n+m)
m<=n^2
当图为稀疏图时,邻接表显然更好用
队列:
<span style="font-size:14px;"><strong>BFS</strong>(s): 置Discovered[s]=ture 且对所有其它的v,置Discovered[v]=false 初始化L[0]只包含s一个元素 置当前BFS树 T不是空集 While L[i] 不空 初始化一个空表L[i+1] For 每个结点u属于L[i] 考虑每条关联到u的边(u,v) if Discovered[v]=false then Discovered[v]=true 把边(u,v)加在树T上 把v加到表L[i]上 Endif Endfor i++ Endwhile</span>
如果上述算法中,图是由邻接表给出,BFS的时间复杂度 o(m+n)
栈:
<strong>DFS(s)</strong>: 初始化S为具有1个元素s的栈 While S 非空! 从S中取一个结点u(栈顶) if Explored[u]=false then Explored[u]=ture For 每条与u关联的边(u,v) 把所有v 加到栈S中 Endfor Endif Endwhile数据提取o(m+n),加入栈结点数o(m),所以算法复杂度o(m+n)
找出所有连通分支的集合
与DFS和BFS等价,o(m+n)
二分性测试:BFS
二部图:点与相邻点着色不同
定理:如果一个图是二部图,那么它不可能包含一个奇圈
设计算法:
在BFS的基础上引入Color数组即可
i=奇数,Color[i]=红
Color[i+1]=蓝
恰成立定理:
i)偶数层都是红色,奇数层都是蓝色是二部图
ii)同一层有结点相交不可能是二部图
有向图中的连通性:
图搜索算法:
i) 从s开始,s能到达的t结点,尽管t也许不能回到s,BFS
ii)定义一个新的有向图G^rev,从s开始,记录能到达s的t结点
强连通性:
命题:
若u和v是相互可达,v和w是相互可达,那么u和w相互可达
定理:
对有向图的任意两个结点s和t,它们的强连通分支要么相等,要么不相交
有向无圈图与拓扑排序:
无向无圈图:构成数
有向无圈图:DAG(例:表示优先关系或依赖性的描述,课程预修要求,计算作业的流水线,时间优先的任务集)
拓扑排序:v1,v2,v3..vi..vj...i小于j,且结点都是向前指,表示到达vj时,要求比他优先的任务都做完了
定理:如果G有一个拓扑排序,那么G是一个DAG(易证)
命题:在每个DAG中,存在一个没有输入边的结点(易证)
定理:如果G是一个DAG,那么G有一个拓扑排序
找到一个没有输入边的结点v并将其排到第一
从G中删除v
递归计算G-{v}的拓扑序列并把这个序接在v的后面
(G-{v}不可能构成之前就不存在的圈)
我们找到一个没有进入边的结点v并且删除,需要o(n),总的n次迭代,o(n^2)
改进o(m+n)
维护:(如果一个结点没被算法删除,那么就是活跃的)
a) 对每个结点w,从活跃点进入w的边数;
b)从其它活跃结点没有边进入的G中所有活跃结点集合S
进行a,b初始化 <strong>o(n+m)</strong> 从S中选出结点v并删除 ; <strong> o(n)</strong> 检查v有边通向的所有结点w; <strong>o(1)</strong> 活跃结点w的边数-1,w=0则加入S; <strong> o(n)</strong> 继续迭代
问题
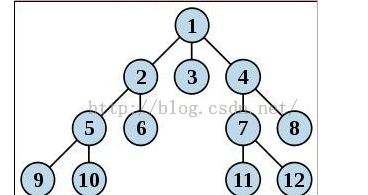
1:给定如上有向无圈图,它有多少种拓扑排序?
<strong>从邻接表中搜索 检索出无输入结点a 以a为起始点然后构造树层Lj 最后以L1 L2 L3....形式输出 (同一层排列随机,n!)</strong>
2:给出一个算法来探测一个给定的无向图是否包含一个圈,如果这个图包含圈,那么你的算法就该输出它(1个圈即可)
找到一个没有输入边的结点v <strong>o(n)</strong>
从G中删除v
迭代
if lGl>1
{ 则剩下的结点会构成圈(>=1)
调用DFS直至碰到2次相同的结点 <strong>o(n+m)</strong>
输出这段路径之间的结点 }
if lGl=1
则不存在一个圈
从m个判断中构造邻接表 初始化所有结点=0 <strong>o(n)</strong> 从邻接表中任选一个结点a 构造2个数组color[a]和color[~a] BFS <strong>o(m+n)</strong> 与母结点相同的子结点与母节点同数组,反之不同,又若归为color[a]数组,结点+1,反之-1 如果在2数组中存在结点=0 则不自恰 反之自恰
4:一颗二叉树是一棵每个结点至多有两个孩子的根树,用归纳法证明叶子数恰好比具有2个孩子的结点树多1
层数N=1时,叶子=1,结点=0,满足
层数N=2时,i)叶子=1,结点=0,ii)叶子=2,结点=1,满足
若层数N=i时,结点=叶子(i)-1
层数N=i+1时,归化为i-1个层数为2的'小'树,若i)情况有p种,ii)有i-p种
那么结点=i-1+i-p
叶子=p+2(i-p)=结点+1
成立
5:G在u点的深度优先搜索树包含所有结点,那么也是u的一棵宽度优先搜索树
因为
D(T)<=B(T)<=T
又D(T)=T
所以成立