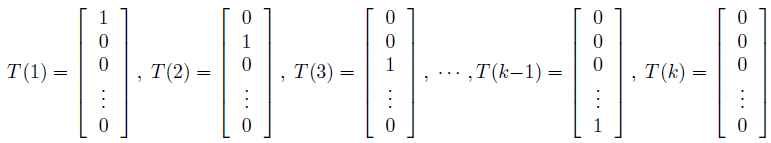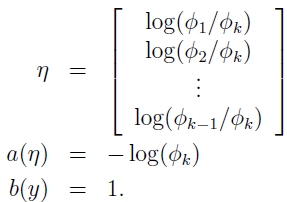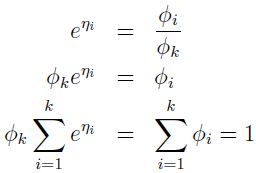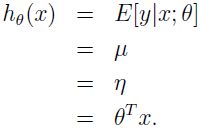机器学习笔记—指数分布簇和广义线性模型
![]()
![]()
在分类例子中:
可以看出,μ 和 Φ 是作为 x 和 θ 的函数来定义的。
在本文会看到,这两个模型其实都只是一个广大模型家族的特例,广义线性模型。我们也将演示广义线性模型家族的其它模型如何推导,并如何应用到分类和回归问题中的。
在讨论广义线性模型之前,我们先来定义指数分布簇。当一个分布能写成以下形式时,我们就说它属于指数分布簇。
η 是分布的自然参数;
T(y) 是充分统计量,通常 T(y)=y;
a(η) 被称为 log partition function;
e-a(η) 起着归一化常数的作用,保证分布 p(y;η) 积分从 y 到 1。
当参数 a、b、T 固定后,就定义了一个以 η 为参数的分布簇。改变 η,就得到这个分布簇的一个不同分布。
伯努利和高斯分布其实也是指数簇分布的特例。
伯努利分布均值为 Φ,y 只有 0 和 1 两个值。
![]()
改变 Φ,就得到不同均值的伯努利分布。
通过选择 T、a 和 b,指数分布簇通用公式能变成伯努利分布。先来把伯努利分布变成指数分布簇的形式。
跟指数分布簇公式相比对:
可得:
其中 η=log(Φ/(1-Φ)),那么 Φ=1/(1+e-η),这就是熟悉的 simoid 函数,这就是说我们把 Logistic 回归当做广义线性回归来推导的话也能推出 sigmoid 函数。
接下来看高斯分布,记得在线性回归的推导时,方差 σ2 的值对我们最后的 θ 和 hθ(x) 值没有任何影响。所以,我们给 σ2 随便选个值就行,方便起见,令 σ2=1,得:
其中:
可见,高斯也属于指数分布簇。
还有其它的很多分布也属于指数分布簇,如多项式分布、泊松分布、伽马分布、指数分布、贝塔分布和 Dirichlet 分布等。
下面讲广义线性模型。
假定你想要建一个模型来估计在某个时刻到商店的顾客个数,或者估计你的网页的浏览量,基于一些特征,如促销活动、最近的广告、天气、星期几等。我们知道泊松分布通常是这种好模型。怎么才能针对我们的问题建模呢?泊松分布是个指数分布簇,所以我们可以使用广义线性模型。
考虑下分类和回归问题,把随机变量 y 作为 x 的函数,来预测 y 值。在这个问题上,我们要推导广义线性模型,关于 y 对 x 的条件分布,我们将做一下三种假设:
1、y|x;θ~ExponetialFamily(η)。即给定 x 和 θ,y 符合以 η 为参数的指数簇分布。
2、给定 x,目标是要预测 T(y),在大部分例子中,我们有 T(y)=y,这意味着我们学习到的 h(x) 满足 h(x)=E[y|x]。(Logistic 回归和线性回归中的 hθ(x) 是满足这个假设的,如 Logistic 回归中,hθ(x)=p(y=1|x;θ)=1·p(y=1|x;θ)+0·p(y=0|x;θ)=E[y|x;θ])
3、自然参数 η 和输入 x 成线性关系:η=θTx。
这三个假设使我们可以导出一个非常优雅的学习算法类,称作 GLMs,有很多属性如易学习。而且,模型对于建模关于 y 的不同分布是很有效的,如 Logistic 回归和最小二乘模型就可以由 GLMs 导出。
先来演示 GLM 簇模型的一个特例,最小二乘。目标变量 y 是连续的,我们把 y 对于 x 的条件分布建模为高斯分布 Ν(μ,σ2),这里 μ 依赖于 x。所以,我们让这里的 ExponetialFamily(η) 分布为高斯分布,高斯作为指数簇分布的形式中,μ=η。有
第一个等式符合上面的假设 2,第二个等式符合事实 y|x;θ~Ν(μ,σ2),所以期望值是 μ,第三个等式符合假设 1(我们早先的求导显示高斯分布作为指数分布簇 μ=η),最后一个等式符合假设 3。
再来看 Logistic 回归,y€{0,1},,y 是二值的,所以看起来选择伯努利分布来建模 y 对于 x 的条件分布是很自然的。伯努利分布属于指数分布簇,Φ=1/(1+e-η)。y|x;θ~Bernoulli(Φ),所以 E[y|x;θ]=Φ。
假设函数 hθ(x)=1/(1+e-θTx) ,之前我们想知道为什么使用 Logistic 函数 1/(1+e-z),这就是答案:一旦我们假定基于 x 的 y 的条件分布是伯努利,那么它就是GLMs 和指数分布簇的定义的结果。
多介绍一些术语,函数 g,作为自然参数的函数给定的分布均值,被称为正则响应函数(canonical response function),它的反函数 g 是正则关联函数(canonical link function)。所以,正则响应函数对于高斯家族只是 identity 函数,对于伯努利是 logistic 函数。
我们证实了 Logistic 回归和线性回归都属于广义线性模型,那么这个广义线性模型 GLM 有什么用呢?我们能通过 GLM 解决更多的问题吗?如何解决?下面就来举个例子。
考虑一个分类问题,响应变量 y 能取 k 个值,所以 y€{1,2,...,k}。例如,我们不仅想把邮件分为垃圾邮件和非垃圾邮件,可建成二分类问题,还想把邮件分为垃圾邮件、私人邮件和工作邮件。响应变量依然是离散的,但能取多个值。我们将把它建模成多项式分布。
为对这类多项式数据建模,我们先来推导 GLM。我们先把多项式表示为一个指数分布簇。
k 个参数 Φ1,Φ2,...,Φk 指定了每个输出的概率。事实上,这些参数是有冗余的,因为 Φ1+Φ2+...+Φk=1,所以,我们可以参数化多项式为 k-1 个参数 Φ1,Φ2,...,Φk-1,其中 Φi=p(y=i;Φ),p(y=k;Φ)=1-(Φ1+Φ2+...+Φk-1)。为表示方便,我们也可以让 Φk=1-(Φ1+Φ2+...+Φk-1),但应知道这不是个参数。
将多项式表示成一个指数分布簇,我们定义 T(y)€Rk-1 如下:
跟之前的例子不一样,这里不是 T(y)=y, T(y)现在是一个 k-1 维的向量,而不是一个实数。我们用 (T(y))i 表示向量 T(y) 的第 i 个元素。
这里介绍一个有用的符号。指示函数 1{·},1{True}=1,1{False}=0。例如,1{2=3}=0,1{3=5-2}=1。所以,我们可以把 T(y) 和 y 的关系写成 (T(y))i=1{y=i}},更进一步,E[(T(y))i]=p(y=i)=Φi。
现在我们将演示,多项式是指数分布簇:
其中:
这就完成了多项式作为指数分布簇的形式化。
关于 η 可以跟伯努利分布 η=log(Φ/(1-Φ)) 和高斯分布 η=µ 作个对比。
连接函数为:
方便起见,定义 ηk=log(Φk/Φk)=0。 为转化连接函数,导出响应函数,我们有
这表示 Φk=1/(eη1+eη2+...+eηk),响应函数:
这个从 η 映射到 Φ 的函数称作 softmax 函数。
继续完善我们的模型,使用 GLM 的假设 3,ηi 跟 x 的线性相关。所以,ηi=θiTx(i=1,...,k-1),其中 θ1,...θk-1 €Rk+1 是我们模型的参数。方便表示起见,我们也定义 θk=0,所以 ηk=θkTx=0。所以,我们的模型假定给定 x 后 y 的条件分布为:
这种模型,应用到分类问题,y€{1,...,k},被称为 softmax 回归。这是 Logistic 回归的归纳。
我们的假设将有:
换句话说,我们的假设将输出 p(y=i|x;θ) 的概率估计,对于每个 i=1,...,k。
上面 hθ(x) 的公式可跟线性回归和 Logistic 回归的 hθ(x) 作对比:
最后讨论寻找最佳参数。跟最小二乘和 Logistic 回归的原始求导类似,如果我们有 m 个例子的训练集 {(x(i),y(i));i=1,...,m},想要学习这个模型的参数 θi,log 似然函数为:
现在我们可以通过最大化 l(θ) 的 θ 来最大化似然估计,使用梯度下降或者牛顿方法。
关于 l(θ) 依然可以跟线性回归和 Logistic 回归做对比。
参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes1.pdf
2、http://blog.csdn.net/stdcoutzyx/article/details/9207047