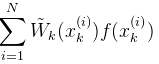Particle Filter Tutorial 粒子滤波：从推导到应用（四）
六、Sampling Importance Resampling Filter (SIR)
SIR滤波器很容易由前面的基本粒子滤波推导出来，只要对粒子的重要性概率密度函数做出特定的选择即可。在SIR中，选取：
p( x(k)|x(k-1) )这是先验概率，在第一章贝叶斯滤波预测部分已经说过怎么用状态方程来得到它。将这个式子代入到第二章SIS推导出的权重公式中：
得到：
(1)式
由之前的重采样我们知道，实际上每次重采样以后，有。
所以(1)式可以进一步简化成：
这里又出来一个概率采样
，实际怎么得到这个概率，程序里面又怎么去采样呢？
先搞清这个概率的含义，它表示在状态x出现的条件下，测量y出现的概率。在机器人定位里面就是，在机器人处于位姿x时，此时传感器数据y出现的概率。更简单的例子是，我要找到一个年龄是14岁的男孩（状态x），身高为170（测量y）的概率。要知道y出现的概率，需要知道此时y的分布。这里以第一篇文章的状态方程为例，由系统状态方程可知，测量是在真实值附近添加了一个高斯噪声。因此，y的分布就是以真实测量值为均值，以噪声方差为方差的一个高斯分布。因此，权重的采样过程就是：当粒子处于x状态时，能够得到该粒子的测量y。要知道这个测量y出现的概率，就只要把它放到以真实值为均值，噪声方差为方差的高斯分布里去计算就行了：
到这里，就可以看成SIR只和系统状态方程有关了，不用自己另外去设计概率密度函数，所以在很多程序中都是用的这种方法。
下面以伪代码的形式给出SIR滤波器：
----------------------SIR Particle Filter pseudo code-----------------------------------
- FOR i = 1:N
(1)采样粒子：
(2)计算粒子的权重：
- END FOR
- 计算粒子权重和，t=sum(w)
- 对每个粒子，用上面的权重和进行归一化,w = w/t
- 粒子有了，每个粒子权重有了，进行状态估计
- 重采样
在上面算法中，每进行一次，都必须重采样一次，这是由于权重的计算方式决定的。
分析上面算法中的采样，发现它并没有加入测量y(k)。只是凭先验知识p( x(k)|x(k-1) )进行的采样，而不是用的修正了的后验概率。所以这种算法存在效率不高和对奇异点(outliers)敏感的问题。但不管怎样，SIR确实简单易用。
七、粒子滤波的应用
在这里主要以第一章的状态方程作为例子进行演示。
在这个存在过程噪声和量测噪声的系统中，估计状态x(k)。
%% SIR粒子滤波的应用，算法流程参见博客http://blog.csdn.net/heyijia0327/article/details/40899819
clear all
close all
clc
%% initialize the variables
x = 0.1; % initial actual state
x_N = 1; % 系统过程噪声的协方差 (由于是一维的，这里就是方差)
x_R = 1; % 测量的协方差
T = 75; % 共进行75次
N = 100; % 粒子数，越大效果越好，计算量也越大
%initilize our initial, prior particle distribution as a gaussian around
%the true initial value
V = 2; %初始分布的方差
x_P = []; % 粒子
% 用一个高斯分布随机的产生初始的粒子
for i = 1:N
x_P(i) = x + sqrt(V) * randn;
end
z_out = [x^2 / 20 + sqrt(x_R) * randn]; %实际测量值
x_out = [x]; %the actual output vector for measurement values.
x_est = [x]; % time by time output of the particle filters estimate
x_est_out = [x_est]; % the vector of particle filter estimates.
for t = 1:T
x = 0.5*x + 25*x/(1 + x^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
z = x^2/20 + sqrt(x_R)*randn;
for i = 1:N
%从先验p(x(k)|x(k-1))中采样
x_P_update(i) = 0.5*x_P(i) + 25*x_P(i)/(1 + x_P(i)^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
%计算采样粒子的值，为后面根据似然去计算权重做铺垫
z_update(i) = x_P_update(i)^2/20;
%对每个粒子计算其权重，这里假设量测噪声是高斯分布。所以 w = p(y|x)对应下面的计算公式
P_w(i) = (1/sqrt(2*pi*x_R)) * exp(-(z - z_update(i))^2/(2*x_R));
end
% 归一化.
P_w = P_w./sum(P_w);
%% Resampling这里没有用博客里之前说的histc函数，不过目的和效果是一样的
for i = 1 : N
x_P(i) = x_P_update(find(rand <= cumsum(P_w),1)); % 粒子权重大的将多得到后代
end % find( ,1) 返回第一个 符合前面条件的数的 下标
%状态估计，重采样以后，每个粒子的权重都变成了1/N
x_est = mean(x_P);
% Save data in arrays for later plotting
x_out = [x_out x];
z_out = [z_out z];
x_est_out = [x_est_out x_est];
end
t = 0:T;
figure(1);
clf
plot(t, x_out, '.-b', t, x_est_out, '-.r','linewidth',3);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('flight position');
legend('True flight position', 'Particle filter estimate');
滤波后的结果如下：
这是粒子滤波的一个应用，还有一个目标跟踪(matlab)，机器人定位(python)的例子，我一并放入压缩文件，供大家下载，下载请点击。(下载需要1个积分，下载完评论资源你就可以赚回那1积分，相当于没损失)。请原谅博主的这一点点自私。两个程序得效果如下：
粒子滤波从推导到应用这个系列到这里就结束了。结合前面几章的问题起来看，基本的粒子滤波里可改进的地方很多，正由于此才诞生了很多优化了的算法，而这篇博客只理顺了基本算法的思路，希望有帮到大家。
另外，个人感觉粒子滤波和遗传算法真是像极了。同时，如果你觉得这种用很多粒子来计算的方式效率低，在工程应用中不好接受，推荐看看无味卡尔曼滤波（UKF）,他是有选择的产生粒子，而不是盲目的随机产生。
ps:今年上半年的时候就很想写这篇博客了，但是每次看到那么多公式，实在有点不愿意去敲。到最近又用到，才下了决心，希望以后自己改了这个毛病，扎扎实实的做好每一步，不眼高手低。
（转载请注明作者和出处：http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途）
reference：
1.M. Sanjeev Arulampalam 《A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking》