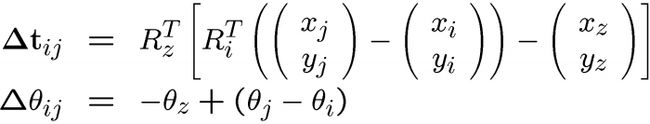graph slam tutorial ：从推导到应用3
对于二维平面的激光SLAM，数据包括两部分，odometry和laser range data，所以构图过程如下：
- 当机器人前进0.5m或者旋转超过0.5弧度时，将新的机器人位姿添加到图的顶点，并且记录相应的激光数据。
- 当前激光数据和上一次的激光数据进行匹配，通过scan match获得两个相邻位姿之间的变换关系，将该变换关系加入到图的边。
- 当机器人重新回到一个已知区域时，激光数据和以前的诺干组数据进行匹配进行闭环检测。如果匹配成功，在相应顶点之间加入一条边。
对于3D的SLAM图优化的前端和上述过程基本差不多。
图优化后端
1.构建误差函数
在构建好图以后，就得根据误差函数求雅克比矩阵，然后根据雅克比矩阵求b以及系统信息矩阵H了。对于2维SLAM，我们知道机器人某一时刻的位姿可以表示成。在各类论文中（主要是弗莱堡大学Grisetti派系的），把误差函数设定为如下形式：
其中函数t2v()表示将位姿矩阵转为向量，直接看代码。
% A = cos -sin x % sin cos y % 0 0 1 % v = (x,y,theta) function v = t2v(A) % T2V homogeneous transformation to vector v(1:2,1) = A(1:2,3); % 第三列第1,2行，即x,y v(3,1) = atan2(A(2,1), A(1,1)); end
并且上式中
是位姿向量的矩阵形式，使用一个v2t()的函数就行了。
function A = v2t(v)
% V2T vector to homogeneous transformation
c = cos(v(3));
s = sin(v(3));
A = [c, -s, v(1);
s, c, v(2);
0 0 1];
end
误差函数表达式中要注意
表示位姿j到位姿i之间的变换矩阵
，也可以说是坐标j和坐标i之间的差异，至于为什么这里两个矩阵相乘就能表示它们的差异，这是由于它们是位姿矩阵，看下面的分析。
先来一个简单版的推导:
表示位姿i在世界坐标系w中的表示,也表示将坐标系i中的一点转换到世界坐标系w中的转换矩阵，同理表示坐标系j中的一点转换到世界坐标系w中的转换矩阵，也可以说是坐标系j在世界坐标系w中的表示。
现在可以看看那两个矩阵相乘的含义了：
，最后的结果是Xij，而它表示的就是坐标系j到坐标系i的转换矩阵。
上面这个推导用下标推算简单说明了情况，背后的数学推导还是有必要看看的。现在开始严格一点的数学推导。我们先不分析，分析
和分析是一样的，所以直接分析，即为什么测量出的转换矩阵和理论计算的转换矩阵的误差err要这样计算？
预备知识：对于分块矩阵如何求逆。
现在开始推导。不妨假设j到i变换的变换矩阵估计值为：
注意，矩阵中的组成分别是旋转矩阵R和平移向量t。i,j之间变换的测量值变换矩阵为：
误差计算：
误差计算中最后一步是把上面的矩阵向量化。
旋转矩阵
表示逆时针旋转，表示顺时针旋转，
两个旋转矩阵相乘再向量化的物理意义不就是两个旋转矩阵角度的差异嘛。而
表示两个位移向量的差异。因此，同理也表示位姿j到位姿i之间的变化。
2.计算雅克比矩阵
误差函数有了，接下来最重要的一步是计算雅克比矩阵，先把误差函数由矩阵形式一步一步向量化，先把如下
将上面的矩阵再进一步转化为误差向量。
把上面的误差向量对机器人位姿i求偏导得到Aij。先对平移向量
求偏导，再对角度
求偏导得
同理，对位姿j求偏导得到Bij。
程序中对应的计算如下：
%compute the homoeneous transforms of the previous solutions zt_ij = v2t(z_ij);%向量转化为矩阵 vt_i = v2t(v_i); vt_j = v2t(v_j); %compute the displacement between x_i and x_j f_ij=(inv(vt_i) * vt_j);% Xi的逆乘以Xj %this below is too long to explain, to understand it derive it by hand theta_i = v_i(3); ti = v_i(1:2,1); tj = v_j(1:2,1); dt_ij = tj-ti; si = sin(theta_i); ci = cos(theta_i); % 这里的A，B是还没有乘以Rz转置的 A= [-ci, -si, [-si, ci]*dt_ij; si, -ci, [-ci, -si]*dt_ij; 0, 0, -1 ]; B =[ ci, si, 0 ; -si, ci, 0 ; 0, 0, 1 ]; ztinv = inv(zt_ij); e = t2v(ztinv * f_ij); % 误差向量 ztinv(1:2,3) = 0;% 偏导A,B计算公式中只用了z的旋转矩阵R，所以把平移向量强制清0 A = ztinv*A; % 乘以Z的转置，即Z的逆，这是由于旋转矩阵的关系 B = ztinv*B;有了雅克比矩阵以后，只要将计算的b,H累加起来就行了
对应代码如下：
%compute the blocks of H^k
b_i = -A' * omega * e;
b_j = -B' * omega * e;
H_ii= A' * omega * A;
H_ij= A' * omega * B;
H_jj= B' * omega * B;
%accumulate the blocks in H and b
H((id_i-1)*3+1:id_i*3,(id_i-1)*3+1:id_i*3) = ...
H((id_i-1)*3+1:id_i*3,(id_i-1)*3+1:id_i*3)+ H_ii;
H((id_j-1)*3+1:id_j*3,(id_j-1)*3+1:id_j*3) = ...
H((id_j-1)*3+1:id_j*3,(id_j-1)*3+1:id_j*3) + H_jj;
H((id_i-1)*3+1:id_i*3,(id_j-1)*3+1:id_j*3) = ...
H((id_i-1)*3+1:id_i*3,(id_j-1)*3+1:id_j*3) + H_ij;
H((id_j-1)*3+1:id_j*3,(id_i-1)*3+1:id_i*3) = ...
H((id_j-1)*3+1:id_j*3,(id_i-1)*3+1:id_i*3) + H_ij';
b((id_i-1)*3+1:id_i*3,1) = ...
b((id_i-1)*3+1:id_i*3,1) + b_i;
b((id_j-1)*3+1:id_j*3,1) = ...
b((id_j-1)*3+1:id_j*3,1) + b_j; 所有部分计算完毕以后，就是计算增量，迭代直到收敛。
下面是matlab代码中，图优化前和优化后的机器人轨迹对比：
整个代码是grisetti课程里面代码改成的matlab版。我不生产代码，只是github的搬运工，O(∩_∩)O 下载地址戳这里。在看代码前，建议看看关于图顶点和边的数据说明。
图的数据格式
最后讲一下图优化前端处理以后产生的顶点和边的数据格式，这是写程序时特别关注的，也是众多优化包如g2o的数据格式。
顶点vertex2: id，pose.x，pose.y，pose.theta 其中id表示位姿的序号，后面三个是位姿参数
边EDGE2: idFrom idTo mean.x mean.y mean.theta inf.xx inf.xy inf.yy inf.xt inf.yt inf.tt 其中idfrom,idTo表示连接边的两个位姿顶点序号，mean.xytheta表示测量的位姿变换矩阵。inf表示边的信息矩阵即权重。
到目前为止，基本已经了解了graph based slam是咋回事。在实际编程中，弗莱堡大学的牛人们开发了g2o优化包帮大家解决图优化的后端（back-end)问题。因此写写图优化前端的程序（match,icp求位姿矩阵,loop closure），构建图，然后再用g2o库就能够完成一个图优化SLAM程序，是不是感觉思路很清晰，很容易。关于g2o库的使用，Grisetti写了一个教程，g2o也自带很多例子，但是不自己动动手，永远给人感觉像是雾里看花，水中望月，不踏实。在下一篇博客中，我们将拿一个数据集练练手，操练操练g2o库的使用，祝好运。
（转载请注明作者和出处：http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途）
reference：
1. Grisetti的课程，有课件下载，点这里
2. Grisetti. 《A Tutorial on Graph-Based SLAM》
3. Grisetti. 课件 《SLAM Back-end》（可以直接搜到）