(三)数据结构
动态集合的操作:查询操作,修改操作。
第十章 基本数据结构
栈(LIFO)和队列(FIFO)
采用数组来实现两种数据结构
栈的实现
思想:首先判断是否为空栈,然后实现push元素,通过判断是否为空栈,来确定pop元素
Stack-empty(S)
{
if top[S] = 0
then return TRUE
else
return FALSE
}
Push(S,x)
{
top[S] = top[S] +1
S[top[S]] = x
}
Pop(S)
{
if Stack-empty(S)
then error "enderflow"
else
top[S] = top[S]-1
return S[top[S]+1]
}
队列的实现
思想:将元素入队列,将元素放到队列末尾,如果到达最后一个位置,再将其重置,通过tail[Q]来插入元素。出队列是将头元素做出出列元素,然后让后面一个覆盖这个要出列的的元素。
Enqueue(Q,x)
{
Q[tail[Q]] = x
if tail[Q] = length[Q]
then tail[Q] =1
else tail[Q] = tail[Q]+1
}
Dequeue(Q)
{
x = Q[head[Q]]
if head[Q] = length[Q]
then head[Q] =1
else head[Q] = head[Q]+1
return x
} 注:防止溢出(可用判断语句来判断是否溢出,来解决这个问题,来可以指针的形式来不断申请空间来防止溢出)
链表:双链表,带哨兵的环形双链表
思想:搜索操作通过头元素开始,往下搜索;插入操作通过往头元素前面插入一个新元素;删除操作,删除头元素。
//双链表
//搜索操作
List-search(L,k)
{
x = head[L]
while x != Nil and key[x] != k
do x = next[x]
return x
}
//插入操作
List-insert(L,x)
{
next[x] = head[L]
if head[L] != Nil
then prev[head[L]] = x
head[L] = x
prev[x] =Nil
}
//删除操作
List-delete(L,x)
{
if prev[x] != Nil
then next[prev[x]] = next[x]
else
head[L] = head[x]
if next[x] != Nil
then prev[next[x]] = prev[x]
}
//环形双链表
//哨兵用nil[L]表示
//删除操作
List-delete(L,x)
{
next[prev[x]] = next[x]
prev[next[x]] = prev[x]
}
//查找操作
List-search(L,k)
{
x = next[nil[L]]
while x != nil[L] and key[x] != k
do x = next[x]
return x
}
//插入操作
list-insert(L,x)
{
next[x] = next[nil[L]]
prev[next[nil[L]]] = x
next[nil[L]] = x
prev[x] = nil[L]
} 指针和对象的实现:
第一种方法:用对象的多重数组来表示
思想:建立三维数组来实现
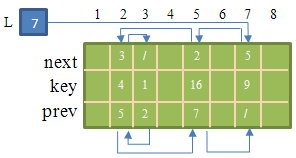
第二种方法:用对象的单数组来表示
思想:通过三个连在一起的三个元素,第一个表示key,第二个表示prev[key]元素,第三个表示next[key],来实现数组
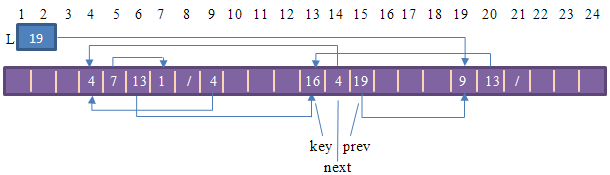
分配和释放对象
思想;通过把自由对象安排成一个单链表,成为自由表,通过自由表与数组交错在一起,然后用插入和删除的操作来分配和释放对象。
Allocate-object()
{
if free = Nil
then error"out of space"
else
x = free
free = next[x]
return x
}
Free-object(x)
{
next[x] = free
free = x
}
二叉树通过域p,left,right来存放指向二叉树的T中父亲,左儿子,右儿子
分支数无限制的有根数
树的其他表示。
第十一章 散列表
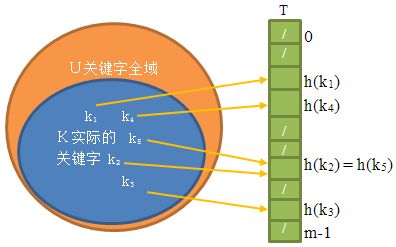
直接寻址表
思想:通过直接寻址表T[0....m-1],每个位置对应全域U的一个关键字,如果没有关键字,就设定nil(针对域U比较小的)
Direct-address-search(T,k)
return T[k]
Direct-address-insert(T,x)
T[key[x]] = x
Direct-address-delete(T,x)
T[key[x]] = Nil
散列表
利用散列函数h,根据h来计算槽的位置。即函数h将关键字域U映射到散列表T[0....m-1]的槽位上:h:U --> {0.1.2.......m-1}
通过上面方法,我们可能会碰到一个“”碰撞“问题,即两个关键字可能映射到同一槽上。
解决办法:一,链接法
二,开放寻址发
链接法实现:
Chained-hash-insert(T,x) insert x at the head of list T[h(key[x])] Chained-hash-search(T,x) search for an element with key k in list T[h(k)] Chained-hash-insert(T,x) delete x from th list T[h(key[x])]
散列函数
三种方案:一,除法散列;二,乘法散列;三,全域散列(利用随机化技术)
第一步:将关键字解释为自然数
第二步:采用除法散列:h(k) = k mod m
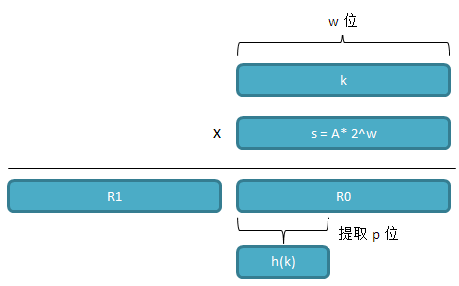
采用乘法散列:h(k) = m(kA mod 1)
操作:1、将k与s相乘,它将得到一个2*w位的乘积,值形如R1*2^w + R0;
2、对低w位的R0,取高位的p位,便是散列后的结果。(涉及到计算机乘法原理及比特位)
采用全域散列:为了尽可能地避免最坏情况的发生,我们不使用某个特定的散列函数,而是准备好一系列的散列函数,在执行开始时随机选择一个作为之后的散列函数。
设H为有限的一组散列函数,它将给定的关键字域U映射到{0, 1, ..., m-1}中,这样的一个函数组称为是全域的(universal),如果它满足以下条件:
对每一对不同的关键字k,l ∈ U,满足h(k) = h(l)的散列函数h∈H的个数至多为|H| / m。换言之,如果从H中随机选择一个散列函数,当k≠l时,两者发生碰撞的概率不大于1/m。
对使用全域散列函数的散列表,其用链接法处理碰撞的,包含某关键字k的链表的期望长度至多为1+a,其中a为装载因子。
设计一个全域散列函数函数类:
选择一个足够大的质数p,使得每一个可能的关键字k都落在0到p-1的范围内,设Z_p表示集合{0,1,2,.......,p-1},设Z_p*表示{1,2,......,p-1},
对于任何a∈Z_p*,和任何b∈Z_p,定义散列函数:
h_a_b (k) = ((a*k+b) mod p) mod m
所有这样的散列函数构成的函数簇为:
H_p_m = {h_a_b:a∈Z_p*和b∈Z_p}
开放寻址法:所有元素都存放在散列表里,每个表项或包含一个元素,或包含NIL,但不会包含链表或其它的处于散列表外的辅助结构。
当插入一个元素时,如果映射的位置已经被其它元素占用,则通过散列函数再产生另一个映射值(称为探查),直到找到空槽或发现表中没有空槽为止。
对开放寻址法来说,要求对每一个关键字k,探查序列{h(k, 0), h(k, 1), ..., h(k, m-1)}必须是{0, 1, ..., m-1}的一个排列,即散列函数h在连续对同一个关键字k进行散列时,每次得到的都是不一样的值。
Hash-insert(T, k)
{
i = 0
do {
j = h(k, i);
if T[j] == NIL {
T[j] = k;
return j;
}
else
i += 1;
} while i≠m
error "hash table overflow"
}
Hash-search(T, k) {
i = 0;
do {
j = h(k, i);
if (T[j] == k)
return j;
else
i += 1;
} while i ≠ m and T[j] ≠ NIL
return NIL;
}
删除操作执行起来比较困难,当我们从槽i中删除关键字时,不能简单地让T[i]=NIL,因为这样会破坏查找的过程。假设关键字k在i之后插入到散列表中,如果T[i]被设为NIL,那么查找过程就再也找不到k了。解决这个问题的方法是引入一个新的状态DELETED,而不是NIL,这样在插入过程中,一旦发现DELETED的槽,便可以在该槽中放置数据,而查找过程不需要任何改动。但如此一来,查找时间就不再依赖于装载因子了,所以在必须删除关键字的应用中,往往采用链接法来解决碰撞。
有三种技术常用来计算开放寻址法中的探查序列:线性探查、二次探查和双重探查。
给定一个普通的散列函数h':U→ {0, 1, ..., m-1}(称为辅助散列函数),线性探查(linear probing)方法采用的散列函数为:
h(k, i) = (h'(k) + i) mod m, i = 0, 1, ..., m-1
它在碰撞发生后,便依次探查当前槽的后一个槽,到T[m-1]后绕回到T[0]继续探查,直到最开始发生碰撞的槽的前一个槽。
线性探查方法比较容易实现,但它存在一个问题,称作一次群集(primary clustering)。随着时间的推移,连续被占用的槽不断增加,平均查找的时间也随着不断增加。
二次探查(quadratic probing)采用如下形式的散列函数:
h(k, i) = (h'(k) + c1*i + c2*i^2) mod m
c1和c2为常量。这种探查方法的效果比线性探查好很多,但c1, c2, m的取值受到限制。此外,如果两个关键字的初始探查位置相同,那么它们的探查序列
也是相同的,即h(k1, 0) = h(k2, 0)意味着h(k1, i) = h(k2, i),这一性质可导致一种程度较轻的群集现象,称为二次群集(secondary clustering)。
h(k, i) = (h1(k) + i*h2(k)) mod m
为了能查找整个散列表,值h2(k)要与表的大小m互质。有两种方法:1、m为2的幂,而h2总产生奇数;2、取m为质数,h2则总是产生比m小的正整数。
线性探查和二次探查都只能产生m种不同的序列,而双重散列可以产生m^2种,这样已经与“理想的”一致散列的性能很接近了。
开放寻址法的性能分析:一次成功的查找平均需要探查的次数为1/a * ln(1/(1-a))。
Inorder-tree-walk(x) { //中序遍历法
if x ≠ NIL {
Inorder-tree-walk(left[x]);
print key[x];
Inorder-tree-walk(right[x]);
}
}
Tree-search(x, k) { //递归版本二叉查找树
if x == NIL or key[x] == k
return x
if k < key[x]
return TREE_SEARCH(left[x], k)
else
return TREE_SEARCH(right[x], k)
}
Iterative-tree-search(x, k) { //非递归版本二叉查找树
while x ≠ NULL and k ≠ key[x] {
if (k < key[x])
x = left[x]
else
x = right[x]
}
return x
}
运行时间:T(n) = O(n)
TREE_MINIMUM(x) { //min
while left[x] != NIL
x = left[x]
return x;
}
TREE_MAXIMUM(x) { //max
while right[x] != NIL
x = right[x];
return x;
}
TREE_SUCCESSOR(x) { //predecessor and successor
if right[x] ≠ NIL {
return TREE_MINIMUM(right[x]); //predecessor
y = parent[x];
while y ≠ NULL and x ≠ left[x]
{
x = y;
y = parent[x];
}
return y; //successor
}
二叉树的插入和删除
Tree-insert(T, z) { //insert
x = NIL;
y = root[T];
while y ≠ NIL {
x = y;
if key[z] ≤ key[y]
y = left[y];
else
y = right[y];
}
if x == NIL // tree was empty
root[T] = z;
else
if key[z] ≤ key[x]
left[x] = z;
else
right[x] = z;
}
Tree-delete(T, z) { //delete
if left[z] == NIL or right[z] == NIL
y = z;
else
y = TREE_SUCCESSOR(z);
if left[y] ≠ NIL
x = left[y];
else
x = right[y];
if x ≠ NIL
p[x] = p[y];
if p[y] == NIL
root[T] = x;
else if y == left[p[y]]
left[p[y]] = x;
else
right[p[y]] = x;
if y ≠ z {
key[z] = key[y];
copy y's satellite data into z;
}
return y;
}
3、如果要删除的结点有两个子女,则找到它的后继(右子树的最左结点)来代替这个被删除结点。(之所以这么做,因为它的后继比它的左子树的所有元素都大,又比它的右子树中的所有其它元素小。)
对于高度h的二叉查找树,气动态集合insert,和delete的运行时间为O(h)
红黑树的性质
1、每个结点或是红的,或是黑的。
2、根结点是黑的。
3、每个叶结点(NIL)是黑的。
4、如果一个结点是红的,则它的两个儿子都是黑的。
5、对每个结点,从该结点到其子孙的所有路径上包含相同数目的黑结点。
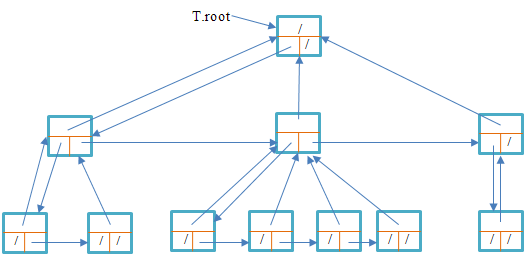
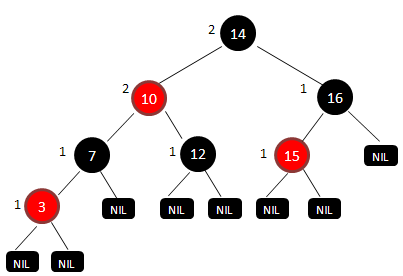
一颗红黑树:
可以看到所有的叶结点都是NIL,且都是黑的。这些叶结点被称为外结点,除了外结点的其它结点便被称为内结点。所有内结点旁标注的数字是该结点的黑高度,即从该结点出发到达一个叶结点的任意一条路径上的黑色结点的个数(根据性质5所有路径上黑结点个数一样)。
因为所有的叶结点都是一样的,所以我们可以用一个哨兵元素来表示它:
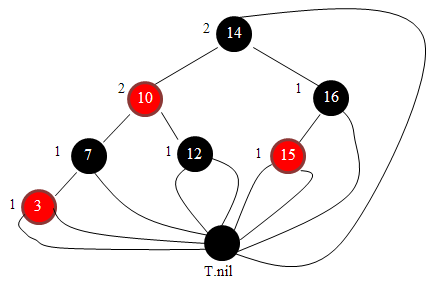
根结点的父亲也可以使用这个哨兵元素。
红黑树的高度为O(lg(n))。
旋转:我们可以通过旋转来改变某些结点在树中的位置而不破坏二叉查找树的性质。
左旋转代码:
Left-rotation(T, x) {
y = right[x];
right[x] = left[y];
if left[y] ≠ nil[T]
p[left[y]] = x;
p[y] = p[x];
if p[x] == nil[T]
root[T] = y;
else if x == left[p[x]]
left[p[x]] = y;
else
right[p[x]] = y;
left[y] = x;
p.[x] = y;
}
右旋转代码:
Right-rotation(T,x)
{
y = left[x]
left[x] = right[y]
if right[y] != Nil[T]
right[y] =x
p[y] = p[x]
if p[x] = Nil[T]
root[T] = Nil[T]
else if x = left[p[x]]
left[p[x]] = y
else
right[p[x]] = y
p[x] = y
}
插入操作
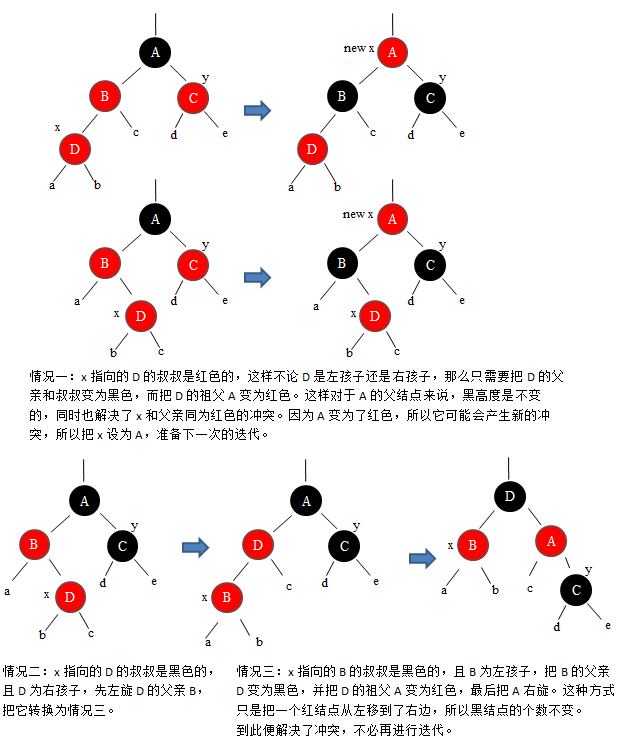
思想:首先把树当做普通的二叉查找树,将节点x插入进去,然后通过一个辅助函数RB-insert-fixup来对节点重新着色并旋转
其三种情况如图:
代码:
RB_insert(T, z) {
y = NIL[T];
x = root[T];
while x != NIL[T] {
y = x;
if key[z] < key[x]
x = left[x];
else
x = right[x]
}
p[z] = y;
if y == nil[T]
root[T] = z;
else if key[z] < key[y]
left[y] = z;
else
right[y] = z;
left[z] = nil[T];
right[z] = nil[T];
color[z] = RED;
RB-insert-fixup(T, z);
}
//辅助函数
RB-insert-fixup(T, z) {
while color[p[z]] == RED {
if p[z] == left[p[p[z]]] {
y = right[p[p[z]]];
// CASE 1
if color[y] == RED {
color[p[z]] = BLACK;
color[y] = BLACK;
color[p[p[z]]] = RED;
z = p[p[z]];
}
// CASE 2
else if z == right[p[z]] {
z = p[z];
Left-rotation(T, z);
}
// CASE 3
color[p[z]] = BLACK;
color[p[p[z]]] = RED;
Right-rotation(T, p[p[z]]);
}
// z's parent is a right child
else
same as the previous "if" clause with "right" and "left" extranged.
}
color[root[T]] = BLACK;
}
其插入 操作索要花的时间是O(lg(n))
删除操作
思想:首先把树当做普通的二叉查找树,将节点x删除,然后通过一个辅助函数RB-insert-fixup来改变节点的颜色并做选装,从而保持红黑树的性质
四种情况如图:
代码:
RB-delete(T, z) {
if left[z] == nil[T] or right[z] == nil[T]
y = z;
else
y = SUCCESSOR(z);
if left[y] != nil[T]
x = left[y];
else
y = right[y];
p[x] = p[y];
if p[y] == NIL[T]
root[T] = x;
else if y == left[p[y]]
left[p[y]] = x;
else
right[p[y]] = x;
if y != z {
key[z] = key[y];
copy y's satellite data into x;
}
if color[y] == BLACK
RB-delete-fixup(T, x);
return y;
}
RB-delete-fixup(T, x) {
while x != root[T] and color[x] == BLACK {
if x == left[p[x]] {
// CASE 1
w = right[p[x]]; // brother
if color[w] == RED {
color[w] = BLACK;
color[p[x]] = RED;
Left-rotation (T, p[x]);
w = right[p[x]];
}
// CASE 2
if color[left[w]] == BLACK and right[right[w]] == BLACK {
color[w] = RED;
x = p[x];
}
// CASE 3
else if color[right[w]] == BLACK {
color[left[w]] = BLACK;
color[w] = RED;
Right-rotation(T, w);
w = right[p[x]];
// CASE 4
color[w] = color[p[x]];
color[p[x]] = BLACK;
color[right[w]] = BLACK;
Left-rotation(T, p[x]);
x = root[T];
}
}
else
same as the previous "if" clause with "right" and "left" exchanged;
}
color[x] = BLACK;
}
w-s运行时间:O(lg(n))
第十四章 数据结构的扩张
动态顺序统计
思想:将红黑树改装,增加一个域,即size[x]域即子数的大小
检索具有给定排序的元素
OS_SELECT(x, i) {
r = size[left[x]] + 1;
if i == r
return x;
else if i < r
return OS_SELECT(left[x], i);
else
return OS_SELECT(right[x], i-r);
}
确定一个元素的秩
思想:x的秩可以视为在对树的中序遍历中,排在x之前的节点个数再加上1
Os-rank(T, x) {
1 r = size[left[x]] + 1;
2 y = x;
3 while (y != root[T])
{
4 if y == right[p[x]]
5 r = size[left[p[y]]] + 1;
6 y = y.parent;
7 }
8 return r;
}
对子树规模的维护
在插入元素时,分两阶段,阶段一:从根开始向下遍历,直到元素找到可以插入的位置;阶段二:通过旋转来维护红黑性质。在阶段一,我们只需在遍历时经由的所有结点的size增加1便可,时间为O(lg(n)),在阶段二最多会有O(lg(n))次旋转,每次旋转只需O(1)的时间:重新计算被旋转的元素的size,看下图:
在LEFT_ROTATE里加入下列两行代码以维护size信息:
size[y] = size[x]; size[x] = size[left[x]] + size[right[x]] + 1
综上所述,插入元素的两个阶段里,维护size息共需O(lg(n))的时间。
同样,在删除元素时,同样分为两个阶段,阶段一:从树中删除元素,阶段二,通过旋转维护红黑信息。对于阶段一,我们可以沿着被删除的元素一直向根遍历,经由的每个结点的size域都减1;在阶段二至多有O(lg(n))次旋转。所以删除操作时维护size域的运行时间同样为O(lg(n))。
如何扩张数据结构
对一种数据结构的扩张过程可分为四个步骤:
1、选择基础数据结构; (选择红黑树)
2、确定要在基础数据结构中添加哪些信息; (加入size域)
3、验证可用基础数据结构上的基本修改操作来维护这些新添加的信息; (插入和删除可以维护size域)
4、设计新的操作。 (OS_SELECT和OS_RANK)
以上给出的是一般模式,不必生硬地遵循。
区间树
区间树中,每个结点的关键字不是简单的整数,而是一个区间[low, high],域名key同样也更名为interval。在进行关键字比较时,low更小的值作为更小的值放在树的左侧。同时,每个结点还维护一个max域,它表示以该结点为根的子树里,所有元素里的区间[low, high]的high值中的最大值。
我们这样定义两个区间重叠(overlap):[low, high]和[low', high']只有在high < low'或high' < low时才不重叠。
基于这个数据结构,我们可以定义一个新操作:给定一个区间i,查找区间树中与i重叠的区间:
Interval-search(T, i)
{
x = root[T];
while x != nil[T] and i does not overlap interval[x] {
if left != nil[T] and max[left[x]] >= low[i]
x = left[x];
else
x = right[x];
}
return x;
}