算法导论第32章 字符串匹配

书中依次讲了4种方法，朴素算法、RabinKarp算法、有限自动机算法、KMP算法

1、朴素算法：

算法用一个循环来找出所有有效位移，该循环对n-m+1个可能的每一个s值检查条件P[1...m] = T[s+1....s+m];

//朴素的字符串匹配算法
void nativeStringMatcher(string st, string sp)
{
	int n = st.length();          //主串长度
	int m = sp.length();          //模式串长度

	for (int s = 0; s <= n-m+1; s++)
	{
		string ss = st.substr(s, m);   //ss为st从s位置开始的m个字符，即和sp比较的字符串
		if (sp == ss)
			cout << "在位置" << s << "处发现匹配" << endl;
	}
}

算法运行时间为O（（n-m+1）m），循环运行n-m+1次，每次最多比较m次。

2、RabinKarp算法：算法思想是将字符串映射到一个数字，然后比较字串的数字是否相等，如果相等则继续进一步判断确认正确性，如果不相等，则可以判断字符串不匹配。

书中为了说明方便，采用的是十进制的数制，

已知一个模式P[1...m],设p表示其相应的十进制数的值，对于给定的文本T[1....n],用ts表示长度为m的子字符串T[s+1....s+m] (s=0,1...n-m+1)相应的十进制的值。

ts = p当且仅当T[s+1....s+m] = P[1,2...m].

可以运用霍纳法则在O(m)时间内计算p的值：  p = P[m] + 10(P[m-1] + 10(P[m-2])+....+10(P[2]+10P[1]).....)

类似的，可以在O（m）时间内根据T[1,2....m]，计算出t0,

为了在O（n-m）时间内计算出剩余的值t1,t2,....tn-m,可以在常数时间内根据ts计算出t（s+1），

                                     t（s+1） = 10（ts - 10（m-1次方）* T[s+1]） + T[s+m+1]

减去 10（m-1次方）* T[s+1]，就是从ts中去掉了高位数组，再把结果乘以10，就使数左移了一位，然后在加上T[s+m+1],就加入一个适当的低位数。

这要预先算出常数 10（m-1次方）（不同进制不一样，不同的映射方法也不一样）

这样可以在O（m）的时间内算出p，在O（n-m+1）时间算出t0, t1....tn-m,所以可以用O（m）的预处理时间和O（n-m+1）时间内算出匹配位置。

这个过程的问题是p和ts的值可能过大，所以可以选择一个合适的模q来计算p和ts的模。

一般情况下，采用d进制的字母表{0, 1,...d-1}时，所选取的q要满足使dq的值在一个计算机字长内，并调整递归式使其对模q进行运算，

                                                        t（s+1） = （d（ts - T[s+1]h）+  T[s+m+1]）mod q

其中h = d (m-1次方）是一个m数位文本窗口中高伟数位上的数字“1”的值。

但是加入模q后，存在伪命中，还需要进一步判断。如果q足够大，伪命中就比较少，额外检查的代价就低 、

下图是关于算法的说明：

代码为：

//RK算法，映射方法
void RabinKarpMatcher(string st, string sp, int d, int q)
{
	int n = st.length();
	int m = sp.length();
	int h = 1;        //初始化为m位数字中高位数字的值
	int p = 0;        //sp字符串对应的数字的值
	int t = 0;        //st中每m个连续字符串对应的数组的值
	int i;

	//m位数字中的最高位的权值，例如10进制5位数，该值为10000
	for(i = 0; i < m-1; i++)
		h = (h * d) % q;

	//计算p值，t值
	for (i = 0; i < m; i++)
	{
		p = (p * d + (sp[i] - 'a')) % q;
		t = (t * d + (st[i] - 'a')) % q;
	}

	//开始进行匹配，如果算出的值相等，则进一步判断是否相等，
	//否则，不匹配，计算下一个m位字符串对应的值，继续循环
	//计算方法为：t(s+1) = (d*(t(s) - T[s+1]*h) + T[s+m+1]) mod q
	for (int s = 0; s < n-m+1; s++)
	{
		if (p == t && sp == st.substr(s, m))
		    cout << "在位置" << s << "处发现匹配" << endl;
		int tmp = t;
		t = (d * (tmp - (st[s]-'a')*h) + st[s+m]-'a') % q;
	}
}

虽然算法在最坏情况下时间为O（（n-m+1）m），但是适当选取q可以时伪命中降低很多，运行时间可以为O（n+m）

3、有限自动机，没完全明白，，不写了

4、KMP算法：算法时间为O（n），利用了辅助数组p[1.2....m],它是在O（m）内根据模式预先算出来的，

模式的前缀字符p包含有模式与其自身的位移进行匹配的信息，这些信息可以避免在朴素的字符串匹配算法中，对无效位移进行测试

已知模式字符P[1...q]与文本字符T[s+1...s+q]匹配，那么满足  P[1...k] = T[s'+1...s'+k],其中s'+k = s+q的最小位移s' > s是多少，

对于新位移，无需把P的前k个字符与T中相应的字符进行比较，因为前面的等式已经满足了。

可以用模式与其自身进行比较，以预先计算出这些必要的信息，由于T[s'+1...s'+k]是文本中已经知道的部分，所以它是字符串Pq的一个后缀，

可以将 P[1...k] = T[s'+1...s'+k]解释为满足Pk是Pq的后缀的最大的k < q,于是，s' = s+（q-k）就是一个可能的有效位移。

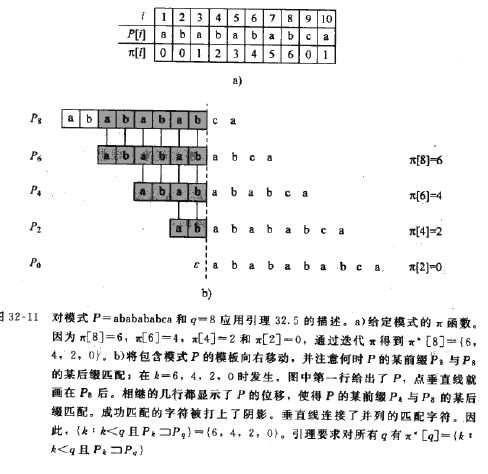
以下是预计算过程的形式化说明。已知一个模式P[1...m]，模式P的前缀函数是函数p{1，2...m}->{0，1，...,m-1}并满足

p[q] = max {k: k < q 且 Pk是Pq的后缀}          p[q]是Pq的真后缀P的最长前缀的长度。

以下图片帮助理解：

代码如下：

//计算前缀数组，将模式与自身进行比较
void computePrefixFunction(string sp, int *p)
{
	int m = sp.length();
	p[0] = 0;
	int k = 0;    //匹配的字符数

	for (int q = 1; q < m; q++)    //循环模式sp
	{
		while (k > 0 && sp[k] != sp[q]) //不相等，k向后减，直到字符匹配或k = 0
			k = p[k-1];
		if (sp[k] == sp[q])       //如果相等k后移
			k++;
		p[q] = k;
	}
	cout << "计算出来的前缀数组是：" << endl;
	for (int i = 0; i < m; i++)
		cout << p[i] << " ";
	cout << endl;
}

//KMP算法
void KMPMatcher(string st, string sp)
{
	int n = st.length();
	int m = sp.length();

	int *p = new int[m];
	computePrefixFunction(sp, p);

	int q = 0;      //匹配的字符数
	for (int i = 0; i < n; i++)     //从左到右扫描st
	{
		while (q > 0 && sp[q] != st[i])   //当当前字符串不匹配，迭代求解q的值
			q = p[q-1];                   //即下一个p中与s[i]匹配的位置
	    if (sp[q] == st[i])    //如果当前字符匹配，则q后移
			q++;
		if (q == m-1)
		{
			cout << "Pattern occurs with shift " << i-m+1 << endl;
			q = p[q];
		}
	}
	delete [] p;
}

算法对st只扫描一遍，当不匹配时，从数组p中取出sp中下一个应该与st中不匹配字符比较的索引，所以运行时间为O（n），预处理时间为O（m）