0-1背包、多重背包、钢条问题分析
0-1背包、多重背包、钢条问题这都是属于动态规划的范畴。
0-1钢条问题
问题描述:给定一段长度为n的钢条和一个价格表p(i)(i=1,2,3,4…n),p(i)表示长度为i的钢条的价格,求切割方案,使得收益r(n)最大。
很显然我们可以通过更短钢条的收益来描述r(n),r(n)=max{r(n-1)+r(1),r(n-1)+r(2),…,r(1)+r(n-1)}
代码描述:
1、求最大收益
自顶向下
自底向上
0-1背包问题
为题描述:给定一个背包,容量为n,有编号为1~m的不同的石头各一块,每种石头有着各自的体积和重量,现在需要将石头放到背包中,问怎样使背包中装下重量最多的石头。
dp[i,j]为只考虑编号1~i的石头,在容量为j时可以到达的最大的重量,v[i]为编号为i的是有的所占的体积,w[i]为编号为i的石头的重量。可的总结出以下公式
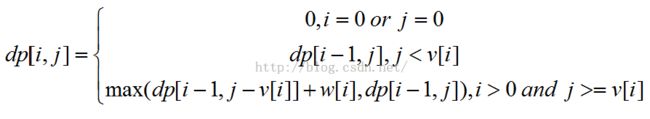
这个公式类似于 LCS的公式,所以该问题的解决方法也和LCS差不多。
代码模板:
自顶向下
2、求具体需要哪些编号的石头
多重背包
问题描述:给定一个背包,容量为n,有编号为1~m的不同的石头,不同编号的石头有着各自的数目,重量,体积,现在需要将石头放到背包中,问怎样使背包中装下重量最多的石头。
代码模板:
1、求能装的最大的重量
自顶向下
2、求具体需要哪些石头和对应的数目
0-1钢条问题
问题描述:给定一段长度为n的钢条和一个价格表p(i)(i=1,2,3,4…n),p(i)表示长度为i的钢条的价格,求切割方案,使得收益r(n)最大。
很显然我们可以通过更短钢条的收益来描述r(n),r(n)=max{r(n-1)+r(1),r(n-1)+r(2),…,r(1)+r(n-1)}
代码描述:
static int n;//钢条长度 static int p[];//价格表,p[i]:长度为i的钢条的价格 static int r[];//r[i]:长度为i的钢条的最大收益
1、求最大收益
自顶向下
static int r(int n)
{
if(n==0) return 0;
int q=-1;
for(int i=1;i<=n;i++)
{
q=Math.max(q, r(n-i)+p[i]);
}
return q;
}缺点:对某些子问题进行多次反复的求解,大大增加了运行时间
自底向上
static void r()
{
for(int i=1;i<=n;i++)
{
r[i]=0;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++){
r[i]=Math.max(r[i],r[i-j]+p[j]);
}
}
}
2、求具体的切割方案
static int[] s;//s[i]:长度为i的钢条切割的第一根钢条的长度
static void r1()
{
for(int i=1;i<=n;i++)
{
r[i]=0;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
if(r[i]<r[i-j]+p[j])
{
r[i]=r[i-j]+p[j];
s[i]=j;
}
}
}
//打印出切割方案
while(n>0)
{
System.out.print(s[n]+" ");
n=n-s[n];
}
}
0-1背包问题
为题描述:给定一个背包,容量为n,有编号为1~m的不同的石头各一块,每种石头有着各自的体积和重量,现在需要将石头放到背包中,问怎样使背包中装下重量最多的石头。
dp[i,j]为只考虑编号1~i的石头,在容量为j时可以到达的最大的重量,v[i]为编号为i的是有的所占的体积,w[i]为编号为i的石头的重量。可的总结出以下公式
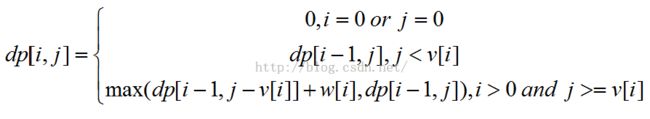
这个公式类似于 LCS的公式,所以该问题的解决方法也和LCS差不多。
代码模板:
static int n;//背包容量 static int m;//石头的总数量 static int v[];//v[i]:编号为i的石头的体积 static int w[];//w[i]:编号为i的石头的重量 static int dp[][];//dp[i][j]:只考虑第编号为1~i的石头,当剩余空间为j时,能达到的最大的重量1、求能装的最大重量
自顶向下
static int dp(int m,int n)//n:剩余容量,m:只考虑编号为1~m的石头
{
if(n==0) return 0;
if(m==0) return 0;
if(n<v[m]) return dp(m-1, n);//剪枝
return Math.max(dp(m-1,n-v[m]),dp(m-1,n));
}自底向上
static void dp(){
for(int i=0;i<=m;i++)
{
dp[i][0]=0;
}
for(int j=0;j<=n;j++)
{
dp[0][j]=0;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(j<v[i])
{
dp[i][j]=dp[i-1][j];
}
else
{
dp[i][j]=Math.max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);
}
}
}
}
2、求具体需要哪些编号的石头
static void print_dp()
{
int j=n;
int s[]=new int[m+1];
for(int i=m;i>=1;i--)
{
if(j<v[i])
{
break;
}
if(dp[i-1][j-v[i]]+w[i]>dp[i-1][j])
{
j=j-v[i];
s[i]=1;
}
}
//打印出用到的石头编号
for(int i=1;i<=m;i++)
{
if(s[i]==1)
{
System.out.print(i+" ");
}
}
}
多重背包
问题描述:给定一个背包,容量为n,有编号为1~m的不同的石头,不同编号的石头有着各自的数目,重量,体积,现在需要将石头放到背包中,问怎样使背包中装下重量最多的石头。
代码模板:
static int n;//背包的容量 static int m;//背包的种类数 static int[] v;//v[i]:编号为i的石头的体积 static int[] w;//w[i]:编号为i的石头的重量 static int[] a;//a[i]:编号为i的石头的数目 static int[][] dp;//dp[i][j]:只考虑编号为1~i的石头,若剩余空间为j,所能达到的最大重量
1、求能装的最大的重量
自顶向下
static int dp(int n,int m)//n:剩余容量,m:只考虑编号为1~m的石头
{
if(n==0) return 0;
if(m==0) return 0;
int tmp=-1;
for(int i=0;i<=a[m];i++)
{
if(n<v[m]*i)
{
break;
}
if(dp(n-i*v[m],m-1)>tmp)
{
tmp=dp(n-i*v[m],m-1)+i*w[i];
}
}
return tmp;
}自底向上
static void dp()
{
int tmp;
for(int i=1;i<=m;i++)
{
tmp=-1;
for(int j=1;j<=n;j++)
{
for(int k=0;k<=a[i];k++)
{
if(j<k*v[i])
{
break;
}
if(dp[i-1][j-k*v[i]]+k*w[i]>tmp)
{
tmp=dp[i-1][j-k*v[i]]+k*w[i];
//j=j-k*v[i];
}
}
dp[i][j]=tmp;
}
}
}
2、求具体需要哪些石头和对应的数目
static void print_dp()
{
int tmp=-1;
int j=n;
int s[]=new int[m+1];//s[i]:编号为i的石头需要的数目
for(int i=m;i>=1;i--)
{
for(int k=0;k<=a[i];k++)
{
if(j<k*v[i])
{
break;
}
if(dp[i-1][j-v[i]*k]+k*w[i]>tmp)
{
tmp=dp[i-1][j-k*v[i]]+k*w[i];
j=j-k*v[i];
s[i]=k;
}
}
}
for(int i=1;i<=m;i++)
{
System.out.print(s[i]+" ");
}
}