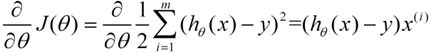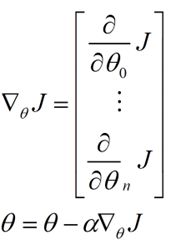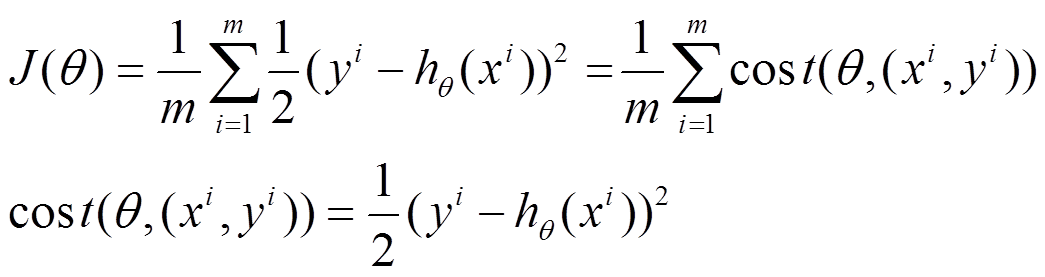梯度下降,随机梯度下降,批量梯度下降,mini-batch 梯度下降
最近在看到一些神经网络优化的问题,
再进行模型的训练的时候,总是希望得到一个能较好的反映实际的模型,在对模型训练的时候其实是在学习其中的参数,
其中主要使用的损失函数来模拟我们的目标,只要使得损失函数可以达到最小或是比较小(可以满足对问题的求解)就行
在对损失函数进行学习时,其实就是找出函数的全局最小解,在此由于问题的不同所产生的损失函数可以是不同的,常见
无非就是凸函数和非凸函数之分。
其中对凸函数一般是可以求得全局最小值的。
对于非凸函数来说,其函数是抖动的,可能存在很多局部解,而在对这类问题求解时可能不能有效地找出其全局最小值,
就把问题的求解退而求其次找出其比较接近全局最小的一个局部最优解。(这一块的理解欠缺,不知道是否正确)
在经过上述求出最优解的过程中,其实就是在不断的迭代学习,将函数中的参数进行定位(值的大小的计算吧),以上jiu
是对整个问题的模型的求解大概过程。
那么问题来了,怎样来将最优解求出来呢?
查阅网上的资料谈论的较多的是最小二乘法和梯度下降法
以下是参考网上的比较
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为:
不同
1.实现方法和结果不同:最小二乘法是直接对
迭代法,即在每一步update未知量逐渐逼近解,可以用于各种各样的问题(包括最小二乘),比如求的不是误差的最小平方和而是最小立方和。
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。高斯-牛顿法是另一种经常用于求解非线性最小二乘的迭代法(一定程度上可视为标准非线性最小二乘求解方法)。
还有一种叫做Levenberg-Marquardt的迭代法用于求解非线性最小二乘问题,就结合了梯度下降和高斯-牛顿法。
所以如果把最小二乘看做是优化问题的话,那么梯度下降是求解方法的一种,
下面的h(x)是要拟合的函数,J(θ)损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(θ)就出来了。
其中m是训练集的记录条数,j是参数的个数。
梯度下降法是按下面的流程进行的:
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
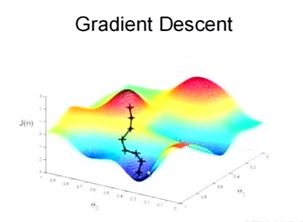
为了更清楚,给出下面的图:
这是一个表示参数θ与误差函数J(θ)的关系图,红色的部分是表示J(θ)有着比较高的取值,我们需要的是,能够让J(θ)的值尽量的低。也就是深蓝色的部分。θ0,θ1表示θ向量的两个维度。
在上面提到梯度下降法的第一步是给θ给一个初值,假设随机给的初值是在图上的十字点。
然后我们将θ按照梯度下降的方向进行调整,就会使得J(θ)往更低的方向进行变化,如图所示,算法的结束将是在θ下降到无法继续下降为止。
当然,可能梯度下降的最终点并非是全局最小点,可能是一个局部最小点,可能是下面的情况:
上面这张图就是描述的一个局部最小点,这是我们重新选择了一个初始点得到的,看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点
下面我将用一个例子描述一下梯度减少的过程,对于我们的函数J(θ)求偏导J:(求导的过程如果不明白,可以温习一下微积分)
下面是更新的过程,也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长,也就是每次按照梯度减少的方向变化多少。
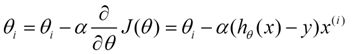 一个很重要的地方值得注意的是,梯度是有方向的,对于一个向量θ,每一维分量θi都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点,不管它是局部的还是全局的。
一个很重要的地方值得注意的是,梯度是有方向的,对于一个向量θ,每一维分量θi都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点,不管它是局部的还是全局的。
用更简单的数学语言进行描述步骤2)是这样的:
下面的h(x)是要拟合的函数,J(θ)损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(θ)就出来了。
其中m是训练集的记录条数,j是参数的个数。
1、批量梯度下降的求解思路如下:
(1)将J( θ)对theta求偏导,得到每个 θ对应的的梯度
(2)由于是要最小化风险函数,所以按每个参数theta的梯度负方向,来更新每个theta
(3)从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果m很大,那么可想而知这种方法的迭代速度!!所以,这就引入了另外一种方法,随机梯度下降。
2、随机梯度下降的求解思路如下:
(1)上面的风险函数可以写成如下这种形式,损失函数对应的是训练集中每个样本的粒度,而上面批量梯度下降对应的是所有的训练样本:
(2)每个样本的损失函数,对theta求偏导得到对应梯度,来更新theta
(3)随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
mini-batch 梯度下降法
(1)将J( θ)对theta求偏导,得到每个 θ对应的的梯度
(2)由于是要最小化风险函数,所以按每个参数theta的梯度负方向,来更新每个theta
(3)从上面公式可以注意到,得到的是一个局部近似解,但是其所计算的时间和效果要比随机梯度下降法的好
但是在计算时候多了一个参数 b 即每批的大小需要去调试。
所以很多的计算使用的是mini-batch梯度下降法来做的。