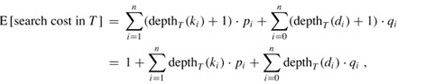算法导论-第15章-动态规划-15.4 最优二叉搜索树
一、什么是最优二叉查找树
最优二叉查找树:
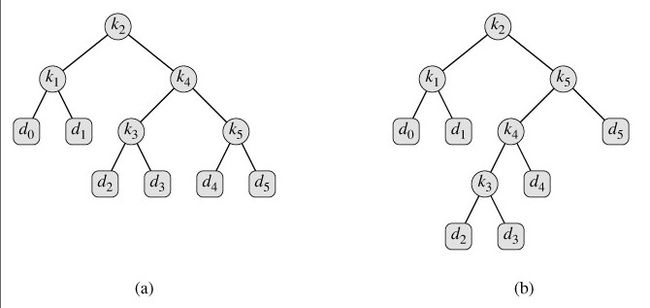
给定n个互异的关键字组成的序列K=<k1,k2,...,kn>,且关键字有序(k1<k2<...<kn),我们想从这些关键字中构造一棵二叉查找树。对每个关键字ki,一次搜索搜索到的概率为pi。可能有一些搜索的值不在K内,因此还有n+1个“虚拟键”d0,d1,...,dn,他们代表不在K内的值。具体:d0代表所有小于k1的值,dn代表所有大于kn的值。而对于i = 1,2,...,n-1,虚拟键di代表所有位于ki和ki+1之间的值。对于每个虚拟键,一次搜索对应于di的概率为qi。要使得查找一个节点的期望代价(代价可以定义为:比如从根节点到目标节点的路径上节点数目)最小,就需要建立一棵最优二叉查找树。
图一显示了给定上面的概率分布pi、qi,生成的两个二叉查找树的例子。图二就是在这种情况下一棵最优二叉查找树。
概率分布:
| i |
0 |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|---|
| pi |
0.15 |
0.10 |
0.05 |
0.10 |
0.20 |
|
| qi |
0.05 |
0.10 |
0.05 |
0.05 |
0.05 |
0.10 |
建立一棵二叉查找树,如果使得上式期望搜索代价最小,那么这棵二叉查找树就是最优二叉查找树。
而且有下式成立:
二、最优二叉查找树的最优子结构
最优子结构:
如果一棵最优二叉查找树T有一棵包含关键字ki,..,kj的子树T',那么这棵子树T'对于关键字Ki,...,kj和虚拟键di-1,...dj的子问题也必定是最优的。可以应用剪贴法证明。
根据最优子结构,寻找最优解:
给定关键字ki,...,kj,假设kr(i<=r<=j)是包含这些键的一棵最优子树的根。其左子树包含关键字ki,...,kr-1和虚拟键di-1,...,dr-1,右子树包含关键字kr+1,...,kj和虚拟键dr,...dj。我们检查所有的候选根kr,就保证可以找到一棵最优二叉查找树。
递归解:
定义e[i,j]为包含关键字ki,...,kj的最优二叉查找树的期望代价,最终要计算的是e[1,n]。
当j = i - 1时,此时子树中只有虚拟键di-1,期望搜索代价为e[i,i - 1] = qi-1.
当j >= i时,需要从ki,...,kj中选择一个根kr,然后分别构造其左子树和右子树。下面需要计算以kr为根的树的期望搜索代价。然后选择导致最小期望搜索代价的kr做根。
现在需要考虑的是,当一棵树成为一个节点的子树时,期望搜索代价怎么变化?子树中每个节点深度都增加1.期望搜索代价增加量为子树中所有概率的总和。
对一棵关键字ki,...,kj的子树,定义其概率总和为:
因此,以kr为根的子树的期望搜索代价为:
![]()
而
因此e[i,j]可以进一步写为:
这样推导出最终的递归公式为:
三、代码实现(C++):
#include <iostream>
using namespace std;
#define N 7
double e[N+2][N+2] = {0};//期望
double w[N+2][N+2] = {0};//概率
int root[N+2][N+2] = {0};//记录树的根结点的位置
/*********调试过程中用于输出中间信息***************************************************/
void PrintE()
{
int i, j;
for(i = 1; i <= N+1; i++)
{
for(j = 1; j <= N+1; j++)
cout<<e[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
void PrintW()
{
int i, j;
for(i = 1; i <= N+1; i++)
{
for(j = 1; j <= N+1; j++)
cout<<w[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
void PrintRoot()
{
int i, j;
for(i = 1; i <= N+1; i++)
{
for(j = 1; j <= N+1; j++)
cout<<root[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
/********书上的伪代码对应的程序******************************************************/
//构造最做树
void Optimal_Bst(double * p, double *q, int n)
{
int i, j, r ,l;
double t;
//初始化。当j=i-1时,只有一个虚拟键d|i-1
for(i = 1; i <= n+1; i++)
{
e[i][i-1] = q[i-1];
w[i][i-1] = q[i-1];
}
//公式15.19
for(l = 1; l <= n; l++)
{
for(i = 1; i <= n-l+1; i++)
{
j = i+l-1;
e[i][j] = 0x7fffffff;
//公式15.20
w[i][j] = w[i][j-1] + p[j] + q[j];
for(r = i; r <= j; r++)
{
//公式15.19
t = e[i][r-1] + e[r+1][j] + w[i][j];
//取最小值
if(t < e[i][j])
{
e[i][j] = t;
//记录根结点
root[i][j] = r;
}
}
}
}
}
/********练习********************************************/
//15.5-1输出最优二叉查找树
void Construct_Optimal_Best(int start, int end)
{
//找到根结点
int r = root[start][end];
//如果左子树是叶子
if(r-1 < start)
cout<<'d'<<r-1<<" is k"<<r<<"'s left child"<<endl;
//如果左子树不是叶子
else
{
cout<<'k'<<root[start][r-1]<<" is k"<<r<<"'s left child"<<endl;
//对左子树递归使用Construct_Optimal_Best
Construct_Optimal_Best(start, r-1);
}
//如果右子树是叶子
if(end < r+1)
cout<<'d'<<end<<" is k"<<r<<"'s right child"<<endl;
//如果右子树不是叶子
else
{
cout<<'k'<<root[r+1][end]<<" is k"<<r<<"'s right child"<<endl;
//对右子树递归使用Construct_Optimal_Best
Construct_Optimal_Best(r+1, end);
}
}
int main()
{
int n = N;
// double p[N+1] = {0, 0.15, 0.10, 0.05, 0.10, 0.20};
// double q[N+1] = {0.05, 0.10, 0.05, 0.05, 0.05, 0.10};
double p[N+1] = {0, 0.04, 0.06, 0.08, 0.02, 0.10, 0.12, 0.14};
double q[N+1] = {0.06, 0.06, 0.06, 0.06, 0.05, 0.05, 0.05};
Optimal_Bst(p, q, n);
// PrintE();
// PrintW();
// PrintRoot();
cout<<'k'<<root[1][N]<<" is root"<<endl;
Construct_Optimal_Best(1, N);
return 0;
}