深入Java集合系列之五：PriorityQueue

前言

今天继续来分析一下PriorityQueue的源码实现，实际上在Java集合框架中，还有ArrayDeque（一种双端队列），这里就来分析一下PriorityQueue的源码。PriorityQueue也叫优先队列，所谓优先队列指的就是每次从优先队列中取出来的元素要么是最大值（最大堆），要么是最小值（最小堆）。我们知道，队列是一种先进先出的数据结构，每次从队头出队（移走一个元素），从队尾插入一个元素（入队），可以类比生活中排队的例子就好理解了。

PriorityQueue说明

PriorityQueue底层实现的数据结构是“堆”，堆具有以下两个性质：

任意一个节点的值总是不大于（最大堆）或者不小于（最小堆）其父节点的值；堆是一棵完全二叉树

而优先队列在Java中的使用的最小堆，意味着每次从队列取出的都是最小的元素，为了更好理解源码，有必要了解堆的一些数字规律。我们知道无论堆还是其他数据结构，最终都要采用编程语言加以实现，在Java中实现堆这种数据结构归根结底采用的还是数组，但这个数组有点特殊，每个数组中的元素的左右孩子节点也存在该数组中，对于任意一个数组下标i，满足：

左孩子节点的下标left(i)=2*i，右孩子节点right(i) = 2*i+1

这样的话就可以把数据结构中复杂的树形元素放在简单的数组中了，只要按照上面的规律就可以很方便找到任意节点的左右孩子节点。解决完元素的存储问题还要把数组中的元素还原为堆，这就是建堆的过程，后面的源码也是基于同样的思想。以每次向堆中添加一个元素为例，由于使用数组存储，新添加的元素的下标是数组的最后一个下标值，对应到堆中就是堆中最后一个叶子节点，由于新添加元素破坏了堆的性质，所以需要对新的添加的元素做调整，使其移动到正确的位置，使得堆重新符合堆的性质。

那么问题来了，从哪个位置开始建堆呢？我们注意到最后一个节点的父节点是拥有孩子节点的下标最大的节点，因为叶子节点没有孩子节点，基于这点考虑我们选择最后一个节点的父节点作为建堆的起点，对与每个节点来说，接着要做的就是调整节点的位置了，这是实现最大堆或者最小堆的关键，为了能形象说明建堆的过程，请参看下面的示意图：

下面以元素｛6，5，3，1，4，8，7｝为例，说明建堆的具体过程：

如果你觉得这个过程太单调，你可以参考下面的动态图，不过下面这个动态图还包括堆排序的内容，只需要关注前面建堆哪个动态图就好了。

好了，现在你应该了解了建堆的具体过程，下面的关键就是添加元素以及移除元素了，为了结合Priority的源码说明，我把这部分的内容留到源码分析了。

源码分析

入队

在分析入队之前，我们来看看Java源码是怎么建堆的？

//从插入最后一个元素的父节点位置开始建堆
private void heapify() {
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        siftDown(i, (E) queue[i]);
}
//在位置k插入元素x，为了保持最小堆的性质会不断调整节点位置
private void siftDown(int k, E x) {
    if (comparator != null)
        //使用插入元素的实现的比较器调整节点位置
        siftDownUsingComparator(k, x);
    else
        //使用默认的比较器（按照自然排序规则）调整节点的位置
        siftDownComparable(k, x);
}
//具体实现调整节点位置的函数
private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>)x;
    // 计算非叶子节点元素的最大位置
    int half = size >>> 1;        // loop while a non-leaf
    //如果不是叶子节点则一直循环
    while (k < half) {
        //得到k位置节点左孩子节点，假设左孩子比右孩子更小
        int child = (k << 1) + 1; // assume left child is least
        //保存左孩子节点值
        Object c = queue[child];
        //右孩子节点的位置
        int right = child + 1;
        //把左右孩子中的较小值保存在变量c中
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        //如果要插入的节点值比其父节点更小，则交换两个节点的值
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    //循环结束，k是叶子节点
    queue[k] = key;
}

ok，下面看看如何在一个最小堆中添加一个元素：

public boolean add(E e) {
    //调用offer函数
    return offer(e);
}
//siftUp之前的代码主要确认队列的容量不发生溢出，并保存队列中的元素个数以及发生结构//性修改的次数
public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);
    size = i + 1;
    if (i == 0)
        queue[0] = e;
    else
        //具体执行添加元素的函数
        siftUp(i, e);
    return true;
}
//调用不同的比较器调整元素的位置
private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}
//使用默认的比较器调整元素的位置
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        //保存父节点的值
        Object e = queue[parent];
        //使用compareTo方法，如果要插入的元素小于父节点的位置则交换两个节点的位置
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}
//调用实现的比较器进行元素位置的调整，总的过程和上面一致，就是比较的方法不同
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        //这里是compare方法
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

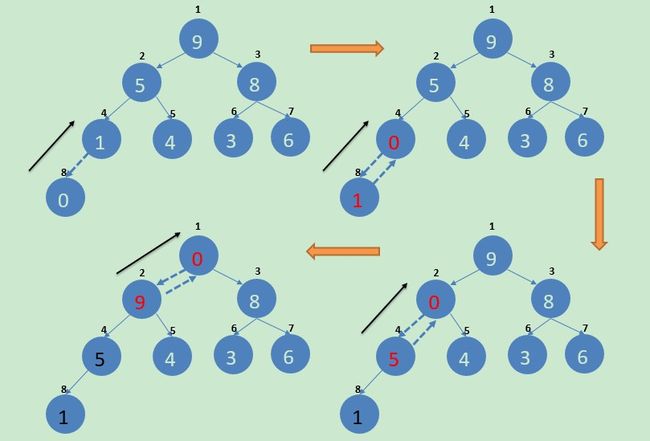
为了更好理解上面代码的执行过程，请参看下面的示意图：

出队

出队就是从队列中移除一个元素，我们看看在源码中实现：

private E removeAt(int i) {
    assert i >= 0 && i < size;
    modCount++;
    //s是队列的队头，对应到数组中就是最后一个元素
    int s = --size;
    //如果要移除的位置是最后一个位置，则把最后一个元素设为null
    if (s == i) // removed last element
        queue[i] = null;
    else {
        //保存待删除的节点元素
        E moved = (E) queue[s];
        queue[s] = null;
        //先把最后一个元素和i位置的元素交换，之后执行下调方法
        siftDown(i, moved);
        //如果执行下调方法后位置没变，说明该元素是该子树的最小元素，需要执行上调方//法,保持最小堆的性质
        if (queue[i] == moved) {//位置没变
            siftUp(i, moved);   //执行上调方法
            if (queue[i] != moved)//如果上调后i位置发生改变则返回该元素
                return moved;
        }
    }
    return null;
}

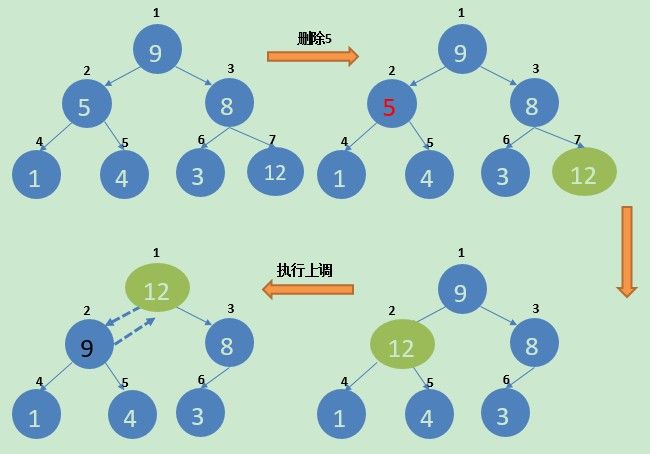
在上面的代码上调方法与下调方法只会执行其中的一个，参看下面需要执行下调方法的示意图：

这是需要执行上调方法的示意图：

PriorityQueue小结

经过上面的源码的分析，对PriorityQueue的总结如下：

• 时间复杂度：remove()方法和add()方法时间复杂度为O(logn)，remove(Object obj)和contains()方法需要O(n)时间复杂度，取队头则需要O(1)时间
• 在初始化阶段会执行建堆函数，最终建立的是最小堆，每次出队和入队操作不能保证队列元素的有序性，只能保证队头元素和新插入元素的有序性，如果需要有序输出队列中的元素，则只要调用Arrays.sort()方法即可
• 可以使用Iterator的迭代器方法输出队列中元素
• PriorityQueue是非同步的，要实现同步需要调用java.util.concurrent包下的PriorityBlockingQueue类来实现同步
• 在队列中不允许使用null元素