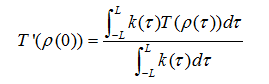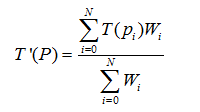基于LIC算法的二维矢量场可视化
线积分卷积算法(Line Integral Convolution,LIC法)是一种经典的矢量场可视化方法,由Cabral和Leedom 在1993年的SIGGRAPH大会上提出,该算法可以有效地表征二维矢量场,既能清楚直观地反映出每点的速度方向,又能表达矢量场的细节。该算法的提出对于矢量场可视化具有广泛而深远的意义,已被成功应用到很多领域。其发展至今,已经涉及到噪声选取、信号滤波、卷积运算、纹理映射及计算机动画等多种技术,具有广阔的发展前景。
用卷积来表示矢量场的方向源于一种运动模糊的思想。LIC算法原理可概述为利用一维低通卷积核双向对称地沿流线方向卷积白噪声纹理,最终合成矢量纹理。下图为LIC算法计算示意图。
离散形式为:
其中,T为输入白噪声纹理,T(ρ(τ))为流线上各点噪声纹理值。k(τ)为卷积核(可为盒型卷积核、三角卷积核等),表示流线各点与P的相关性。pi为流线上的N个离散点,Wi为pi对P的贡献,即卷积核k(τ)在点pi-1和pi之间覆盖的面积。原始的LIC算法计算效率较差,Stalling和Hege在1995年的SIGGRAPH会议上提出了FastLIC算法,从计算速度和图像分辨率等方面对LIC算法进行了改进。该算法考虑盒型卷积核作用下,利用同一条流线上相邻像素之间的相关性,构造出差分表达式:
在一次积分过程中计算出多个像素值,从而去掉了很多重复计算,使计算的线积分数量大为减少,提高了LIC算法的计算速度,并通过四阶Runge-Kutta数值积分法改进了LIC算法的精度。下图为通过LIC算法生成的矢量纹理,第一行为模拟矢量场数据,第二行为数值预报风场数据。