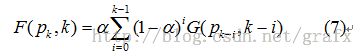基于IBFV算法的二维矢量场可视化

       1. IBFV算法简介

        IBFV (Image Based Flow Visualization) 算法于2002年SIGGRAPH大会上由van Wijk首次提出。该算法基于图像平流思想，最终流场动画的每一帧都是由之前图像和一系列经过滤波的噪声背景图像卷积得到，是一种用宏观图形表现微观粒子运动的方法。相比点噪声算法、LIC算法，IBFV算法可以充分利用计算机图形硬件的图像混合及纹理映射功能，将大部分复杂的显示计算过程交由图形硬件来完成，从而整体获得较高的绘制速度。基于IBFV算法的扩展性研究很多，van Wijk将IBFV算法成功应用于曲面流场的可视化，该算法以三角网格为基本图元，首先将3D曲面投影到2D平面，然后进行纹理平流与混合，最终实现曲面流场的运动。Telea与van Wijk提出了基于硬件加速的3D IBFV算法，将IBFV算法拓展到3D空间，该算法采用一种纹理平流技术，通过向前的纹理平流与原有的纹理进行比例混合，实现流场中粒子的运动。文献4应用IBFV算法对空间晶体生长实验中产生的流场数据进行可视化，实现了流场数据的实时动态显示。

       2. IBFV算法数学描述

       对于给定的二维稳定矢量场，

                                                                   

       其中 p∈S 为空间位置点集， v(p) 为相应位置处的速度， S 为矢量场的定义域。对于该矢量场中的任意质点，它的运动方程满足：

                                                                                    

       一阶欧拉近似解为：

                                                                              

       其中 k∈N ，为流场动画的帧数。

       假定 F(p, k) 为流场动画帧，采用矢量场定义域 S 对 F 进行网格划分，并将每一个网格单元 F(p_k, k) 看作质点按公式(3)进行图像平流，设 F(p_k+1, k+1) 为平流后的网格单元。对于二维稳定场平流轨迹将为流线，则 F 沿矢量场平流的过程可近似为：

                                                                

       由方程(4)可知，若 p_k 平流出流场定义域 S ，则这样 F 将被平流为全黑（值全为0）的图像。为了避免这种情况发生，在每次平流过程中，增加背景噪声图像 G 的影响，则有下面方程：

                                                        

       其中 α∈ [0, 1] 为混合参数，方程(5)递推可得方程(6) ：

                                                   

       在方程(6)中，第一项代表初始图像对结果的影响，当初始图像为全黑图像（即 F(p_k, k) = 0 ）或者 k 值取很大时，第一项可以忽略不计。由此可得方程 (7) ：

                                                                   

       该式表明，图像中点 p_k 的颜色值可由图列 G(p,i) 沿着通过 p_k 的流线积分卷积得出，卷积核为 α •   (1 − α)ⁱ ，即将现有图像沿流场方向平流，然后与背景图像相融合得出新的图像，重复这个迭代过程，将得到矢量场的动态描述。一般情况下，卷积长度为32时，即可获得稳定的矢量场动画，卷积长度也可称为图像平流周期。

       该算法实现的关键是合理地选取混合参数 α 和背景图像 G 。在实际应用当中 α 将被初始化为常数， α 值越大，背景图像 G 的影响将增加，矢量线间对比度将会提高，但矢量场的方向性将会被减弱。对于背景图像 G ，如果平流过程中始终不变，则最终平流的结果图像将是静态的，不能表现出矢量场动态的效果。因此每次平流都必须有不同的背景图像 G ，van Wijk通过研究认为，通过方波信号滤波并且相位变化的白噪声纹理将是合适的选取对象，即准备 M 幅不同的背景图像循环使用，这样就可以得到矢量场的动态显示。背景图像 G 中 p  点的颜色值可由下式计算得出：

                                              

上式中 k 为平流帧数， M 为图像平流周期， Noise 为白噪声纹理。

       通过分析公式(7)及(8)，并与LIC算法进行对比，我们可以得出通过该算法获得的结果图像对比度低的主要原因，即参与卷积的每一项 G(p_k−i, k − i) 的灰度值，并不像LIC算法那样来自同一幅白噪声纹理，而是来自一个变化的多幅背景噪声纹理，因此矢量方向相关性被降低，导致纹理细节不清晰。

       3. IBFV算法计算步骤

                                             

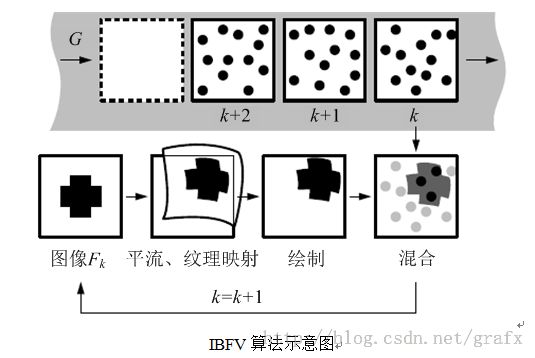
       IBFV 算法以纹理动画的形式对当前矢量场进行可视化，上图为IBFV算法计算示意图，其计算步骤如下：

       (1) 首先初始化相关参数，其中主要影响绘制质量的参数为图像混合参数 α ，取值区间为0.0~1.0，一般合理的取值范围为0.05~0.15；然后读取矢量数据；最后生成 M 幅噪声背景图像，背景图像记为 G ，背景图像大小一般以64×64为适宜，当然也可以选取其他分辨率；

       (2) 对于当前第 k 帧图像 F_k ，首先将网格单元沿矢量场方向平流，计算网格单元每个顶点平流位置，然后进行网格单元纹理映射，即将原网格单元内的图像映射到新网格单元；

       (3) 绘制平流后的图像 F_k ；

       (4) 将当前图像 F_k 与背景图像 G_k 混合，获得图像 F_k+1 ；

       (5) 注入染料；

       (6) 保存当前图像 F_k+1 至帧缓存。

       执行完步骤(1)后，以 M 为周期，重复执行步骤(2)至(6)，将得到动态的矢量场显示，当 k=M 时取 k=1 ，开始新一轮的循环绘制。上面步骤中，步骤(5)注入染料模拟了传统实验型矢量场可视化技术当中的添加外部介质方法，通过观察染料的扩散方向可以准确的判断矢量场的运动方向以及运动变化细节，该步骤为可选步骤。

       4. IBFV算法绘制结果与分析

       下图为截取的 IBFV 算法矢量动画单帧效果图， 数据为 模拟涡流场数据，数据大小为 100 × 100 。使用普通PC机，算法基于 VC 6.0 环境调用 OpenGL 函数库实现，显示窗口大小为 400 × 400 ，图像平流周期 M 为 32 ，混合参数 α 为 0.1 ，绘制速度大于 50 帧 / 秒。

                                            

                                            

       前三幅图 为矢量场直接绘制结果，最后一幅图 为在矢量场中注入染料之后的绘制结果，根据染料的扩散方向，可以清晰的观察到中间涡流点附近流场的流动方向及流动时流场内部相互作用情况。相比点噪声算法、 LIC算 法，该算法单帧图像空间一致性不高，矢量线间对比度低，纹理细节不清晰，但该算法充分利用了计算机图形硬件的纹理映射和图像混合功能，获得的高速矢量场动画可以很好的表征矢量场的运动方向及细节变化，在这一点上远远优于其他两种方法，因此具有较高的实用价值。

参考文献：

1  Jarke J. van Wijk. Image based flow visualization[A]. In: Proceedings of ACM SIGGRAPH 2002[C], San Antonio, Texas, United States, 2002 : 745 - 754.

2  Jarke J. van Wijk. Image based flow visualization for Curved Surfaces. In: Proceedings of IEEE Visualization 2003[C], Seattle, Washington, 2003:123-130.

3  Alexandru Telea, Jarke J. van Wijk. 3D IBFV:hardware - accelerated 3D flow visualization[A]. In: Proceedings of IEEE Visualization 2003[C], seattle,

4 吴晓莉,史美萍,贺汉根.空间晶体生长实验中流场的动态显示研究[J].计算机仿真，2007，24(4)：190-192.