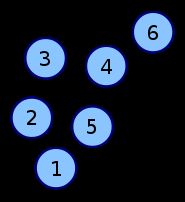
图的基本操作(基于邻接矩阵):图的构造,深搜(DFS),广搜(BFS)
Adjacency Matrix
邻接矩阵是表示一个图的常用存储表示。它用两个数组分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。阶为n的图G的邻接矩阵A是n*n的。将G的顶点标签为v_1,v_2,...,v_n。若(v_i,v_j) \in E(G),A_{ij}=1,否则A_{ij}=0。
Depth-First-Search
是沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所有边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
搜索结果:1 2 3 4 5 6 7 8 9 10 11 12
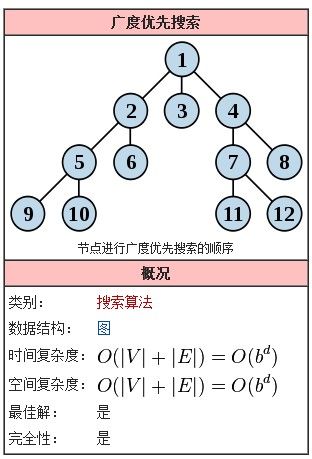
Breadth-First-Search
简称BFS,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
搜索结果:1 2 3 4 5 6 7 8 9 10 11 12
Implementation
#include <iostream>
#include <string>
#include <queue>
using namespace std;
#define MAXN 100
struct Graph
{
string vertex[MAXN];
int matrix[MAXN][MAXN];
int vertexNum;
int arcNum;
};
int Locate(Graph g,string str)
{
for(int i =0;i<g.vertexNum;i++)
{
if(str == g.vertex[i])
return i;
}
return -1;
}
void CreateDUG(Graph &g) //构造无向图
{
string start,end;
cout << "请输入顶点和边数:"<<endl;
cin>>g.vertexNum>>g.arcNum;
for(int i = 0;i<g.vertexNum;i++)
{
cout<<"请输入第"<<i<<"个顶点:"<<endl;
cin>>g.vertex[i];
}
for(int i = 0;i<g.vertexNum;i++)
{
for(int j = 0;j<g.vertexNum;j++)
{
g.matrix[i][j] = 0;
}
}
for(int i = 0;i <g.arcNum;i++)
{
cout<<"请输入第"<<i<<"条边的起始和结束顶点"<<endl;
cin>>start>>end;
int m = Locate(g,start);
int n = Locate(g,end);
g.matrix[m][n] = 1;
g.matrix[n][m] = 1;
}
}
void CreateUDN(Graph &g) //构造无网
{
string start,end;
int w;
cout << "请输入顶点和边数:"<<endl;
cin>>g.vertexNum>>g.arcNum;
for(int i = 0;i<g.vertexNum;i++)
{
cout<<"请输入第"<<i<<"个顶点:"<<endl;
cin>>g.vertex[i];
}
for(int i = 0;i<g.vertexNum;i++)
{
for(int j = 0;j<g.vertexNum;j++)
{
g.matrix[i][j] = 0;
}
}
for(int i = 0;i <g.arcNum;i++)
{
cout<<"请输入第"<<i<<"条边的起始和结束顶点和权"<<endl;
cin>>start>>end>>w;
int m = Locate(g,start);
int n = Locate(g,end);
g.matrix[m][n] = w;
g.matrix[n][m] = w;
}
}
void CreateDG(Graph &g) //构造有向图
{
string start,end;
cout << "请输入顶点和边数:"<<endl;
cin>>g.vertexNum>>g.arcNum;
for(int i = 0;i<g.vertexNum;i++)
{
cout<<"请输入第"<<i<<"个顶点:"<<endl;
cin>>g.vertex[i];
}
for(int i = 0;i<g.vertexNum;i++)
{
for(int j = 0;j<g.vertexNum;j++)
{
g.matrix[i][j] = 0;
}
}
for(int i = 0;i <g.arcNum;i++)
{
cout<<"请输入第"<<i<<"条边的起始和结束顶点"<<endl;
cin>>start>>end;
int m = Locate(g,start);
int n = Locate(g,end);
g.matrix[m][n] = 1;
}
}
void CreateDN(Graph &g) //构造有向网
{
string start,end;
int w;
cout << "请输入顶点和边数:"<<endl;
cin>>g.vertexNum>>g.arcNum;
for(int i = 0;i<g.vertexNum;i++)
{
cout<<"请输入第"<<i<<"个顶点:"<<endl;
cin>>g.vertex[i];
}
for(int i = 0;i<g.vertexNum;i++)
{
for(int j = 0;j<g.vertexNum;j++)
{
g.matrix[i][j] = 0;
}
}
for(int i = 0;i <g.arcNum;i++)
{
cout<<"请输入第"<<i<<"条边的起始和结束顶点和权"<<endl;
cin>>start>>end>>w;
int m = Locate(g,start);
int n = Locate(g,end);
g.matrix[m][n] = w;
}
}
int FirstAdjVex(Graph g,int v)//返回v的第一个邻接顶点序号
{
for(int i = 0;i<g.vertexNum;i++)
{
if(g.matrix[v][i] == 1)
return i;
}
return -1;
}
int NextAdjVex(Graph g,int v,int w)//返回顶点v相对于w的下一个邻接点序号
{
for(int i = w+1;i<g.vertexNum;i++)
{
if(g.matrix[v][i] == 1)
return i;
}
return -1;
}
bool visted[MAXN];
void DFS(Graph g,int i)
{
cout <<g.vertex[i]<<" ";
visted[i] = true;
for(int w = FirstAdjVex(g,i);w>=0;w = NextAdjVex(g,i,w))
{
if(!visted[i])
DFS(g,w);
}
}
void DFSTransfer(Graph g)
{
for(int i =0;i<g.vertexNum;i++)
{
visted[i] = false;
}
for(int i = 0;i<g.vertexNum;i++)
{
if(!visted[i])
DFS(g,i);
}
cout << endl;
}
void BFS(Graph g,int v)
{
}
void BFSTransfer(Graph g)
{
for(int i =0;i<g.vertexNum;i++)
{
visted[i] = false;
}
std::queue<int> que;
for(int i = 0;i<g.vertexNum;i++)
{
if(!visted[i])
{
que.push(i);
visted[i] = true;
while(!que.empty())
{
int k = que.front();
que.pop();
cout <<g.vertex[k]<<" ";
for(int i = FirstAdjVex(g,k);i>=0;i = NextAdjVex(g,k,i))
{
if(!visted[i])
{
que.push(i);
visted[i] = true;
}
}
}
}
}
cout <<endl;
}
int main()
{
Graph g;
CreateDUG(g);
DFSTransfer(g);
BFSTransfer(g);
return 0;
}
Reference
- 《算法导论》 第22章 图的基本算法P322
- http://en.wikipedia.org/wiki/Breadth-first_search
- http://en.wikipedia.org/wiki/Depth-first_search