Z-Buffer 与 W-Buffer
w 的含义
3D空间点的坐标是(x,y,z),为了使矩阵乘法具有平移变换的功效,我们用4D空间中的点(x,y,z,w)来表示3D空间中的点(x',y',z'),这两个不同空间点之间的关系是:
x' = x / w
y' = y / w
z' = z / w
像这样用四维空间点表示三维空间点,或者说用 n + 1 维空间点表示 n 维空间点的方法叫做 “齐次坐标表示法”。
实际使用中,在模型->世界转换、世界->视图转换过程中,w 通常保持不变,总是等于一,这样,齐次坐标的前三个分量就是对应3D空间点的三个坐标分量。但是,经过投影变换后,w 将得到一个比例值,比如,一般的透视投影变换矩阵是:
| W 0 0 0 |
| 0 H 0 0 |
| 0 0 Q 1 |
| 0 0 -QZn 0 |
其中 Zn = 近裁剪面 z 坐标
Zf = 远裁剪面 z 坐标
W = 2 * Zn / 视口宽度
H = 2 * Zn / 视口高度
Q = Zf / (Zf - Zn)
将点(x,y,z,1)乘以此矩阵,w 便不再是一,而对应的3D空间点坐标(x / w,y / w,z / w)
将出现一个缩放效果。同时,因为 w 的值通常与 z 坐标成正比(比如经过上面这个矩阵的变换,w 的值其实就是 z 坐标的值),
所以经过投影变换,物体会产生近大远小的效果。
Z-Buffer 与 W-Buffer 的区别
简单的说,z-buffer 与 w-buffer 的区别就是前者保存的是点的 z 坐标,而后者保存的是点的 w 坐标。
具体的说,两者因为保存的值有不同的含义,所以表现出来的实际效果也会有差别。
z-buffer 保存的是经过投影变换后的 z 坐标,前面说过,投影后物体会产生近大远小的效果,所以距离眼睛比较近的地方,z 坐标的分辨率比较大,而远处的分辨率则比较小,换句话说,投影后的 z 坐标在其值域上,对于离开眼睛的物理距离变化来说,不是线性变化的(即非均匀分布),这样的一个好处是近处的物体得到了较高的深度分辨率,但是远处物体的深度判断可能会出错。
w-buffer 保存的是经过投影变换后的 w 坐标,而 w 坐标通常跟世界坐标系中的 z 坐标成正比,所以变换到投影空间中之后,其值依然是线性分布的,这样无论远处还是近处的物体,都有相同的深度分辨率,这是它的优点,当然,缺点就是不能用较高的深度分辨率来表现近处的物体。
从硬件实现角度来说,几乎所有的硬件3D加速卡都支持 z-buffer,而 w-buffer 的支持没有 z-buffer 那么广泛。另外,早期的 Direct3D 版本看起来也不支持 w-buffer。
Z-Buffer 与 W-Buffer 之间的转换
根据上面的矩阵变换,可以很容易的导出将 w-buffer 转换成 z-buffer 的公式:
zDepth = Q * ( wDepth - Zn ) / wDepth
= Zf / ( Zf - Zn ) * ( wDepth - Zn ) / wDepth
这个转换公式有什么用处?举个例子:3DS MAX 使用的是 w-buffer,如果从 3DS MAX 中导出深度信息到 Direct3D 中,作为预渲染的背景使用,就有可能用到上面这个转换。当然,如果在 D3D 中使用 w-buffer,问题就不大了,但是如果使用 z-buffer,不经过这样的转换,渲染结果就会出错。
文档内容:
[Part 1]
幾乎所有目前的 3D 顯示晶片都有 Z buffer 或 W buffer。不過,還是常常可以看到有人對 Z buffer 和 W buffer 有一些基本的問題,像是 Z buffer 的用途、Z buffer 和 W buffer 的差別、或是一些精確度上的問題等等。這篇文章的目的就是要簡單介紹一下 Z buffer 和 W buffer。
Z buffer 和 W buffer 是做什麼用的呢?它們的主要目的,就是去除隱藏面,也就是 Hidden surface elimination(或是找出可見面,Visible surface detemination,這是同樣意思)。在 3D 繪圖中,只要有兩個以上的三角面,就可能會出現某個三角面會遮住另一個三角面的情形。這是很明顯的現象,因為近的東西總是會遮住遠的(假設這些三角面都是不透明的)。所以,在繪製 3D 場景時,要畫出正確的結果,就一定要處理這個問題。
不過,這個問題是相當困難的,因為它牽扯到三角面之間的關係,而不只是某個三角面本身而已。所以,在做去除隱藏面的動作時,是需要考慮場景中所有的三角面的。這讓問題變得相當的複雜。而且,三角面往往並不是整個被遮住,而常常是只有一部分被遮住。所以,這讓問題變得更複雜。
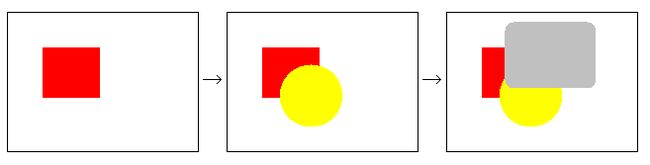
要做到去除隱藏面的最簡單方法,就是「畫家演算法」(Painter's algorithm)。這個方法的原理非常簡單,也就是先畫遠的東西,再畫近的東西。這樣一來,近的東西自然就會蓋住遠的東西了。因為油畫的畫家通常會用這樣的方法,所以這個方法被稱為「畫家演算法」。下圖是一個例子:
上圖中,紅色的圓形最遠,所以最先畫。然後是黃色的三角形,最後是灰色的方形。照遠近的順序來畫,就可以達到去除隱藏面的效果。所以,只要把 3D 場景中的三角面,以對觀察者的距離遠近排序,再從遠的三角面開始畫,應該就可以畫出正確的結果了。
不過,實際上並沒有這麼理想。在 3D 場景中,一個三角面可能有些地方遠,有些地方近,因為三角面有三個頂點,而這三個頂點和觀察者的距離,通常都是不同的。所以,要以哪個頂點來排序呢?或是以三角面的中心來排序?事實上,不管以什麼為依據來排序,都可能會有問題。下圖是一個「畫家演算法」無法解決的情形:
上圖中,三個三角面互相遮住對方,所以不管用什麼順序去畫,都無法得到正確的結果。另外,這個方法也無法處理三角面有交叉的情形。
當然,如果相當確定場景中不會出現這麼奇怪的情形,那「畫家演算法」一般還是可以用的。不過,它還有一個很大的問題,就是效率不佳。首先,畫家演算法需要對場景中,在視角範圍內所有的三角面做一個排序的動作。最好的排序演算法也需要 O(n log n) 的時間。也就是說,(大致上來說)如果三角面的數目從一千個變一萬個,排序需要的時間會變成約 13.3 倍。而且,因為這需要對場景中所有的三角面來做,因此也不適合用特別的硬體來做加速。另外,這個方法還有一個很大的問題,就是它會花很多時間去畫一些根本就會被遮住的部分,因為每個三角面的每個 pixel 都需要畫出來。這也會讓效率變差。
如果場景是靜態(不動)的,只有觀察者會變動的話,那是有方法可以加快排序的速度。一個很常用的方法是 binary space paritioning(BSP)。這個方法需要事先對場景建立一個樹狀結構。建立這個結構後,不管觀察者的位置、角度是如何,都可以很快找出正確的繪製順序。而且,BSP 會視需要切開三角面,以處理像上圖那樣,三個三角面互相遮住對方的情形。
不過,BSP 結構在建立時,要花很多時間,所以不太可能即時運算。因此,通常只能用在場景中的靜態部分,而會動的部分還是需要另外排序。而且,BSP 常會需要切開三角面,也會讓三角面的數目增加。另外,BSP 仍然無法解決需要畫出那些被遮住的 pixel 的問題。
另一種去除隱藏面的方法,是直接以 pixel 為單位,而不是以三角面為單位,來考慮這個問題。其中最簡單的方法是由 Catmull 在 1974 年時提出來的,也就是 Z buffer(或稱 depth buffer)。這個方法非常簡單,又容易由特別設計的硬體來執行,所以在記憶體容量不再是問題後,就變得非常受歡迎。
Z buffer 的原理非常簡單。在繪製 3D 場景時,除了存放繪製結果的 frame buffer 外,另外再使用一個額外的空間,也就是 Z buffer。Z buffer 記錄 frame buffer 上,每個 pixel 和觀察者的距離,也就是 Z 值。在開始繪製場景前,先把 Z buffer 中所有的值先設定成無限遠。然後,在繪製三角面時,對三角面的每個 pixel 計算該 pixel 的 Z 值,並和 Z buffer 中存放的 Z 值相比較。如果 Z buffer 中的 Z 值較大,就表示目前要畫的 pixel 是比較近的,所以應該要畫上去,並同時更新 Z buffer 中的 Z 值。如果 Z buffer 中的 Z 值較小,那就表示目前要畫的 pixel 是比較遠的,會被目前 frame buffer 中的 pixel 遮住,所以就不需要畫,也不用更新 Z 值。這樣一來,就可以用任意的順序去畫這些三角面,即可得到正確的繪製結果。下圖是一個例子:
上圖中,紅色的三角面雖然先畫出來,但是因為使用了 Z buffer,所以後畫的黃色方塊還是只會遮住適當的部分,而不會連較近的部分都遮住。這就顯示出 Z buffer 的效果。
實際上 Z buffer 中能存放的數字當然會有一定的限度,所以通常會把 Z 值縮小到 0 ~ 1 的範圍。因此,在繪製 3D 場景時,就會需要把可能出現的 Z 值限制在某個範圍內。通常是用兩個和投影平面平行的平面,把所有超出這兩個平面範圍的三角面都切掉。這兩個平面通常分別稱為 Z near 和 Z far,分別表示較近的平面和較遠的平面。而在 Z near 平面的 Z 值為 0,在 Z far 的 Z 值為 1。
在效率上 Z buffer 並不一定會比「畫家演算法」要快。但是,它比較簡單。而且,它的效率和三角面的數目並沒有太大的關係,而是和繪製的 pixel 數目有關。所以,而且可以很容易設計出特定的 3D 硬體來做這個動作,而不需要由 CPU 來做。而 Z buffer 所需要的額外記憶體,在今天已經顯得不是很重要。所以現在幾乎所有的 3D 顯示晶片都是使用 Z buffer。
不過,Z buffer 並非全無問題。一個很大的問題是在於精確度上。如果有兩個三角面很靠近,而其中一個完全在另一個之前,那應該只能看到一個三角面才對。但是,如果 Z buffer 的精確度不夠,那這兩個三角面每個 pixel 的 Z 值可能會很接近。再加上計算出來的 Z 值一定會有誤差,所以,很可能會造成應該被遮住的三角面,卻有一些 pixel 沒有被遮住。這種情形稱為 Z fighting。下圖中,球在地面上的影子就是一個例子:
要避免這類問題,就要避免在場景中出現太過靠近,且接近平行的三角面。一般的場景不太會出現這個情形。不過,Z buffer 的精確度問題並不只是這樣而已。在下一部分會對這個問題有更詳細的說明。
[Part 2]
前面把 Z buffer 的原理做了一個大概的說明,聽起來 Z buffer 似乎是個很理想的技術。但是,實際上 Z buffer 有一個很大的問題,就是精確度的問題。
在前一頁後面所提到的,兩個非常接近的平面所出現的 Z fighting 情形,其實是相當少見,而且很容易避免的。當然,遇而還是會看到有一些遊戲會出現這種情形。不過,Z buffer 最嚴重的問題是在離觀察者較遠的部分。如果 Z buffer 的精確度不夠,而場景又很遠的的話,那遠處的東西就會出現一些非常奇怪的現象。下圖是一個例子:
 |
 |
| Z aliasing | 無 Z aliasing |
當然,上面的例子是比較極端的情形。實際上一般情形下並不會有這麼誇張的 Z aliasing 現象。不過,我相信大家多少都在一些場景較大的遊戲中,看過類似的情形。
為什麼會有這樣的現象呢?這就要從 Z buffer 的結構談起了。如果前一頁所說的,一般的顯示晶片,是把 Z 值限制在 0 ~ 1 的範圍,再用一個定點數去表示它。例如,一個 16 位元的 Z buffer,可能會用 0 ~ 65535(一個 16 位元數字可表示的範圍)來表示這個 0 ~ 1 之間的 Z 值。
如果 Z buffer 的分布在 eye space 中是線性的,也就是它的每個數字之間的間隔都相等的話,那這樣的精確度應該是蠻高的才對。因為,假設觀察者可以看到一公里遠的東西,那每個間隔就是約 1.5 公分。如果用更高精確度的數字來表示的話(像是 24 位元數字),那精確度還會更高。然而,Z buffer 在 eye space 中並不是線性的。它是在 projection space 中為線性。
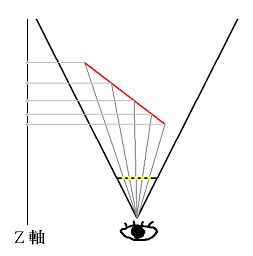
如果你覺得這些聽起來像是外星話的話,現在就要來「翻譯」這些外星話。首先,先來看一張示意圖:
上圖是一個眼睛在透視投影的情形下,觀看場景中的一個紅色平面的情形。靠近眼睛的平面(上面有黃色點的)是代表投影平面,也就是 3D 繪圖中的螢幕。黃色的點紅色平面投影到螢幕上的 pixel,他們當然是等間距的。但是,注意看這些「等間距」的 pixel,他們所對映的 Z 值(也就是 Z 軸上的那些灰色的點),並不是等間距的。實際上,離眼睛愈遠的 pixel,其 Z 軸上的間距就愈大。
這其實透視投影的一個明顯的性質。因為在透視投影的情形下,愈遠的東西看起來愈小,所以,在螢幕上同樣的間距,在比較遠的地方,就會變得比較大。因此,雖然三角面是平面,但是它在每個 pixel 上的 Z 值卻不是線性的變化。因此,就無法用線性內插來計算三角形內部的 pixel 的 Z 值。但是,要正確計算出每個 pixel 上的 Z 值,會需要一個除法的動作,而除法是很討厭、很花時間的動作。
早期的顯示晶片無法花費一個除法器在 Z buffer 上面。所以,一個方法是在 Z buffer 中,不要存放 eye space 的 Z 值,而改成存放 projection space 的 Z 值。這樣一來,Z 值在 projection space 就會變成是線性的,就可以簡單地用線性內插來計算三角形內部的 pixel 的 Z 值了。這也是目前幾乎所有顯示晶片的 Z buffer 的設計。
不過,在 projection space 中的 Z 值,就像上面的圖所顯示的一樣,有一個很重要的特性:它所對映的 eye space 的 Z 值間隔,在愈遠的地方就愈大。所以,Z buffer 的精確度,如果以 eye space 來看的話(這樣看才有意義),就會變成不平均的分布。離觀察者愈近的地方,其精確度會比遠的地方更高。而這個精確度的變化,會取決於 Z near 平面和 Z far 平面的位置。Z near 平面離觀察者愈近,且 Z far 平面離觀察者愈遠,則精確度的變化就會愈大,也就是遠的地方的精確度會愈差。
在這一頁最前面的兩張圖中,其 Z far 平面的位置是一樣的,但是左圖的 Z near 平面的位置,比右圖的 Z near 平面的位置近了一千倍。所以,在左圖中就出現了嚴重的 Z aliasing 現象,但是右圖就沒有出現這種現象。
所以,要儘可能避免 Z aliasing 現象,就要儘可能把 Z near 平面拉遠,而把 Z far 平面拉近。但是,實際上很多情形下,是無法允許這樣的設計的。比如說,在一個場景中,玩家可能會看到 50 公分遠的桌子上的東西,而同時看到窗外在一公里外的一座大基地。因此,Z near 平面不能設得比 50 公分要遠,但是 Z far 平面又得到一公里遠。以 16 位元 Z buffer 來看,那最遠處的間隔(也就是一公里遠的地方)會達到 30 公尺,也就是如果兩個 pixel 的間距小於 30 公尺的話,Z buffer 將無法分辨出正確的順序!而它在 Z near 處(也就是 50 公分的地方)的精確度則高達 0.0000076 公尺。這顯示出精確度分布是如此的不平均和不適當。如果改用 24 位元 Z buffer 的話,那情形會有相當程度的改善,在一公里遠處的精確度會提高到約 12 公分。這也是為什麼 24 位元 Z buffer 很少會顯示出 Z aliasing 的情形。
不過,即使是 24 位元 Z buffer 也不見得是完全理想。以上面的例子來說,如果 Z near 平面移到 10 公分處,在遠處的精確度就會從 12 公分降低為 60 公分。有些人可能會覺得,在一公里遠的地方,又有誰能分辨 60 公分,或是 12 公分呢?但是,問題在於,當兩個大的平面的距離小於 60 公分時,因為 Z buffer 無法分辨出正確的順序,就可能會在這一框是某個平面被畫出來,而在下一框卻變成是另一個平面被畫出來。如果這兩個平面的顏色差別很大,就會產生閃爍的現象,任何人都會很容易就注意到的。
有些顯示晶片採取一些方法來解決這個問題。一個簡單的想法是在 Z buffer 中使用浮點數,而不使用定點數。經過適當的設計,浮點數可以在某個特定的數字附近,提供更大的精確度範圍(一般情形是在 0 附近)。而一般的 Z buffer 在 Z far 附近會需要更高的精確度,所以可以把 Z buffer 在 Z far 平面以 0 表示,而 Z near 平面以 1 表示。這樣就可以得到更高的精確度。不過,浮點數在計算上比較麻煩。特別是 Z buffer 的運算中,常需要做加法和比較的運算,這都會比定點數的運算要麻煩很多。
另外一個方法是用非線性的 Z buffer。例如,可以把 Z buffer 切成很多個小區間,而每一個小區間中都是一般的線性 Z buffer。但是,可以在遠方分配更多的小區間,讓它的精確度可以提高。這也是一種解決精確度問題的方式。
其實,要解決 Z buffer 精確度問題,最簡單的方法就是在 eye space 中做線性內插。但是,前面已經說過,在 eye space 中的線性,在 projection space 並不一定是線性,所以它會需要額外的除法器。不過,有一個方法可以避免使用除法器,而只需要「倒數器」,「倒數器」比完整的除法器要簡單一些。這個方法就是先以較高的精確度,在 projection space 中,對 Z 做線性內插。對每個內插得到的結果,再用倒數器算出其倒數,也就是所謂的 W 值。這個 W 值的精確度可以較低,因為它在 eye space 中的分布是平均的。最後,再把這個 W 值和 "W buffer" 裡面的值做比較,就可以得到正確的順序。這個方法,相信有些人已經猜到了,就是W buffering。
當然,另外還有一些別的方法可以實作出 W buffer。不過,不管是用什麼方法實作 W buffer,其最重要的性質就是在 eye space 中為線性分布。因此,16 位元的 W buffer 在遠處的精確度是非常理想的。以前面的例子來說,即使是 24 位元 Z buffer,在一公里遠處的精確度也只能到 12 公分。但是 16 位元 W buffer 則是每個地方的精確度都是 1.5 公分。因此,在這個例子中,16 位元 W buffer 在遠處的表現,甚至比 24 位元 Z buffer 更好。
而且,W buffer 還有一個好處,就是其 W near 平面(相對於 Z buffer 中的 Z near 平面)的位置是不重要的。也就是說,W buffer 可以同時兼顧眼前的桌子,和數公里外的巨大基地。而用 Z buffer 的話,如果想要能正確顯示出數公里外的巨大基地,那可能就得犧牲眼前的桌子了。
不過,因為 W buffer 的精確度是平均分布,它在 Z near 處的精確度就明顯不如 Z buffer 了。雖然說 Z buffer 在 Z near 處的精確度是過於高了(像是 0.0000076 公尺),但是,W buffer 卻可能會過於低。比如說,1.5 公分的精確度對於遠處的物體是絕對足夠的,但是對於靠近觀察者的物體,則是明顯的不足。比如說,桌上可能有一本厚度小於 1.5 公分的書。這時,1.5 公分的精確度是完全不夠的。
這樣聽起來,好像 W buffer 也無法解決問題嘛!其實並不是這樣的。如果有 24 位元的 W buffer,同時可以看到十公里外的東西(這應該算是非常的遠了),那它的精確度還是有約 0.6 公厘左右。這樣的精確度一般來說是相當足夠的了。而且 W buffer 也很容易使用,不需要對程式有什麼重大的修改。
目前 W buffer 最大的問題就是支援度不夠。有些顯示晶片根本就不支援 W buffer,而有些則只支援 16 位元的 W buffer。不過,目前很多顯示晶片都已經開始支援 W buffer,所以將來應該會有更多遊戲使用吧!