KMP算法详解

KMP

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普

拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目

的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。

接下来我们先分析三张图，S代表主串，T代表模式串。

当主串 S[i ]与子串T[ j ]失配时，i不回溯，仅j回溯到一个尽量“偏右”的位置k。因此 KPM算法的核心问题是寻找确定k=next[ j ]的

方法。

                                          （1）                                                                                                  （2）                                                                                              （3）

由 (I) ，(II)，和 (III) 我们得到：

T[0 ... k -1] = T[ j - k ... j -1] ＝ T[0 ... next[ j ] -1]

因此得到 k = next [ j ] 的定义(注意下标范围)

以上定义也说明next [j]与主串S无关。

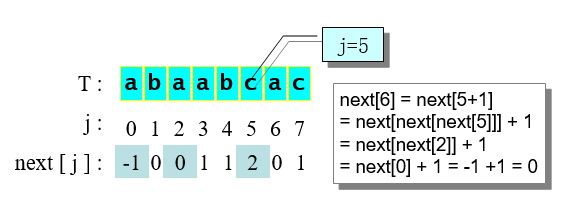
next[ j ]函数举例

kmp算法：

void kmp(int *S,int *T){  
    int i = 0,j = 0;
    getnext(T,next);  
    while(i < n){
        if(j == -1 || S[i] == T[j]){
            i++;
            j++;
        }
        else
            j = next[j];  
        if(j == m){
            printf("%d\n",i-m+1);  
            return ;  
        }  
    }  
    printf("-1\n");  
}  

——根据定义 next[0] = -1;

——设 next[j] = k，求 next[j+1]

            若 T[j] = T[k]，则 next[j+1] = k + 1 = next[j] + 1;

            否则(T[j] !=T[k])，

                若T[[j] = T[next[k]], 则 next[j+1] = next[k] + 1;
                否则......

next[ j ]函数：

void getnext(int *T,int *next){
    int j = 0,k = -1;
    next[0] = -1;    
    while(j < m){
        if(k == -1 || T[j] == T[k]){
            j++; k++;
            next[j] = k;    
        }
        else
            k = next[k];
    }
}

运用KMP算法的匹配过程

第1趟 目标  a c a b a a b aa b c a c aa b c

      模式  a b aa b c a c

    j = 1 ->j=f (j-1)+1 = 0

第2趟 目标  a c a b aa b aa b c a c aa b c

     模式        a ba a b c a c

                              j = 5 ->j =f(j-1)+1= 2

第3趟 目标a c a b aa b aa b c a c aa b c

     模式          (a b)aa b c a c

计算失效函数 f [ j]的方法

首先确定f [0] = -1，再利用f [ j]求f [j+1]。

其中,  f(1)[j] =f[ j],

          f(m)[j ] = f [f(m-1)[j ]]

kmp算法的复杂度是O(n+m)，可以采用均摊分析来解答，具体可参考算法导论。

注意事项：

next数组定义为全局变量时，最好不要命名为next，会与库函数重名，提交时会出现编译错误。。。

练习：

HDU 1711 Number Sequence

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1711

解题思路：http://blog.csdn.net/piaocoder/article/details/41928323

POJ 2406 Power Strings

题目链接：http://poj.org/problem?id=2406

解题思路：http://blog.csdn.net/piaocoder/article/details/47733683

POJ 2752 Seek the Name, Seek the Fame

题目链接：http://poj.org/problem?id=2752

解题思路：http://blog.csdn.net/piaocoder/article/details/47733303

POJ 3461 Oulipo

题目链接：http://poj.org/problem?id=3461

解题思路：http://blog.csdn.net/piaocoder/article/details/47732321