POJ 2488 A Knight's Journey

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 38457		Accepted: 13049

Description

Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

点击打开题目链接

题意：国际象棋中的一匹马，可以从任意位置开始，将棋盘走一遍（每个格子只走一次）

求字典序最小的路径，如果没有合法的路径就输出impossible

分析：dfs，假设棋盘大小为n * m ，我们将棋盘的坐标设置为（1 , 1）-（n , m）

这时从（1,1）开始搜索（纳尼，题中不是说从任意位置开始吗？呵呵，如果不从（1,1）位置开始搜索的话有答案，

那么从（1,1）开始搜索一定也有答案！！！并且此时的答案是字典序最小的，好像很有道理的样子。）

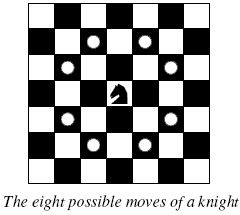
搜索八个方向时我们还要注意搜索的顺序，看看下图：

假设此时小马在 D4 它下一步要搜索的顺序应该为 B3、B5、C2、C6......这样才保证字典序是最小的

代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <iostream>
using namespace std;

const int maxn = 30;
//八个方向的偏移量，注意它的顺序（要求结果为字典序最小的）
const int dir[][2] = {-1,-2, 1,-2, -2,-1, 2,-1, -2,1, 2,1, -1,2, 1,2};
int vis[maxn][maxn];
bool haveAns;
int n, m, t, cas;
void dfs(int x, int y, int cnt, string ans)
{
    if (haveAns) return;        //已经搜到答案，结束搜索
    if (cnt == n * m)           //搜到答案
    {
        cout << ans << endl;
        haveAns = true;
        return;
    }

    for (int i = 0; i < 8; i++) //搜索八个方向
    {
        int tx = x + dir[i][0]; //得到下一个位置的坐标
        int ty = y + dir[i][1];
        if (tx > 0 && tx <= n && ty > 0 && ty <= m && !vis[tx][ty]) //判断坐标的合法性
        {
            vis[x][y] = 1;          //标记为已经搜过
            char c1 = tx + '0';
            char c2 = ty + 'A' - 1;
            dfs(tx, ty, cnt + 1, ans + c2 + c1);    //搜索下一个位置
            vis[x][y] = 0;          //清除标记
        }
    }
}

int main()
{
    cas = 1;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d%d", &n, &m);
        printf("Scenario #%d:\n", cas++);
        haveAns = false;

        memset(vis, 0, sizeof(vis));
        vis[1][1] = 1;
        dfs(1, 1, 1, "A1");         //从坐标(1,1)开始搜索(不用从所有的点开始)

        if (haveAns == false) printf("impossible\n");
        printf("\n");
    }

    return 0;
}