白话空间统计之:Moran's I(莫兰指数)
首先,Moran's I这个东西,官方叫做:莫兰指数,是澳大利亚统计学家帕特里克·阿尔弗雷德·皮尔斯·莫兰(Patrick Alfred PierceMoran)(好长的名字,不过一般都简称为:帕克·莫兰,就是下图这位中年帅哥了),在1950年提出的。这一年,朝鲜战争爆发。
莫兰同学1917年出生在澳大利亚的悉尼,后来考入了剑桥大学,第二次世界大战的时候,加入了盟军,并且因为在数学和物理学上面的特长,被安排在剑桥大学的外弹道学实验室(External Ballistics Laboratory)负责火箭的研究工作。战争结束后,任教于牛津大学,并且就在牛津任教期间,提出了关于莫兰指数的问题。
另外再加一点点小花絮,莫兰同学终生未获得博士学位,但是据他晚年回忆,他似乎对这个事情一直感到骄傲(自己并非博士,但是带出了无数的博士生)。
那么莫兰指数到底是个啥东西呢?莫兰指数一般是用来度量空间相关性的一个重要指标。
一般说来,莫兰指数分为全局莫兰指数(GlobalMoran's I)和安瑟伦局部莫兰指数(AnselinLocal Moran's I)后者是美国亚利桑那州立大学地理与规划学院院长Luc Anselin教授在1995年提出的,后面我们会说到。
今天就简单说说全局莫兰指数,也是狭义上的莫兰指数。
莫兰指数是一个有理数,经过方差归一化之后,它的值会被归一化到-1.0——1.0之间。(如果有喜欢看数学公式的,我最后贴出了全局莫兰指数的计算公式,这里是科普性质的,我就不贴数学公式来虐待大家的大脑了。
当然,这个归一化是一般的情况,根据某些特殊的情况,也会计算出一些不在这个范围内的值,最后来讨论为什么会超出这个范围。
全局莫兰指数计算完成之后,全部的要素,就会给出你一个关于全部数据的相关性的数值(反之,局部莫兰指数,就每个要素都会给你一个相关性数值了,这个以后在说)。所以我们可以根据他给出的值,来看当前你需要计算的数据结果了。
Moran's I >0表示空间正相关性,其值越大,空间相关性越明显,Moran's I <0表示空间负相关性,其值越小,空间差异越大,否则,Moran's I = 0,空间呈随机性。
这里需要注意一下啊,空间差异和空间异质性是不同的概念。
空间差异(spatialdisparity)是指不同地域范畴因为(社会、经济等)发展水平及其结构不同,而产生的差异。
而空间异质性(spatialheterogeneity)是指因为空间位置的不同而引发的获取到不同的数据。
所以二者切不可混为一谈。
最后,我们们来看看,什么叫做正相关,什么叫做负相关。
所谓的相关,就是指相互关系,正相关,就是随着自变量的增长,应变量也随着增长,比如虾神的年纪和血压,就是标准的正相关……。而负相关当然就是相反了,随着自变量的增长而减少,比如虾神的年纪和体力……
那么空间上面的正相关,就是指随着空间分布位置(距离)的聚集,相关性就也就越发显著。空间上的负相关就正好相反了,随着空间分布位置的离散,反而相关性变得显著了。
像如下我采用中国行政区划计算出来的结果:
整个图表可以看出来,人口数和患病的人数,都与空间信息成正相关,就是说,空间分布聚集度大的地方,人口数和患病人数也相应多。
但是可以看见的,患病人数,随着时间推移,他的莫兰指数在上升,而人口数随着年份,莫兰指数在下降,这说明了中国人口的数量慢慢的与空间分布的相关性在减弱,而患病人数与空间分布的相关性在增加。
当然,莫兰指数只是在衡量空间相关性时候的一个重要指标,并不完全能够代表空间相关性,还需要有其他的数据进行验证和综合考量。
下面部分部分仅供不怕死脑细胞的同学参考:(来源于ArcGIS for Destkop的帮助文档)
1、全局莫兰指数的公式:

2、刚才讨论了,莫兰指数一般是在 -1——1之间,那么有时候突然算出来超出这个区间的数据,是怎么回事呢?是不是软件出了bug?
答案是和软件bug无关。
通常,Global Moran's I 指数介于 -1.0 到 1.0 之间。是只有对我们权重进行了行标准化(行标准化的意思,就是在做空间距离矩阵的时候,对矩阵中的每一行,求和后,每个元素除以所在行元素之和这种标准化操作)时才会这样。如果没有对权重进行行标准化处理,则指数值可能会落在-1.0 到 1.0 的范围之外,这表示参数设置有问题。最常见的问题如下:
- 输入的数据严重偏斜(创建数据值的直方图可了解此情况),空间关系的概念化或距离范围的设置使得某些要素的相邻要素非常少。Global Moran's I 统计量是渐进正态的,这意味着,对于偏斜数据,每个要素至少需要具有 8 个相邻要素。为距离范围或距离阈值参数计算的默认值可确保每个要素至少具有 1 个相邻要素,但这可能不够,尤其是在输入数据中的有的值出现严重偏斜时。
- 使用反距离空间关系的概念化,并且反距离非常小。
关于反距离过小的问题,是因为在选择反距离的幂的时候,为了突出拉伸,选择了一个过高的幂,这样就会把反距离(距离的倒数)变得非常的小。看下面关于反距离中幂的说明:
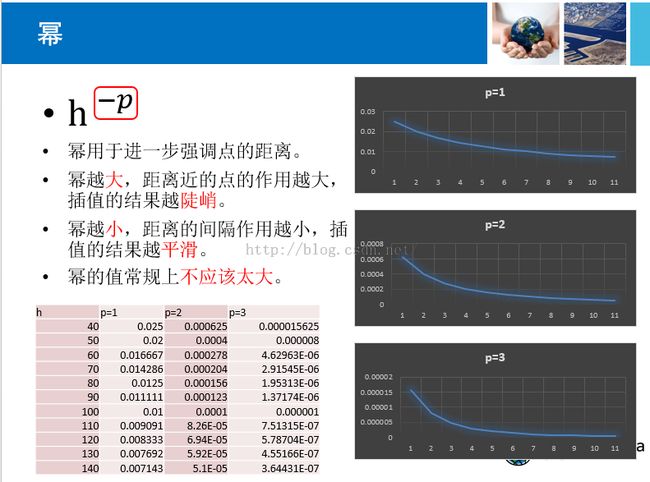
3.未选择行标准化,但应选择。除非聚合方案与所分析的字段直接相关,否则,只要对数据进行了聚合处理,就应选择行标准化。
好,关于全局莫兰值的介绍今天先到这里,下次我们来看看在ArcGIS里面如何使用这个工具来进行计算。
