图像数据到网格数据-3——Cuberille算法

前言

　　这是本博客网格生成算法系列的第三篇，第一篇里面介绍了最为流行的MarchingCubes算法，第二篇中使用新三角形表来对MC算法进行了简化改进，形成了SMC算法。而这篇将介绍一种新的不同与MC算法思路的新网格生成算法，叫做Cuberille法，这种算法的思想相比MC算法要简单，更加易于实现。

 

体素立方体模型

　　根据第一篇的介绍，我们知道MC算法的基本模型是把组成三维图像的体素都当作空间上的点而8体素组成的体元作为立方体单元。相比于MC算法，Cuberille算法是把体素都想象成立方体，而没有所谓体元的概念了。这一点其实更加符合人们对图像的最初认识，最初接触到计算机中的二维图像的时候，一般人理解像素都是将其当成一个涂了颜色的小方块。而Cuberille算法的理解正是把组成三维图像的体素也当成涂了颜色的小立方体块。例如一个三维图像中所有的实点（这里的实点和MC算法里一样指的是内容区域的体素，下文的虚点同理指背景区域的体素）组成一个猪头的形状，那么就可以认为这个猪头是很多很小的立方体方块堆砌而成的。

猪头		三维图像中的猪头体素方块集合

 

基于正方形片为边界建模

　　使用小立方体堆砌组成内容区域，那么这个内容区域的边界必然就是很多正方形面片组成的Mesh，由于每个正方形面片能分成两个三角形面片，那么实际上这个表面的Mesh也是三角网格。下文的重点是研究如何找到这些组成边界面的小正方形面片。

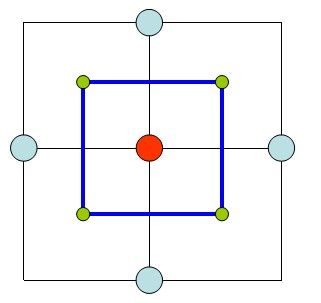
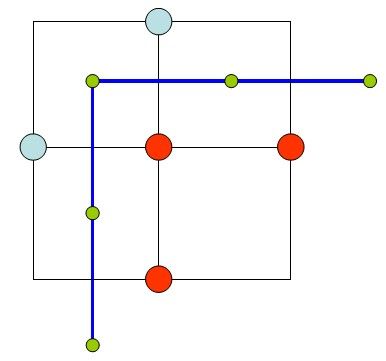
　　首先，小正方形面片总是介于实点和虚点之间，下图使用二维的情况来说明这个边界。

例子1		例子2		说明

　　可以看出，实点和虚点的边界面总是存在一个边界，其长度等于单位长度。那么只要找到图像中所有这样的虚实点交界处的边界，将其焊接起来就能组成内容的表面模型。

　　因而总结出Cbuerille算法的主题思路如下：

1. 创建一个空的Mesh
2. 按层、列、行三重循环遍历所有的体素V
   1. 假如V为实点
      1. 获取V的六邻域体素集合Adj6(V)
      2. 遍历Adj6(V)中的体素T
         1. 若T超出图像范围或者T为虚点
         2. 创建介于V与T之间的正方形片，并加入到Mesh

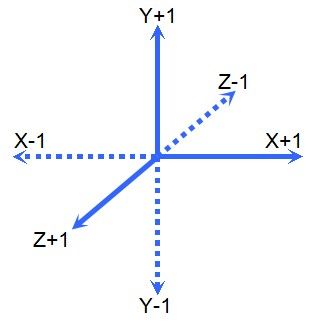
　　下一步就是探讨如何来为实体素V和它的6邻接邻居虚点T（这个T也可能是超出图像范围的点，这里当其为虚点也一样的处理）中间建立方形片并加入到Mesh。为了实现高效统一的创建面片的方案，有必要对邻域和顶点进行编号。下图是一个邻域编号。显示了一个体素六个方向邻域的编号与对应坐标计算方式：

		邻接体素编号 相对偏移 0 （0，1，0） 1 （0，-1，0） 2 （1，0，0） 3 （-1，0，0） 4  （0，0，1） 5 （0，0，-1）
6邻域指示	6邻域邻接体素编号	邻接体素方位对照表

　　同时为了表示立方体8个体素位置的顶点，我们也为他进行编号如下图表所示：

	体素编号 体素偏移 0 （0，1，1） 1 （1，1，1） 2 （1，0，1） 3 （0，0，1） 4 （0，0，0） 5 （1，0，0） 6 （1，1，0） 7 （0，1，0）
预览图	体素方位对照表

　　这样一个立方体的6个正方形面里的三角形组成就可以使用下面的图表来表示：

	邻接方位编号 方位描述 三角形顶点索引 0 上面 （0，1，6） （0，6，7） 1 下面 （3，4，5） （3，5，2） 2 右面 （1，2，5） （1，5，6） 3 左面 （0，7，4） （0，4，3） 4 前面 （0，3，2） （0，2，1） 5 后面 （4，7，6） （4，6，5）
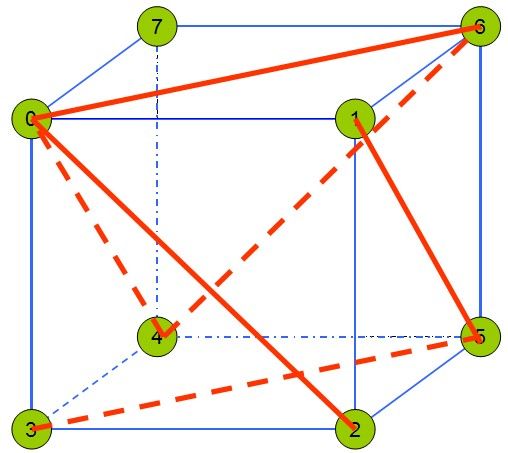预览图（只标示出了前方向的正方形）	三角形顶点对照表

　　这样只需要知道T是V的第几个邻居就可以创建三角片了。下面的步骤描述了这个逻辑过程。

1. 根据T的索引 r 找出其第一个三角片的三个顶点索引。
2. 根据三个顶点索引找出三个顶点坐标偏移量
3. 使用V的坐标加上偏移量计算出三角形三个顶点的坐标位置
4. 创建并添加这个三角形。
5. 根据T的索引 r 找出其第二个三角片的三个顶点索引。
6. 根据三个顶点索引找出三个顶点坐标偏移量
7. 使用V的坐标加上偏移量计算出三角形三个顶点的坐标位置
8. 创建并添加这个三角形。

　　注意这里对偏移量做了一些处理，本来应该的偏移量应该是用浮点数0.5来组成的，如下图所示，焊接点都处在体素位置中点处，所以三角形顶点都应该是“X.5”形式的浮点数。而上文的过程中使用的偏移量（如顶点对应表中的偏移量）是将所有点的坐标都加了0.5之后的位置。之所以使用平移0.5之后的坐标，是希望利用整数点坐标来使用哈希表焊接。那么有必要在算法结束的时候把所有的点坐标-0.5来恢复真正的位置。不过有时由于只需要结果的形状一致，所以也不做处理。

　　最后是用C#实现的Cuberille算法的代码，其中涉及到的bitmap类，哈希表类，Meshbuilder类在前几篇文章中多次提到过，就不重复粘贴代码了。

public struct Int16Triple
{
    public int X;
    public int Y;
    public int Z;
    public Int16Triple(int x, int y, int z)
    {
        X = x;
        Y = y;
        Z = z;
    }
}
public struct FloatTriple
{
    public float X;
    public float Y;
    public float Z;
    public FloatTriple(float x, float y, float z)
    {
        X = x;
        Y = y;
        Z = z;
    }
}
public class CuberilleProcessor
{
        public static Int16Triple[][] AdjIndexToVertexIndices = new Int16Triple[6][]
        {
            new Int16Triple[2] { new Int16Triple(0, 1, 6), new Int16Triple(0, 6, 7) },
            new Int16Triple[2] { new Int16Triple(3, 4, 5), new Int16Triple(3, 5, 2) },
            new Int16Triple[2] { new Int16Triple(1, 2, 5), new Int16Triple(1, 5, 6) },
            new Int16Triple[2] { new Int16Triple(0, 7, 4), new Int16Triple(0, 4, 3) },
            new Int16Triple[2] { new Int16Triple(0, 3, 2), new Int16Triple(0, 2, 1) },
            new Int16Triple[2] { new Int16Triple(4, 7, 6), new Int16Triple(4, 6, 5) },
        };
    public static Int16Triple[] VertexIndexToPositionDelta = new Int16Triple[8]
    {
            new Int16Triple(0, 1, 1),
            new Int16Triple(1, 1, 1),
            new Int16Triple(1, 0, 1),
            new Int16Triple(0, 0, 1),
            new Int16Triple(0, 0, 0),
            new Int16Triple(1, 0, 0),
            new Int16Triple(1, 1, 0),
            new Int16Triple(0, 1, 0),
    };
    BitMap3d bmp;
    public CuberilleProcessor(BitMap3d bitmap)
    {
        bmp = bitmap;
    }
    public Mesh GeneratorSurface()
    {
        int Width = bmp.width;
        int Height = bmp.height;
        int Depth = bmp.depth;
        Int16Triple[] adjPoints6 = new Int16Triple[6];
        MeshBuilder_IntegerVertex mb = new MeshBuilder_IntegerVertex(bmp.width, bmp.height, bmp.depth);
          
        for (int k = 0; k <= Depth - 1; k++)
        {
            for (int j = 0; j <= Height - 1; j++)
            {
                for (int i = 0; i <= Width - 1; i++)
                {
                    if (IsInside(i,j,k))
                    {
                        Int16Triple p = new Int16Triple(i, j, k);
                        InitAdj6(adjPoints6,p);
                        for (int r = 0; r < adjPoints6.Length; r++)
                        {
                            Int16Triple t = adjPoints6[r];
                            if (!IsInside(t.X,t.Y,t.Z))
                            {
                                ExtractSquare(r,p,mb);
                            }
                        }
                    }
                }
            }
        }
        Mesh m= mb.GetMesh();
        for (int i = 0; i < m.Vertices.Count; i++)
        {
            Point3d p = m.Vertices[i];
            p.X -= 0.5f;
            p.Y -= 0.5f;
            p.Z -= 0.5f;
        }//若需要真实位置，则都得平移回去
        return m;
    }

    private void ExtractSquare(int r,Int16Triple p, MeshBuilder_IntegerVertex mb)
    {
        int p0x, p0y, p0z, p1x, p1y, p1z, p2x, p2y, p2z;//
        Int16Triple deltaA0 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][0].X];
        Int16Triple deltaA1 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][0].Y];
        Int16Triple deltaA2 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][0].Z];
        p0x = p.X + deltaA0.X;
        p0y = p.Y + deltaA0.Y;
        p0z = p.Z + deltaA0.Z;
        p1x = p.X + deltaA1.X;
        p1y = p.Y + deltaA1.Y;
        p1z = p.Z + deltaA1.Z;
        p2x = p.X + deltaA2.X;
        p2y = p.Y + deltaA2.Y;
        p2z = p.Z + deltaA2.Z;
        mb.AddTriangle(new Int16Triple(p0x, p0y, p0z), new Int16Triple(p1x, p1y, p1z), new Int16Triple(p2x, p2y, p2z));


        Int16Triple deltaB0 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][1].X];
        Int16Triple deltaB1 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][1].Y];
        Int16Triple deltaB2 = VertexIndexToPositionDelta[AdjIndexToVertexIndices[r][1].Z];

        p0x = p.X + deltaB0.X;
        p0y = p.Y + deltaB0.Y;
        p0z = p.Z + deltaB0.Z;
        p1x = p.X + deltaB1.X;
        p1y = p.Y + deltaB1.Y;
        p1z = p.Z + deltaB1.Z;
        p2x = p.X + deltaB2.X;
        p2y = p.Y + deltaB2.Y;
        p2z = p.Z + deltaB2.Z;
        mb.AddTriangle(new Int16Triple(p0x, p0y, p0z), new Int16Triple(p1x, p1y, p1z), new Int16Triple(p2x, p2y, p2z));
    }
    public virtual bool IsInside(int x, int y, int z)
    {
        if (x <= 0 || y <= 0 || z <= 0 || x > bmp.width || y > bmp.height || z > bmp.depth)
            return false;
        else
        {
            return bmp.GetPixel(x, y, z) == BitMap3d.WHITE;
        }
    }//judge if a voxel is inside the surface

    public static void InitAdj6(Int16Triple[] adjPoints6,Int16Triple p)
    {
        adjPoints6[0].X = p.X;
        adjPoints6[0].Y = p.Y + 1;
        adjPoints6[0].Z = p.Z;

        adjPoints6[1].X = p.X;
        adjPoints6[1].Y = p.Y - 1;
        adjPoints6[1].Z = p.Z;

        adjPoints6[2].X = p.X + 1;
        adjPoints6[2].Y = p.Y;
        adjPoints6[2].Z = p.Z;

        adjPoints6[3].X = p.X - 1;
        adjPoints6[3].Y = p.Y;
        adjPoints6[3].Z = p.Z;

        adjPoints6[4].X = p.X;
        adjPoints6[4].Y = p.Y;
        adjPoints6[4].Z = p.Z + 1;

        adjPoints6[5].X = p.X;
        adjPoints6[5].Y = p.Y;
        adjPoints6[5].Z = p.Z - 1;
    }//initialize poistions of the 6-adjacency points
}

 

算法结果

　　算法使用Engine.raw数据，生成的Cuberille表面放大后的效果图如下，可以看出确实是由方块组成的模型：

　　同时使用SMC算法对Engine数据生成表面，放在一起进行对比呈现，同时比较他们的网格规模的图表如下：

-	SMC算法	Cuberille算法
预览图
顶点数	216147	311263
三角形数	432370	622638

　　可以看出Cuberille的显示效果显然不如SMC算法平滑（自然也不会比经典MC算法平滑），同时相比SMC算法输出规模更大。这些都是Cuberille算法的缺点，所以现在实际应用场合中较少使用这个算法，不过在一些特殊场合，还是会见到这个算法的身影。

　　本文的代码可见本人的github：https://github.com/chnhideyoshi/SeededGrow2d