Maximal Rectangle
地址:https://oj.leetcode.com/problems/maximal-rectangle/
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
首先吐槽下这个题目,不知道是我英语理解还是题目本身存在让人误解地方,我理解题意是最大的矩形包括所有1元素,按着这个理解我很开心的写了如下代码:代码思路很简单,类似杨氏矩阵中用到的思想:http://blog.csdn.net/huruzun/article/details/28420545
public class Solution {
private char[][] matrix ;
public int maximalRectangle(char[][] matrix) {
if(matrix.length == 0){
return 0;
}
int row = matrix.length;
int col = matrix[0].length;
int ans = 0;
this.matrix = matrix;
Point start = new Point();
Point end = new Point(row-1,col-1);
while(true){
if(isAllZeroDown(start, row)){
start.y = start.y+1 >=col ? col-1:start.y+1;
if(start.equals(end)){
return 0;
}
}
if(isAllZeroLeft(start, col)){
start.x = start.x+1 >=row ? row-1:start.x+1;
if(start.equals(end)){
return 0;
}
}
if(!isAllZeroDown(start, row) && !isAllZeroLeft(start, col)){
break;
}
}
while(true){
if(isAllZeroRight(end)){
end.y = end.y-1>= 0 ? end.y-1:0;
}
if(isAllZeroUp(end)){
end.x = end.x-1>= 0 ? end.x-1:0;
}
if(!isAllZeroRight(end) && !isAllZeroUp(end)){
break;
}
}
ans = Math.abs((end.x-start.x+1)*(end.y - start.y+1));
return ans;
}
boolean isAllZeroDown(Point p,int len){
int j = p.y;
for(int i=p.x;i<len;i++){
if(matrix[i][j]=='1'){
return false;
}
}
return true;
}
boolean isAllZeroLeft(Point p,int len){
int i = p.x;
for(int j=p.y;j<len;j++){
if(matrix[i][j]=='1'){
return false;
}
}
return true;
}
boolean isAllZeroUp(Point p){
int i = p.x;
for(int j=p.y;j>=0;j--){
if(matrix[i][j]=='1'){
return false;
}
}
return true;
}
boolean isAllZeroRight(Point p){
int j = p.y;
for(int i=p.x;i>=0;i--){
if(matrix[i][j]=='1'){
return false;
}
}
return true;
}
}
提交之后始终不对,然后开始网上搜索,才发现题目正确意思是:
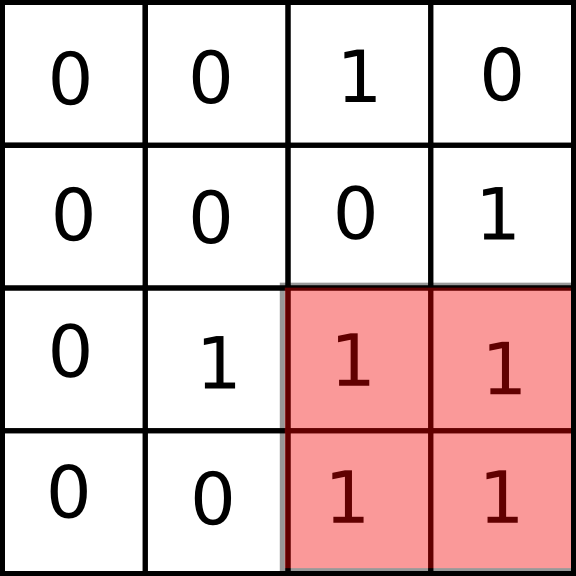
找一个最大矩阵,里面全部是1。
例如下图:
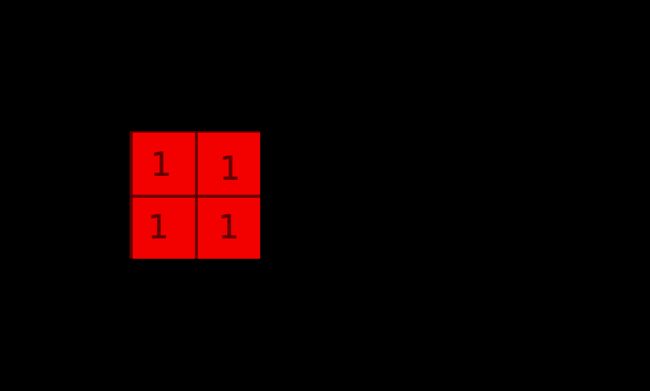
根据这个图转换可以发现问题,看下图:
转到这个图就会发现,这就是:http://blog.csdn.net/huruzun/article/details/39717501里面说到的相同问题。
java代码:
public class Solution {
public int largestRectangleArea(int[] height) {
int maxarea = 0;
Stack<Integer> sta = new Stack<>();
int top ;
int top_area;
int i = 0;
while(i<height.length){
if(sta.isEmpty() || height[sta.peek()]<=height[i] ){
sta.push(i++);
}else{
top = sta.pop();
top_area = height[top] * (sta.isEmpty()? i:i-sta.peek()-1);
if(top_area>maxarea){
maxarea = top_area;
}
}
}
while(!sta.isEmpty()){
top = sta.pop();
top_area = height[top] * (sta.isEmpty()? i:i-sta.peek()-1);
if(top_area>maxarea){
maxarea = top_area;
}
}
return maxarea;
}
public int maximalRectangle(char[][] matrix){
if(matrix.length == 0){
return 0;
}
int row = matrix.length;
int col = matrix[0].length;
int [][]dp = new int[row][];
for(int i=0;i<row;i++){
dp[i] = new int[col];
}
for(int j=0;j<col;j++){
if(matrix[0][j]=='1'){
dp[0][j] = 1;
}
}
for(int j=0;j<col;j++){
for(int i=1;i<row;i++){
if(matrix[i][j] == '1'){
dp[i][j] = dp[i-1][j]+1;
}
}
}
int maxarea = 0;
for(int i=0;i<row;i++){
int temp = largestRectangleArea(dp[i]);
if(temp>maxarea){
maxarea = temp;
}
}
return maxarea;
}
}