Dijkstra算法求解单源点到其余各顶点的最短距离

 单源点最短路径：

        给定带权有向图G和源点v, 求从v到G中其余各顶点的最短路径。

Dijkstra算法：

        Dijkstra提出了一个按路径“长度”递增的次序，逐步得到由给定源点到图的其余各点间的最短路径的算法：
        假设我们以邻接矩阵cost（代码中为A[ ]数组），表示所研究的有向网的代价矩阵。
        迪杰斯特拉算法需要一个顶点集合，初始时集合内只有一个源点V0 ，以后陆续将已求得最短路径的顶点加入到集合中，到全部顶点都进入集合了，过程就结束了。集合 可用一维数组来表示，设此数组为S（代码中为mark[ ]数组），凡在集合S以外的顶点，其相应的数组元素S[i]  为 -1 ，否则为 1 。

        另需一个一维数组D（代码中为dis[ ]数组），每个顶点对应数组的一个单元，记录从源点到其他各顶点当前的最短路径长度，其初值为D[i]=cost[V0][i]，i=1…n。数组D中的数据随着算法的逐步进行要不断地修改
        定义了S集合和D数组并对其初始化后，迪杰斯特拉算法在进行中，都是从S之外的顶点集合中选出一个顶点w，使D[w]的值最小。于是从源点到达w只通过S中的顶点，把 w 加入集合S中，并调整D中记录的从源点到集合中每个顶点v的距离： 取D[v]和D[w]+cost[w][v]中值较小的作为新的D[v]
        重复上述，直到S中包含V中其余各顶点的最短路径。

实例：

                  

代码及解析：

package utils;

import java.io.File;
public class ShortestPath {
	static int INF = Global.INF;

	public static void dijkstraShortestPath(int v,int[][] A){
		
		int n = A[0].length;
		
		int[] dis = new int[n];
		int[] path = new int[n];
		int[] mark = new int[n];
		
		for(int i=0;i<n;i++){
			dis[i] = A[v][i];
			path[i] = v;
			mark[i] = -1;
		}
		
		mark[v] = 1;
		dis[v] = 0;
		
		
		int k = v;
		for(int i =1 ; i<n;i++){  //考察剩余的n-1个节点
			int min = Global.INF;
			for(int j = 0;j<n;j++){//找出本轮对应路径最短的节点
				if((mark[j]!=1)&&(dis[j]<min)){
					min = dis[j];
					k = j;
				}
			}
			mark[k] = 1;//将找出的最短路径对应的节点k加入集合S中
			for(int j =0;j<n;j++){//用上面新加入的节点k来更新dis[]
				if((mark[j]!=1)&&(A[k][j]<Global.INF)&&(min+A[k][j]<dis[j])){//不加A[k][j]<Global.INF的话，如果A[k][j]=Global.INF
					                             //min+A[k][j]就会得到一个很大的负数使得<dis[j]成立使程序出错
					dis[j] = min+A[k][j];
					path[j] = k ;
				}
			}
		}
		
		//打印
		for(int i =0;i<n;i++){
			if(i!=v){
				System.out.print("v"+v+"到v"+i+"的最短距离为：");
				if(mark[i]!=1){//if(!(dis[i]<Global.INF)){//
					//System.out.print("无");
					System.out.print("无");
				}else{
				System.out.println(dis[i]);
				}
				
				//逆序打印路径方式，这次打印主要是为了看清楚path[]的作用，path[i]存储的是对应最短路径上的i的前驱结点
				if (mark[i] != -1) {// 存在最短路径
					System.out.print("v" + v + "到v" + i + "的最短路径为：");
					int prePath = i;
					while (prePath != v) {
						System.out.print(prePath + "<-");
						prePath = path[prePath];
					}
					System.out.println(v);
				}
				
				//正序打印路径的方式
				String pathStr = ""+i;
				String tmpStr = "";
				
				if (mark[i] != -1) {// 存在最短路径
					System.out.print("v" + v + "到v" + i + "的最短路径为：");
					int prePath = i;
					while (prePath != v) {
						//System.out.print(prePath + "<-");
						
						prePath = path[prePath];
						tmpStr = prePath + "->";
						pathStr = tmpStr + pathStr;
					}
					System.out.print(pathStr);
				}
				System.out.println("\n");
			}
			
		}
	}
	
	public static void computeShortestPathOfEachPairNodes(){
		int[][] A = {//测试
				{0,4,11},
				{6,0,2},
				{3,Global.INF,0}
		};
		int n = A[0].length;
		
		for(int i =0;i<n;i++){
			dijkstraShortestPath(i,A);
		}
	}
	public static void main(String[] args) {
		//floydShortestPath();
		
		int[][] A = {//测试
		{INF,INF, 10, INF, 30,100 },
		{INF,INF, 5,  INF, INF,INF},
		{INF,INF, INF,50,  INF,INF},
		{INF,INF, INF,INF, INF,10 },
		{INF,INF, INF,20,  INF,60 },
		{INF,INF, INF,INF, INF,INF},
		};
		int v0 = 0;//求解v0到各节点的最短路径
		dijkstraShortestPath(v0,A);
		
		//computeShortestPathOfEachPairNodes();//与Floyd做对比
	}
}

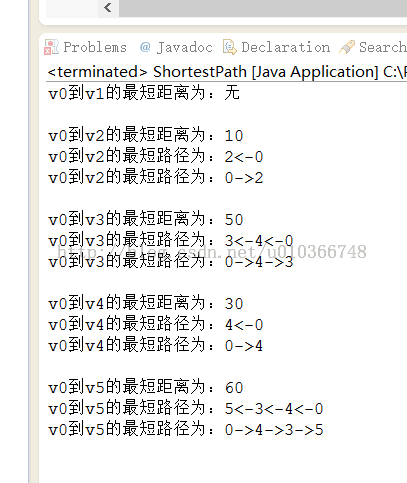
测试结果：