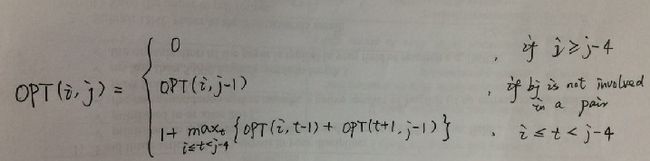算法课笔记系列(三)—— 动态规划
这两周都太忙,所以上周也没总结。这周一起补上。
上周讲的是Matroid,一个非常抽象的概念,中文翻译为“拟阵”。这个内容放到下一篇博文中。这篇总结一下这周讲的“动态规划(Dynamic Programming, 简称DP)”。动态规划可以应用在生物信息学,控制理论,信息理论,运筹学(Operations research)和计算机科学中的理论、图像、人工智能、编译器等等。
首先,对着之前的算法思路进行一个对比:
【贪心算法】是对问题增量地建立一个解决方法,仅考虑当前情况下的最优,并不断优化标准;
【分治算法】是将一个问题分解为若干个规模相等的子问题,解出子问题,然后将子问题的解进行组合,得到原问题的解;
而【动态规划】,则是将一个问题分解为有重合部分的子问题,将子问题的解不断地扩大成更大的子问题的解,最终得出满足条件的原问题的解。
针对课堂上讲的案例,这里做了一个list总结:
(1)Weighted Intervan Scheduling
是不是觉得跟之前的贪心算法中的区间调度的例子很像?哈哈~其实就是一个问题,不过与之前贪心算法中不同的是,该区间调度是对每一个时间段给了一个权重,要解决的问题是同时兼容的任务的含有最大权重的子集。
当然,当所有任务的权重都等于1的时候,就变成典型的贪心算法了。我们回忆一下,在贪心算法中,对于该问题,我们是考虑最早结束时间,如果一个任务与之前选中的任务可以兼容,那么就加入到集合中。但是这种思路在权重任意并且不定的情况下是不可行的。反例如下:
对于该问题的考虑如下,首先按照任务的结束时间先后对任务进行排序编号,为f1,f2,…fn, 定义p(j)是任务i与任务j兼容的最大的索引项i。令OPT(j)为问题的最优解,包含任务1,2…任务j。
第一种情况:OPT选择任务j
此时,需要将任务j的权重加进来,不能加入不兼容的任务{p(j)+1,…,j-1},包含剩下的兼容的任务1,2,…p(j)问题的最优解。
第二种情况:OPT不选择任务j
这样,OPT一定包含剩下的兼容的任务1,2,…j-1问题的最优解。
针对该算法,使用暴力算法的话将会使得复杂度指数级增长,因此采用制表法/记忆法(Memoization), 将每一个子问题的结果放在一个缓存中;可以是一个查找表。
(2)Segmented Least Squares
给出一个平面中的n个点:(x1,y1), (x2, y2),…(xn,yn).目标是找到一条直线y = ax + b使得所有点与该直线上的垂直点的平方差的和最小。
(3)背包问题
有一个背包和n个物品,第i个物品的重量为wi(kg)>0,价值为vi>0。背包的容量为W(kg),目标是装满背包使得总价值最大。
这是最典型的动态规划的算法之一。
(4)RNA secondary Structure
有一个字符串B =b1b2,…bn. 全为字母{A, C, G, U}组成。因为RNA是单链的结构,因此可以扩展为回环,组成碱基对。这样的结构对于理解分子结构很重要,该结构称为RNA的二级结构。目标是给定一个分子B = b1b2,…bn,找出一个二级结构S能够最大化碱基对的数目
(5)序列对齐
给定两个字符串,找出两个字符串对齐的最小损耗(可gap)。如下图所示:
后面几个问题的分析暂时没写,先把结论放这里。最近实在是太忙,有时间会补上。