拉格朗日乘数
说起拉格朗日乘子法,印象中其实高中都用过,用来求条件极值。大学中,高等数学里面也曾经提到过,印象依然没有什么改变,就是用来求条件极值。研究僧,老板让看SVM,知道SVM是通过拉格朗日方法把原始问题转化对w、b和a的极大极小问题,之后又在许多论文中看到这货的身影。然而从来没有仔细想过,为什么拉格朗日乘子法可以这么吊。
直到有次听课,讲到《致命魔术》里面的一句话,Are u watching closely? You just wanna be fooled。
突然发现,对于看书及看论文过程中接触到的一些方法和公式,I just wanna be fooled。因为这样简单、不费事。然而从来没有想过去watching closely,然而这样做的后果就是...完全不能充分理解各种算法就概念,于是我觉得逼自己去watching closely and don't be fooled
于是,我觉得先从拉格朗日这货开始,见解可能是错的,但是就算是错误的道路,最起码我也已经在路上。
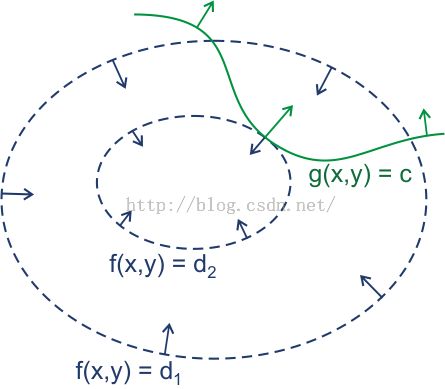
wiki上是这样的,假设有函数:,要求其极值(最大值/最小值),且满足条件g(x,y)=c,
c为常数。对不同的值,不难想像出
点击打开链接当时看的时候也是迷迷糊糊的,其实后来再看,这段解释已经非常的清楚了。不懂的话可以去看下这个视频点击打开链接,个人感觉讲的还是非常不错的,虽然看完还是有些不懂。主要问题还是为什么f和g的梯度平行时为极值。不过下面有一段评论我觉得写得还是蛮好的
“理解拉格朗日乘数法的关键 原来是梯度!
在作为约束条件的等值面g(x,y,z)=constant(二维的话是等值线,更高维就是类似的更高维结构)上函数 w=f(x,y,z) 的梯度的分布是不同的,当w=f(x,y,z)的梯度与g(x,y,z)=constant 等值面不垂直时,自然在所偏的方向还有更大或更小的值,只有垂直时才取到极值,而等值面上的梯度是垂直于等值面的,所以当二者的梯度线性相关时就是取极值处了。”
看完后我的总结是,这里的极值,并没有明确说是极大值或者极小值(视频里也多次强调),而当f的梯度与等值面垂直的那个瞬间,f沿曲面方向是不变的(对应上图就是曲线方向),而在其他点总是要变的更大或者变的更小,因此当f与g的梯度平行时为极值。当然,对这一概念的理解与对梯度的理解是息息相关的。唉..果然又吃了读书少的亏啊。至于,拉格朗日乘数,其实就是两梯度的线性关系![]() 。
。
未完待续...