01背包

分类：             算法分析             动态规划              2012-11-26 15:50     636人阅读     评论(0)     收藏     举报    

http://www.cnblogs.com/hustcat/archive/2010/05/21/1741228.html

动态规划算法是一种经典的算法，它是如此美妙的算法，值得每一个程序员拥有。但是，直到晚上看《算法导论》，才发现自己现在才全面理解它，不禁狂汗。。。

以经典的背包问题来展示动态规划算法

 

 

代码

Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/-->  1 #include <stdio.h>

 #define N    4
 #define W    5

 //物品的重量
 int w[] = {-1, 2, 1, 3, 2};

 //价值数组
 int vi[] = {-1, 12, 10, 20, 15};

 int v[N+1][W+1]; //v[i][j]表示从前i个物品选能够放进承重量为j的背包的子集的最大总价值

 void init()
 {
     int  i, j;
     for (i = 0; i <= N; i++)
         for (j = 0; j <= W; j++)
             v[i][j] = -1;

     for (i = 0; i <= N; i++)
         v[i][0] = 0;

     for (i=0; i <= W; i++)
         v[0][i] = 0;
 }


 //基于备忘录的动态规划算法
 int MKFnapsack_MEMOIZE(int i, int j)
 {
     int value;
     if (v[i][j] < 0)  //如果v[i][j]还没有计算,则进行计算
     {
         if (j < w[i])
             value = MKFnapsack_MEMOIZE(i-1,j);
         else
         {
             int v1 = MKFnapsack_MEMOIZE(i-1, j);
             int v2 = MKFnapsack_MEMOIZE(i-1, j-w[i]) + vi[i];
             value = v1 >=v2 ? v1:v2;
         }
         v[i][j] = value;
     }
     return v[i][j]; //如果v[i][j]已经进行计算,则不进行计算,直接返回即可
 }

 //自顶向下的动态规划算法
 int MKFnapsack_TOP_TO_BOTTOM(int i, int j)
 {
     int value;

     if(i <= 0 || j <= 0)
         return 0;

     //不管v[i][j]是否计算过,都进行计算
     if (j < w[i])
         value = MKFnapsack_TOP_TO_BOTTOM(i-1, j);
     else
     {
         int v1 = MKFnapsack_TOP_TO_BOTTOM(i-1, j);
         int v2 = MKFnapsack_TOP_TO_BOTTOM(i-1, j-w[i]) + vi[i];
         value = v1 >= v2 ? v1:v2;
     }

     return value;
 }

 //自底向上的算法
 int MKFnapsack_BOTTOM_TO_TOP(int Ni, int Wi)
 {
     int i, j;
     for (i = 1; i <= Ni; i++)
     {
         for(j = 1; j <= Wi; j++)
         {
             if(j < w[i])
                 v[i][j] = v[i-1][j];
             else //j >=w[i]
             {
                 int v1= v[i-1][j];
                 int v2 = v[i-1][j-w[i]] + vi[i];
                 v[i][j] = v1 >= v2 ? v1:v2;
             }
         }
     }
     return v[N][W];
 }

 void print_v(int Ni, int Wi)
 {
     int i, j;
     for(i = 0; i <= Ni; i++)
     {
         for(j = 0; j <= Wi; j++)
             printf("%d ", v[i][j]);
         printf("\n");
     }
 }

 int main()
 {
     printf("top to bottom most value is:%d\n", MKFnapsack_TOP_TO_BOTTOM(N, W));

     init();//数组初始化
     printf("memoize most value is:%d\n", MKFnapsack_MEMOIZE(N, W));
     print_v(N, W);

     init();
     printf("bottom to top most value is:%d\n", MKFnapsack_BOTTOM_TO_TOP(N, W));
     print_v(N, W);

     return 0;
 }

代码 

Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/-->  1 #include <stdio.h>
 
 #define N    4
 #define W    5
 
 //物品的重量
 int w[] = {-1, 2, 1, 3, 2};
 
 //价值数组
 int vi[] = {-1, 12, 10, 20, 15};
 
 int v[N+1][W+1]; //v[i][j]表示从前i个物品选能够放进承重量为j的背包的子集的最大总价值
 
 void init()
 {
     int  i, j;
     for (i = 0; i <= N; i++)
         for (j = 0; j <= W; j++)
             v[i][j] = -1;
 
     for (i = 0; i <= N; i++)
         v[i][0] = 0;
 
     for (i=0; i <= W; i++)
         v[0][i] = 0;
 }
 
 
 //基于备忘录的动态规划算法
 int MKFnapsack_MEMOIZE(int i, int j)
 {
     int value;
     if (v[i][j] < 0)  //如果v[i][j]还没有计算,则进行计算
     {
         if (j < w[i])
             value = MKFnapsack_MEMOIZE(i-1,j);
         else
         {
             int v1 = MKFnapsack_MEMOIZE(i-1, j);
             int v2 = MKFnapsack_MEMOIZE(i-1, j-w[i]) + vi[i];
             value = v1 >=v2 ? v1:v2;
         }
         v[i][j] = value;
     }
     return v[i][j]; //如果v[i][j]已经进行计算,则不进行计算,直接返回即可
 }
 
 //自顶向下的动态规划算法
 int MKFnapsack_TOP_TO_BOTTOM(int i, int j)
 {
     int value;
     
     if(i <= 0 || j <= 0)
         return 0;
 
     //不管v[i][j]是否计算过,都进行计算
     if (j < w[i])
         value = MKFnapsack_TOP_TO_BOTTOM(i-1, j);
     else
     {
         int v1 = MKFnapsack_TOP_TO_BOTTOM(i-1, j);
         int v2 = MKFnapsack_TOP_TO_BOTTOM(i-1, j-w[i]) + vi[i];
         value = v1 >= v2 ? v1:v2;
     }
 
     return value;
 }
 
 //自底向上的算法
 int MKFnapsack_BOTTOM_TO_TOP(int Ni, int Wi)
 {
     int i, j;
     for (i = 1; i <= Ni; i++)
     {
         for(j = 1; j <= Wi; j++)
         {
             if(j < w[i])
                 v[i][j] = v[i-1][j];
             else //j >=w[i]
             {
                 int v1= v[i-1][j];
                 int v2 = v[i-1][j-w[i]] + vi[i];
                 v[i][j] = v1 >= v2 ? v1:v2;
             }
         }
     }
     return v[N][W];
 }
 
 void print_v(int Ni, int Wi)
 {
     int i, j;
     for(i = 0; i <= Ni; i++)
     {
         for(j = 0; j <= Wi; j++)
             printf("%d ", v[i][j]);
         printf("\n");
     }
 }
 
 int main()
 {
     printf("top to bottom most value is:%d\n", MKFnapsack_TOP_TO_BOTTOM(N, W));
 
     init();//数组初始化
     printf("memoize most value is:%d\n", MKFnapsack_MEMOIZE(N, W));
     print_v(N, W);
 
     init();
     printf("bottom to top most value is:%d\n", MKFnapsack_BOTTOM_TO_TOP(N, W));
     print_v(N, W);
 
     return 0;
 }

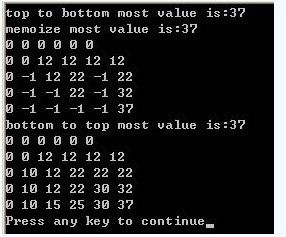
输出结果：

自顶向下的递归算法，写法最简单，但效率是最低的，它往往把问题搞成指数级。而自底向上的算法是DP的经典策略，它比自顶向下的效率高，但是，它往往也计算了没有必要计算的子问题(见上图)。而基于备忘录的自顶向下的算法是前两者的集大成者，效率最优。