B树(B-树)、B+树、AVL树、B*树
看数据结构的时候经常容易被各种树绕晕,所以重新整理下这些 纠结树。
1,B树(B-树)
注意,好多地方都喜欢说B-树,给人一种错觉B-树与B树是两种数据结构,其实是一种。
外文翻译的时候B-tree,有的人喜欢翻译成B-树,有的翻译为B树,所以才造成了这样的错觉。
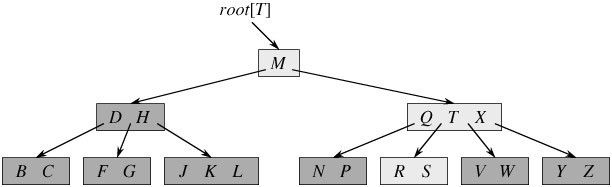
先看看B树的数据结构:
这是从july算法的博客中拿过来的一个图
定义为:一颗m阶的B树是一颗平衡的m路搜索树,它或者为空树,或者满足下列条件:
1,每个结点最多有m个孩子
2,除根结点外,每个非叶子结点至少有[ceil(m/2)]个孩子结点,ceil(表示向上取整)
3,若根节点不是叶子结点,则它至少有2个孩子。
4,有k个孩子的非叶子结点恰好有k-1个关键码,关键码按递增次序排列。
5,所有的叶子结点都在同一层。B树的叶子结点可以看作一种外部结点,不包含任何信息
维基百科的定义:
B树的高度:
若B树某一非叶子节点包含N个关键字,则此非叶子节点含有N+1个孩子结点,而所有的叶子结点都在第K层,我们可以得出
1,因为根节点至少有2个孩子,所以第2层至少有2个结点
2,除根和叶子结点外,其他结点至少有[ceil(m/2)]个孩子,ceil()向上取整
3,第三层至少有2*[ceil(m/2)]个孩子
4,第四层至少有2*[ceil(m/2)^2]个孩子
5 ,第K层至少有2*[ceil(m/2)^(k-2)]个孩子,则N+1>=2*[ceil(m/2)^(k-2)]
6,考虑第K层的结点个数为N+1,那么2*[ceil(m/2)^(k-2)]<=N+1,也就是k层的最少结点数刚好达到N+1个,即: K≤ log┌m/2┐((N+1)/2 )+2;
一棵m阶的B+树和m阶的B树的异同点在于:
1.有n棵子树的结点中含有n-1 个关键字; (此处颇有争议,B+树到底是与B 树n棵子树有n-1个关键字 保持一致,还是不一致:B树n棵子树的结点中含有n个关键字,待后续查证。暂先提供两个参考链接:①wikipedia http://en.wikipedia.org/wiki/B%2B_tree#Overview;②http://hedengcheng.com/?p=525。而下面B+树的图尚未最终确定是否有问题,请读者注意)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)
B+树是B-树的变体,也是一种多路搜索树:
其定义基本与B-树同,除了:
1).非叶子结点的子树指针与关键字个数相同;
2).非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
3).为所有叶子结点增加一个链指针;
4).所有关键字都在叶子结点出现
为了全面 这里给出网上另外一种说法:
一棵m阶的B+树和m阶的B树的差异在于:
1.有n棵子树的结点中含有n个关键字; (而B 树是n棵子树有n-1个关键字)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)
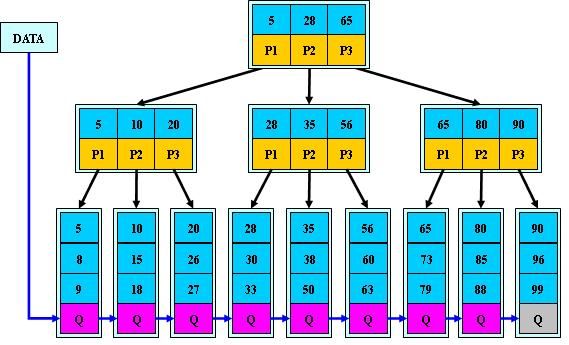
下图给出典型的3阶B+树示例
B+的特性:
1).所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2).不可能在非叶子结点命中;
3).非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4).更适合文件索引系统;
3,B*树
B*Tree是B+树的变体,在B+Tree的非根和非叶子结点(内结点)再增加指向兄弟的指针
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高。
4,AVL树
1. 概述
AVL树是最早提出的自平衡二叉树,在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis。AVL树种查找、插入和删除在平均和最坏情况下都是O(log n),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。本文介绍了AVL树的设计思想和基本操作。
2. 基本术语
有四种种情况可能导致二叉查找树不平衡,分别为:
(1)LL:插入一个新节点到根节点的左子树(Left)的左子树(Left),导致根节点的平衡因子由1变为2
(2)RR:插入一个新节点到根节点的右子树(Right)的右子树(Right),导致根节点的平衡因子由-1变为-2
(3)LR:插入一个新节点到根节点的左子树(Left)的右子树(Right),导致根节点的平衡因子由1变为2
(4)RL:插入一个新节点到根节点的右子树(Right)的左子树(Left),导致根节点的平衡因子由-1变为-2
针对四种种情况可能导致的不平衡,可以通过旋转使之变平衡。有两种基本的旋转:
(1)左旋转:将根节点旋转到(根节点的)右孩子的左孩子位置
(2)右旋转:将根节点旋转到(根节点的)左孩子的右孩子位置
3. AVL树的旋转操作
AVL树的基本操作是旋转,有四种旋转方式,分别为:左旋转,右旋转,左右旋转(先左后右),右左旋转(先右后左),实际上,这四种旋转操作两两对称,因而也可以说成两类旋转操作。
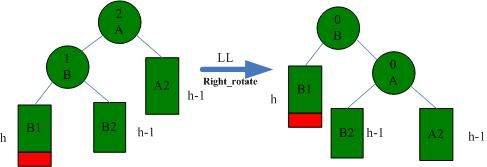
3.1 LL
LL情况需要右旋解决,如下图所示:
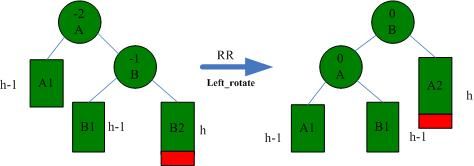
3.2 RR
RR情况需要左旋解决,如下图所示:
代码为:
3.3 LR
LR情况需要左右(先B左旋转,后A右旋转)旋解决,如下图所示:
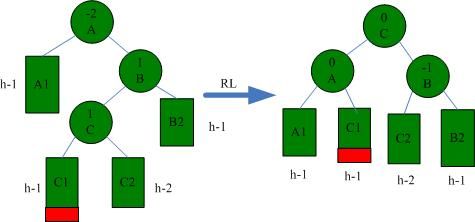
3.4 RL
RL情况需要右左旋解决(先B右旋转,后A左旋转),如下图所示: