GCC's bacl-end & assemble emission (27 - continue)

 

build_automaton (continued)

 

6418   if (progress_flag )

6419     fprintf (stderr , " done/n");

6420   ticker_off (&NDFA_time );

6421   count_states_and_arcs (automaton, &states_num, &arcs_num);

6422   automaton->NDFA_states_num = states_num;

6423   automaton->NDFA_arcs_num = arcs_num;

6424   ticker_on (&NDFA_to_DFA_time );

6425   if (progress_flag )

6426   {

6427     if (automaton->corresponding_automaton_decl == NULL)

6428       fprintf (stderr , "Make anonymous DFA");

6429     else

6430       fprintf (stderr , "Make DFA `%s'",

6431             automaton->corresponding_automaton_decl->name);

6432       fprintf (stderr , " (1 dot is 100 new states):");

6433   }

 

count_states_and_arcs counts the number of states and the transitions of automaton.

 

6387 static void

6388 count_states_and_arcs (automaton_t automaton, int *states_num,            in genautomata.c

6389                      int *arcs_num)

6390 {

6391   curr_counted_states_num = 0;

6392   curr_counted_arcs_num = 0;

6393   pass_states (automaton, incr_states_and_arcs_nums );

6394   *states_num = curr_counted_states_num ;

6395   *arcs_num = curr_counted_arcs_num ;

6396 }

 

5978 static void

5979 pass_states (automaton_t automaton, void (*applied_func) (state_t state)) in genautomata.c

5980 {

5981   curr_state_graph_pass_num ++;

5982   pass_state_graph (automaton->start_state, applied_func );

5983 }

 

Above, curr_state_graph_pass_num at line 6394 ensures every state will be only counted once. We can see this at line 5966 below.

 

5961 static void

5962 pass_state_graph (state_t start_state, void (*applied_func) (state_t state))  in genautomata.c

5963 {

5964   arc_t arc;

5965

5966   if (start_state->pass_num == curr_state_graph_pass_num )

5967     return ;

5968   start_state->pass_num = curr_state_graph_pass_num ;

5969   (*applied_func ) (start_state);

5970   for (arc = first_out_arc (start_state);

5971        arc != NULL;

5972        arc = next_out_arc (arc))

5973     pass_state_graph (arc->to_state, applied_func);

5974 }

 

For every state, incr_states_and_arcs_nums is invoked.

 

6376 static void

6377 incr_states_and_arcs_nums (state_t state)                                              in genautomata.c

6378 {

6379   arc_t arc;

6380

6381   curr_counted_states_num ++;

6382   for (arc = first_out_arc (state); arc != NULL; arc = next_out_arc (arc))

6383     curr_counted_arcs_num ++;

6384 }

 

It is time to transform NDFA to DFA. Continue with build_automaton .

 

build_automaton (continued)

 

6434   NDFA_to_DFA (automaton);

6435   if (progress_flag )

6436     fprintf (stderr , " done/n");

6437   ticker_off (&NDFA_to_DFA_time );

6438   count_states_and_arcs (automaton, &states_num, &arcs_num);

6439   automaton->DFA_states_num = states_num;

6440   automaton->DFA_arcs_num = arcs_num;

6441   if (!no_minimization_flag )

6442   {

6443     ticker_on (&minimize_time );

6444      if (progress_flag )

6445     {

6446       if (automaton->corresponding_automaton_decl == NULL)

6447         fprintf (stderr, "Minimize anonymous DFA...");

6448       else

6449         fprintf (stderr , "Minimize DFA `%s'...",

6450               automaton->corresponding_automaton_decl->name);

6451     }

6452     minimize_DFA (automaton);

6453     if (progress_flag )

6454       fprintf (stderr , "done/n");

6455     ticker_off (&minimize_time );

6456     count_states_and_arcs (automaton, &states_num, &arcs_num);

6457     automaton->minimal_DFA_states_num = states_num;

6458     automaton->minimal_DFA_arcs_num = arcs_num;

6459   }

6460 }

 

The algorithm here transfers NDFA to DFA is very simple. As for our example, from start_state , it can transit to SA, SB or SC. To solve this nondeterministic, we create a new A’, A’ = {SA ∪ SB ∪ SC} – that means it is a composed state triggered by instruction of class (A|B|C) from S, and has all outgoing state transitions from SA, SB and SC. See that the state transiton from S to A’ now is deterministic. Repeating above steps for all states that have nondeterministic transition until no such state exists.

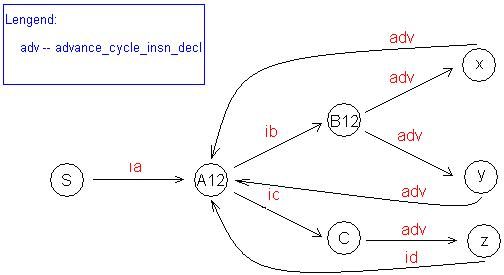
For see the algorithm clearly, consider following automaton.

figure 74  : example of NDFA to DFA, step 1

From every state except state S can find at least one closed loop – it is a must condition for workable chip for any open end means the chip will dead at that point. And notice that start state (S) may not have incoming transition. The example automaton is a NDFA one; see that transition from state S and state A1 are nondeterministic.

figure 75  : example of NDFA to DFA, step 2

Apply the algorithm upon the state A1 and A2, we can get above graph. State A12 is still nondeterministic as instruction class ib can trigger two transitions. See that state A12 is the compound one created from state A1 and A2; we can’t decide its units’ reservation now. Anyway, we don’t need unit reservation any more; all we need now are states and their transitions.

figure 76  : example of NDFA to DFA, step 3

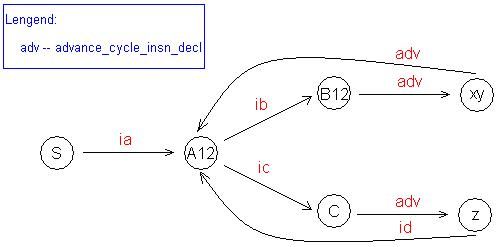
Again combining state B1 and B2, we get above figure, however this state is still nondeterministic as advance_cycle_insn_decl will trigger two state transitions. See that this state B12 even can’t exist during automaton generation.

figure 77  : example of NDFA to DFA, step 4

The deterministic automaton at last reformed is shown in above figure. Notice that the deterministic version and nondeterministic version are equal only in the sense of instruction issue opportunity.

 

5917 static void

5918 NDFA_to_DFA (automaton_t automaton)

5919 {

5920   state_t start_state;

5921   state_t state;

5922   decl_t decl;

5923   vla_ptr_t state_stack;

5924   int i;

5925   int states_n;

5926

5927   VLA_PTR_CREATE (state_stack, 150, "state stack");

5928   /* Create the start state (empty state).  */

5929   start_state = automaton->start_state;

5930   start_state->it_was_placed_in_stack_for_DFA_forming = 1;

5931   VLA_PTR_ADD (state_stack, start_state);

5932   states_n = 1;

5933   while (VLA_PTR_LENGTH (state_stack) != 0)

5934   {

5935     state = VLA_PTR (state_stack, VLA_PTR_LENGTH (state_stack) - 1);

5936     VLA_PTR_SHORTEN (state_stack, 1);

5937     form_arcs_marked_by_insn (state);

5938     for (i = 0; i < description ->decls_num; i++)

5939     {

5940       decl = description ->decls [i];

5941        if (decl->mode == dm_insn_reserv

5942           && create_composed_state

5943              (state, DECL_INSN_RESERV (decl)->arcs_marked_by_insn,

5944               &state_stack))

5945       {

5946         states_n++;

5947         if (progress_flag && states_n % 100 == 0)

5948           fprintf (stderr , ".");

5949       }

5950     }

5951   }

5952   VLA_PTR_DELETE (state_stack);

5953 }

 

Remember that for nondeterministic automaton, in our above example, every alternatives of define_insn_reservation will be evaluated, while for deterministic automaton, only the first qualified alternative will be evaluated. This will make great difference from then on. In fact, when alternatives are handled in detersminstic way, the automaton created is already the deterministic ones.

 

5787 static void

5788 form_arcs_marked_by_insn (state_t state)                                             in genautomata.c

5789 {

5790   decl_t decl;

5791   arc_t arc;

5792   int i;

5793

5794   for (i = 0; i < description ->decls_num; i++)

5795   {

5796     decl = description ->decls [i];

5797     if (decl->mode == dm_insn_reserv)

5798       DECL_INSN_RESERV (decl)->arcs_marked_by_insn = NULL;

5799   }

5800   for (arc = first_out_arc (state); arc != NULL; arc = next_out_arc (arc))

5801   {

5802     if (arc->insn == NULL)

5803       abort ();

5804     arc->next_arc_marked_by_insn

5805          = arc->insn->insn_reserv_decl->arcs_marked_by_insn;

5806     arc->insn->insn_reserv_decl->arcs_marked_by_insn = arc;

5807   }

5808 }

 

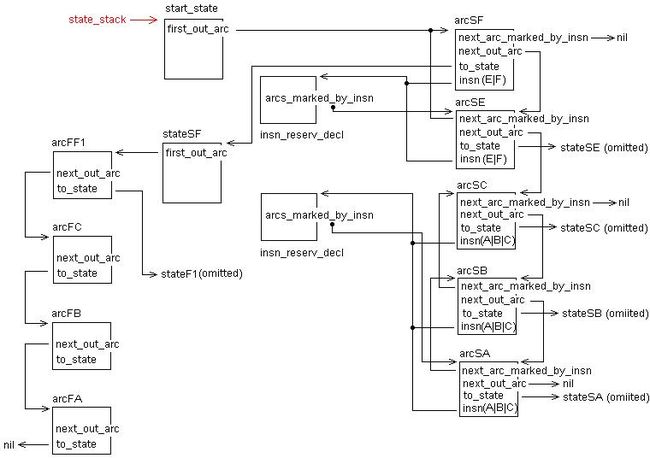
In state can issue instruction containing alternatives, to discriminate these special transitions from other deterministic transitions, form_arcs_marked_by_insn will link these transitions (in form of data of arc) tegother by next_arc_marked_by_insn field.

In nondeterministic example, for start_state , following will be gotten.

For insn (E|F)

arcSF->next_arc_marked_by_insn = NULL (arcSF->to_state = stateSF)

arcSF->insn->insn_reserv_decl->arcs_marked_by_insn = arcSF

arcSE->next_arc_marked_by_insn = arcSF (arcSE->to_state = stateSE)

arcSE->insn->insn_reserv_decl->arcs_marked_by_insn = arcSE (the last value)

For insn (A|B|C)

arcSC->next_arc_marked_by_insn = NULL (arcSC->to_state = stateSC)

arcSC->insn->insn_reserv_decl->arcs_marked_by_insn = arcSC

arcSB->next_arc_marked_by_insn = arcSC (arcSB->to_state = stateSB)

arcSB->insn->insn_reserv_decl->arcs_marked_by_insn = arcSB

arcSA->next_arc_marked_by_insn = arcSB (arcSA->to_state = stateSA)

arcSA->insn->insn_reserv_decl->arcs_marked_by_insn = arcSA (the last value)

(Note that above two parts are linked by next_out_arc field of arc of state S tegother.)

In deterministic example, for start_state, following will be gotten:

For insn A

arcSA->next_arc_marked_by_insn = NULL (arcSA->to_state = stateSA)

arcSA->insn->insn_reserv_decl->arcs_marked_by_insn = arcSA

For insn E

arcSE->next_arc_marked_by_insn = NULL (arcSE->to_state = stateSE)

arcSE->insn->insn_reserv_decl->arcs_marked_by_insn = arcSE

(Note that above two parts are linked by next_out_arc field of arc of state S tegother.)

Showed in figure at below, insn (x1|x2|x3) stands for instruction class that has three alternatives: x1, x2, and x3 in define_insn_reservation. In the figure two arcs_marked_by_insn s are corresponding field of different insn_reserv_decl – the decl for define_insn_reservations pattern.

figure 78  : building DFA, stage 2

Now in state_stack is only state_start . create_composed_state is simple for deterministic automaton, as next_arc_marked_by_insn is always NULL (see the check at line 5853). It will put to_state fetched at line 5832 into state_stack and return. Now in state_stack , there are SA, and SE.

In the nondeterministic automaton example, field component_states is used for the so-called component state (i.e., states A12, B12 and xy in above figures). As to instruction class having alternatives A, B and C, the 1st parameter original_state is start_state , and the 2nd parameter arcs_marked_by_insn refer to the arcs_marked_by_insn s in above figure which is the field of insn_reserv_decl – the decl of define_insn_reservation pattern.

 

5814 static int

5815 create_composed_state (state_t original_state, arc_t arcs_marked_by_insn,      in genautomata.c

5816                      vla_ptr_t *state_stack)

5817 {

5818   state_t state;

5819   alt_state_t alt_state, curr_alt_state;

5820   alt_state_t new_alt_state;

5821   arc_t curr_arc;

5822   arc_t next_arc;

5823   state_t state_in_table;

5824   state_t temp_state;

5825   alt_state_t canonical_alt_states_list;

5826   int alts_number;

5827   int new_state_p = 0;

5828

5829   if (arcs_marked_by_insn == NULL)

5830     return new_state_p;

5831   if (arcs_marked_by_insn->next_arc_marked_by_insn == NULL)

5832     state = arcs_marked_by_insn->to_state;

5833   else

5834   {

5835     if (!ndfa_flag )

5836       abort ();

5837     /* Create composed state.  */

5838     state = get_free_state (0, arcs_marked_by_insn->to_state->automaton);

5839     curr_alt_state = NULL;

5840     for (curr_arc = arcs_marked_by_insn;

5841         curr_arc != NULL;

5842         curr_arc = curr_arc->next_arc_marked_by_insn)

5843       if (curr_arc->to_state->component_states == NULL)

5844       {

5845         new_alt_state = get_free_alt_state ();

5846         new_alt_state->next_alt_state = curr_alt_state;

5847         new_alt_state->state = curr_arc->to_state;

5848         curr_alt_state = new_alt_state;

5849       }

5850       else

5851         for (alt_state = curr_arc->to_state->component_states;

5852             alt_state != NULL;

5853             alt_state = alt_state->next_sorted_alt_state)

5854         {

5855           new_alt_state = get_free_alt_state ();

5856           new_alt_state->next_alt_state = curr_alt_state;

5857           new_alt_state->state = alt_state->state;

5858           if (alt_state->state->component_states != NULL)

5859             abort ();

5860           curr_alt_state = new_alt_state;

5861         }

5862       /* There are not identical sets in the alt state list.  */

5863       canonical_alt_states_list = uniq_sort_alt_states (curr_alt_state);

5864       if (canonical_alt_states_list->next_sorted_alt_state == NULL)

5865       {

5866         temp_state = state;

5867         state = canonical_alt_states_list->state;

5868         free_state (temp_state);

5869       }

5870       else

5871       {

5872         state->component_states = canonical_alt_states_list;

5873         state_in_table = insert_state (state);

5874         if (state_in_table != state)

5875         {

5876           if (!state_in_table->it_was_placed_in_stack_for_DFA_forming)

5877             abort ();

5878           free_state (state);

5879            state = state_in_table;

5880         }

5881         else

5882         {

5883           if (state->it_was_placed_in_stack_for_DFA_forming)

5884             abort ();

5885           new_state_p = 1;

5886           for (curr_alt_state = state->component_states;

5887               curr_alt_state != NULL;

5888               curr_alt_state = curr_alt_state->next_sorted_alt_state)

5889              for (curr_arc = first_out_arc (curr_alt_state->state);

5890                  curr_arc != NULL;

5891                   curr_arc = next_out_arc (curr_arc))

5892                add_arc (state, curr_arc->to_state, curr_arc->insn, 1);

5893         }

5894         arcs_marked_by_insn->to_state = state;

5895         for (alts_number = 0,

5896             curr_arc = arcs_marked_by_insn->next_arc_marked_by_insn;

5897             curr_arc != NULL;

5898             curr_arc = next_arc)

5899         {

5900           next_arc = curr_arc->next_arc_marked_by_insn;

5901           remove_arc (original_state, curr_arc);

5902           alts_number++;

5903         }

5904         arcs_marked_by_insn->state_alts = alts_number;

5905       }

5906   }

5907   if (!state->it_was_placed_in_stack_for_DFA_forming)

5908   {

5909     state->it_was_placed_in_stack_for_DFA_forming = 1;

5910     VLA_PTR_ADD (*state_stack, state);

5911   }

5912   return new_state_p;

5913 }

 

curr_alt_state in our example is a list like: curr_alt_state(SA)->next_alt_state(SB)-> next_alt_state(SC). Then the list is passed to uniq_sort_alt_states which sorts alt_states_list and removes duplicated alt states from the list. Here, for our nondeterministic example, the list is unchanged.

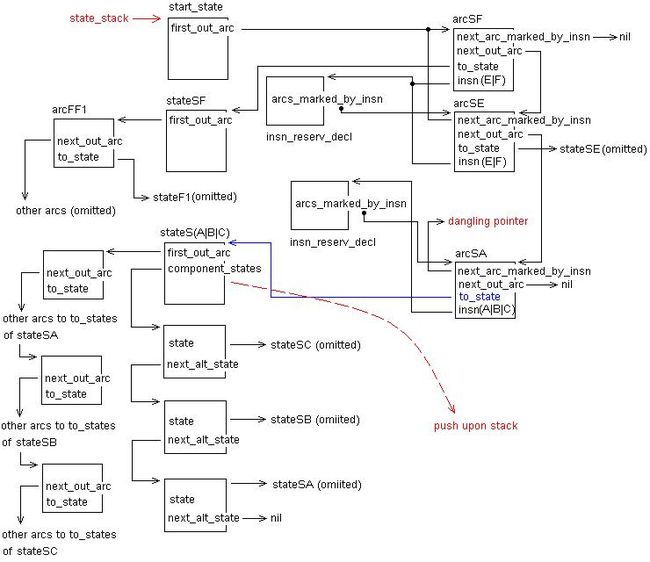
At line 5864, if next_sorted_alt_state is not NULL, then state at line 5872 is newly created; it must not be present in the state_table . Then we enter line 5882, and the data created in create_composed_state is shown in below figure.

figure 79  : building DFA, stage 3

As we mentioned before, once new state is created, all transition destinations of all alternatives of current state are set as transition destinations for this new state. Then current state can transit to this new state deterministically in theoretical, notice that in figure arcSA is left with field in blue revised and other arcs for those alternatives from current state are removed. Following, this new state will be put into state_stack . And repeat the above steps upon this state. NDFA_to_DFA will not exit until there is no state in state_stack (that is, no state having nondeterministic transition).