立方体画家消隐算法与Z-Buffer消隐算法 比较

立方体画家消隐算法与Z-Buffer消隐算法在别的方面有所类似,在<计算机图形学实践教程VC++ 孔令德>中,两个算法用到的立方体都是正交投影,而不是透视投影,即立方体远离视点时显示的立方体仍然是原大小,不变化.只是二种算法核心思想不同:

 

一. 立方体Z-Buffer消隐是对于某一个像素点,不必对在靠近或远离视点的面进行排序,只需在遍历各面后找出该像素的深度最大的点(Z最大,即离视点最近)(先找深度大的点setPixel(),如果以后还有深度更大的,则通过设置新的颜色setPixel()来覆盖以前的点,其中要注意以yi为扫描线时,扫描线可能不与屏幕平行,可能是倾斜着的,就像把opengl的X轴绕Y轴旋转一个角度,如向量(1,-1,0),此次每次随x增大,z也会相应变化-A/C,其中(A,B,C)为该面的法向量),可以说它是对逐个像素进行深度判断进行的.主要代码如下:

for(T1=HeadE;T1!=NULL;T1=T1->next)//填充扫描线和多边形相交的区间

              {

                     if(In==false)

                     {

                            xb=T1->x;

                            CurDeep=-(xb*A+CurrentB->ScanLine*B+D)/C;//z=-(Ax+By+D)/C

                            In=true;//每访问一个结点,把In值取反一次

                     }

                     else//如果In值为真，则填充从当前结点的x值开始到下一结点的x值结束的区间

                     {

                            xe=T1->x;

                            for(double x=xb;x<=xe;x++)

                            {                                

                                   if(CurDeep>=ZB[ROUND(x)+200][CurrentB->ScanLine+200])//如果新的采样点的深度大于原采样点的深度,因为绘制每个面都会调用该函数,故以后的面中如果有更深度更大的点,则会覆盖以前的点的颜色.注意,此处要遍历[xb,xe]上的每个整数点,绘制连续的像素点,以连成一条线                             .

{

                                          ZB[ROUND(x)+200][CurrentB->ScanLine+200]=CurDeep;//xy坐标与数组下标保持一致，加200

                                          mdc->SetPixel(ROUND(x),CurrentB->ScanLine,RGB[Face]);

                                   }

                                   CurDeep+=DeepStep;                               

                            }

                            In=false;

                     }           

              }    

 

 

 

二.立方体画家消隐算法是对每个面求Z最小的值MinDeep,然后对这6个面按MinDeep值从小到大进行排序(即离视点近的面后画,来覆盖离视点远的面),然后再按从远到近画六个面即可.不过这种算法还是有局限的,它只是针对包围体(如立方体)来说的,如果对于那种不闭合的体(如2个相交且无限延伸的平面(就像opengl坐标系上的平面XOY和平面YOZ)),则会出现问题. 主要代码如下:

for(T1=HeadE;T1!=NULL;T1=T1->next)

       {         

              xb=T1->x;            CurDeep=-(xb*A+CurrentB->ScanLine*B+D)/C;//z=-(Ax+By-D)/C                               

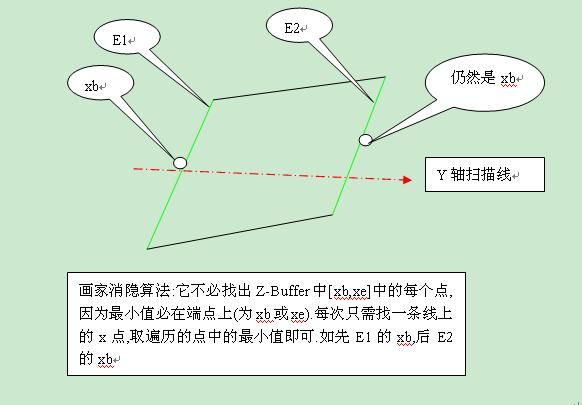
              if(CurDeep<=F[Face].MinDeep)// 找一个面上深度最小(即Z最小,最远离视点)的点,此处不像Z-Buffer那样每次找2个点xb,xe,且需要遍历其中的每个x点,它只需找到最小值,而这个最小值必定在线段的2个端点上(要么是xb,要么是xe),故可以一个端点一个端点地访问找出Z的最小值即可,而且它暂时不绘制像素点,而是在最后把6个面按先远后近的顺序进行排序后再绘制这6个面.

              {

                  F[Face].MinDeep=CurDeep;//同上一行记录

              }

              CurDeep+=DeepStep;

}