三维凸包
三维凸包
3D Convex Hull
Problem Description
There are N points in 3D-space which make up a 3D-Convex hull*. How many faces does the 3D-convexhull have? It is guaranteed that all the points are not in the same plane.
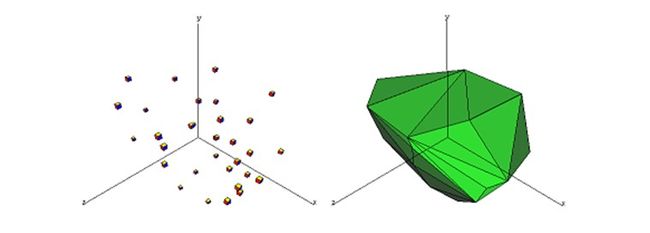
In case you don’t know the definition of convex hull, here we give you a clarification from Wikipedia:
*Convex hull: In mathematics, the convex hull, for a set of points X in a real vector space V, is the minimal convex set containing X.
Input
There are several test cases. In each case the first line contains an integer N indicates the number of 3D-points (3< N <= 300), and then N lines follow, each line contains three numbers x, y, z (between -10000 and 10000) indicate the 3d-position of a point.
Output
Output the number of faces of the 3D-Convex hull.
Sample Input
7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 -0.1 7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 0.1
Sample Output
8 5
Source
2010 Asia Regional Harbin
分析:给出三维空间中的n个顶点,求解由这n个顶点构成的凸包表面的多边形个数.
增量法求解:首先任选4个点形成的一个四面体,然后每次新加一个点,分两种情况:
1> 在凸包内,则可以跳过
2> 在凸包外,找到从这个点可以"看见"的面S(看不看得见可以用法向量,看点是否在面外侧),删除这些面S,然后对于S的每条边E进行判断,看该点还能否看到这些边E的另一侧的面,这样深度搜索判断。
下面是三维凸包的AC代码:(15MS 488KB)
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
#define PR 1e-8
#define N 310
struct TPoint
{
double x,y,z;
TPoint(){}
TPoint(double _x,double _y,double _z):x(_x),y(_y),z(_z){}
TPoint operator-(const TPoint p) {return TPoint(x-p.x,y-p.y,z-p.z);}
TPoint operator*(const TPoint p) {return TPoint(y*p.z-z*p.y,z*p.x-x*p.z,x*p.y-y*p.x);}//叉积
double operator^(const TPoint p) {return x*p.x+y*p.y+z*p.z;}//点积
};
struct fac//
{
int a,b,c;//凸包一个面上的三个点的编号
bool ok;//该面是否是最终凸包中的面
};
struct T3dhull
{
int n;//初始点数
TPoint ply[N];//初始点
int trianglecnt;//凸包上三角形数
fac tri[N];//凸包三角形
int vis[N][N];//点i到点j是属于哪个面
double dist(TPoint a){return sqrt(a.x*a.x+a.y*a.y+a.z*a.z);}//两点长度
double area(TPoint a,TPoint b,TPoint c){return dist((b-a)*(c-a));}//三角形面积*2
double volume(TPoint a,TPoint b,TPoint c,TPoint d){return (b-a)*(c-a)^(d-a);}//四面体有向体积*6
double ptoplane(TPoint &p,fac &f)//正:点在面同向
{
TPoint m=ply[f.b]-ply[f.a],n=ply[f.c]-ply[f.a],t=p-ply[f.a];
return (m*n)^t;
}
void deal(int p,int a,int b)
{
int f=vis[a][b];//与当前面(cnt)共边(ab)的那个面
fac add;
if(tri[f].ok)
{
if((ptoplane(ply[p],tri[f]))>PR) dfs(p,f);//如果p点能看到该面f,则继续深度探索f的3条边,以便更新新的凸包面
else//否则因为p点只看到cnt面,看不到f面,则p点和a、b点组成一个三角形。
{
add.a=b,add.b=a,add.c=p,add.ok=1;
vis[p][b]=vis[a][p]=vis[b][a]=trianglecnt;
tri[trianglecnt++]=add;
}
}
}
void dfs(int p,int cnt)//维护凸包,如果点p在凸包外更新凸包
{
tri[cnt].ok=0;//当前面需要删除,因为它在更大的凸包里面
//下面把边反过来(先b,后a),以便在deal()中判断与当前面(cnt)共边(ab)的那个面。即判断与当头面(cnt)相邻的3个面(它们与当前面的共边是反向的,如下图中(1)的法线朝外(即逆时针)的面130和312,它们共边13,但一个方向是13,另一个方向是31)
deal(p,tri[cnt].b,tri[cnt].a);
deal(p,tri[cnt].c,tri[cnt].b);
deal(p,tri[cnt].a,tri[cnt].c);
}
bool same(int s,int e)//判断两个面是否为同一面
{
TPoint a=ply[tri[s].a],b=ply[tri[s].b],c=ply[tri[s].c];
return fabs(volume(a,b,c,ply[tri[e].a]))<PR
&&fabs(volume(a,b,c,ply[tri[e].b]))<PR
&&fabs(volume(a,b,c,ply[tri[e].c]))<PR;
}
void construct()//构建凸包
{
int i,j;
trianglecnt=0;
if(n<4) return ;
bool tmp=true;
for(i=1;i<n;i++)//前两点不共点
{
if((dist(ply[0]-ply[i]))>PR)
{
swap(ply[1],ply[i]); tmp=false; break;
}
}
if(tmp) return;
tmp=true;
for(i=2;i<n;i++)//前三点不共线
{
if((dist((ply[0]-ply[1])*(ply[1]-ply[i])))>PR)
{
swap(ply[2],ply[i]); tmp=false; break;
}
}
if(tmp) return ;
tmp=true;
for(i=3;i<n;i++)//前四点不共面
{
if(fabs((ply[0]-ply[1])*(ply[1]-ply[2])^(ply[0]-ply[i]))>PR)
{
swap(ply[3],ply[i]); tmp=false; break;
}
}
if(tmp) return ;
fac add;
for(i=0;i<4;i++)//构建初始四面体(4个点为ply[0],ply[1],ply[2],ply[3])
{
add.a=(i+1)%4,add.b=(i+2)%4,add.c=(i+3)%4,add.ok=1;
if((ptoplane(ply[i],add))>0) swap(add.b,add.c);//保证逆时针,即法向量朝外,这样新点才可看到。
vis[add.a][add.b]=vis[add.b][add.c]=vis[add.c][add.a]=trianglecnt;//逆向的有向边保存
tri[trianglecnt++]=add;
}
for(i=4;i<n;i++)//构建更新凸包
{
for(j=0;j<trianglecnt;j++)//对每个点判断是否在当前3维凸包内或外(i表示当前点,j表示当前面)
{
if(tri[j].ok&&(ptoplane(ply[i],tri[j]))>PR)//对当前凸包面进行判断,看是否点能否看到这个面
{
dfs(i,j); break;//点能看到当前面,更新凸包的面(递归,可能不止更新一个面)。当前点更新完成后break跳出循环
}
}
}
int cnt=trianglecnt;//这些面中有一些tri[i].ok=0,它们属于开始建立但后来因为在更大凸包内故需删除的,所以下面几行代码的作用是只保存最外层的凸包
trianglecnt=0;
for(i=0;i<cnt;i++)
{
if(tri[i].ok)
tri[trianglecnt++]=tri[i];
}
}
double area()//表面积
{
double ret=0;
for(int i=0;i<trianglecnt;i++)
ret+=area(ply[tri[i].a],ply[tri[i].b],ply[tri[i].c]);
return ret/2;
}
double volume()//体积
{
TPoint p(0,0,0);
double ret=0;
for(int i=0;i<trianglecnt;i++)
ret+=volume(p,ply[tri[i].a],ply[tri[i].b],ply[tri[i].c]);
return fabs(ret/6);
}
int facetri() {return trianglecnt;}//表面三角形数
int facepolygon()//表面多边形数
{
int ans=0,i,j,k;
for(i=0;i<trianglecnt;i++)
{
for(j=0,k=1;j<i;j++)
{
if(same(i,j)) {k=0;break;}
}
ans+=k;
}
return ans;
}
}hull;
int main()
{
while(~scanf("%d",&hull.n))
{
int i;
for(i=0;i<hull.n;i++)
scanf("%lf%lf%lf",&hull.ply[i].x,&hull.ply[i].y,&hull.ply[i].z);
hull.construct();
printf("%d\n",hull.facepolygon());
}
return 0;
}
设初始4点组成的四面体为0123,当加入p点时,举3个例子:
(1)设对边13,p只能看到面123,不能看到面130:则只需去掉以前的面123并添加3个面(1p3,1p2,2p3)。函数中调用了dfs->deal。如下图:
参考文档:
http://www.cnblogs.com/Mu-Tou/archive/2011/08/12/2136748.html
http://blog.sina.com.cn/s/blog_732dd9320100sizg.html
http://blog.sina.com.cn/s/blog_732dd9320100sizm.html