CUDA编程(八)树状加法
CUDA编程(八)
树状加法
上一篇博客我们介绍了ShareMemory和Thread同步,最后利用这些知识完成了block内部线程结果的加和,减轻了CPU的负担,结果还是比较令人满意的,但是block的加和工作是使用一个thread0单线程完成的,这点还是有待改进的。
那么这个单线程的加法部分如何解决呢?我们知道GPU上的程序只有并行才能发挥其优势,所以我们自然想到这个加法能不能并行呢?答案当然是可行的,我们可以利用树状加法的方式将加法并行,这也体现了我们之前提到的,一个优秀的CUDA程序是需要一个优秀的算法为基础的。
树状加法
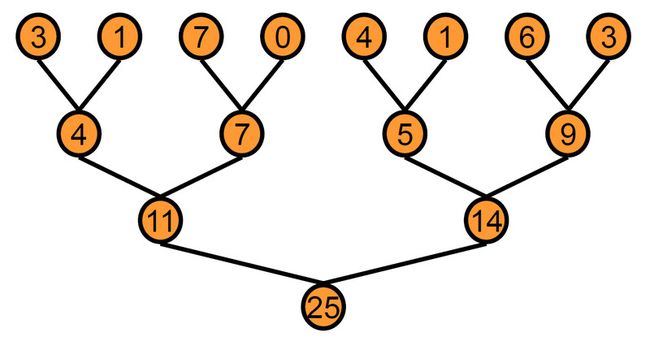
我们传统的加法 a + b + c + d ,只能在一个线程上进行,但是我们也很容易想到,如果把加法分成多步执行,比如先算 a+b,c+d,再把他们的结果相加,通过这样的方式我们就可以把任务分开,也就是可以并行了,这就是树状加法:
通过这种方式我们就可以把256个数的加法进行并行了。
树状加法的实现
上图是树状加法的一个示意图,示意图中第一排每一个格子就是一个线程的结果,保存在shared[],暂且把shared[0]简写为 sh0,我们可以清楚的看到计算的过程:
sh0=sh0+sh1, sh2=sh2+sh3, sh4=sh4+sh5...
同步
sh0=sh0+sh2;sh4=sh4+sh6...
同步
...
最后结果在sh0里其实树状加法可以写成一个很简单的while循环:
int offset = 1, mask = 1;
while(offset < THREAD_NUM)
{
if((tid & mask) == 0)
{
shared[tid] += shared[tid + offset];
}
offset += offset;
mask = offset + mask;
__syncthreads();
}下面我们就来看看这个while循环:
注意& 按位“与”,只有1&1 = 1
tid=0时,mask = 1,0&1=0,所以shared[0] = sh0 + sh1,完成第一步的前两个相加。
tid=1时,mask = 1,1&1=1,不作运算。
tid=2时,mask = 1,10&01 = 00,所以shared[2] = sh2 + sh3
tid=3时,mask = 1,11&01 = 01,不作运算。
…
可以看出来这是第一层的计算
同步之后第二层:
offset=1+1=2,mask=2+1=3;
tid=0时,mask = 3,0&11=0,所以shared[0] = sh0 + sh2,完成第二步的前两个相加。
tid=1时,mask = 3,1&11=1,不作运算。
tid=2时,mask = 3,10&11 = 10,不作运算。
tid=3时,mask = 3,11&11 = 01,不作运算。
tid=4时,mask = 3,100&011 = 000,所以shared[4] = sh4 + sh6
后面都以此类推,直到offset 大于等于线程数就跳出了
最终的结果就在shared[0]内,所以下一步用线程0把结果保存就OK了:
if(tid == 0) { result[bid] = shared[0]; }所以比起上一版的程序,我们只用改动核函数里面的加和部分就OK了,下面是改好的核函数:
核函数:
// __global__ 函数 (GPU上执行) 计算立方和
__global__ static void sumOfSquares(int *num, int* result, clock_t* time)
{
//声明一块共享内存
extern __shared__ int shared[];
//表示目前的 thread 是第几个 thread(由 0 开始计算)
const int tid = threadIdx.x;
//表示目前的 thread 属于第几个 block(由 0 开始计算)
const int bid = blockIdx.x;
shared[tid] = 0;
int i;
//记录运算开始的时间
clock_t start;
//只在 thread 0(即 threadIdx.x = 0 的时候)进行记录,每个 block 都会记录开始时间及结束时间
if (tid == 0) time[bid] = clock();
//thread需要同时通过tid和bid来确定,同时不要忘记保证内存连续性
for (i = bid * THREAD_NUM + tid; i < DATA_SIZE; i += BLOCK_NUM * THREAD_NUM) {
shared[tid] += num[i] * num[i] * num[i];
}
//同步 保证每个 thread 都已经把结果写到 shared[tid] 里面
__syncthreads();
//树状加法
int offset = 1, mask = 1;
while (offset < THREAD_NUM)
{
if ((tid & mask) == 0)
{
shared[tid] += shared[tid + offset];
}
offset += offset;
mask = offset + mask;
__syncthreads();
}
//计算时间,记录结果,只在 thread 0(即 threadIdx.x = 0 的时候)进行,每个 block 都会记录开始时间及结束时间
if (tid == 0)
{
result[bid] = shared[0];
time[bid + BLOCK_NUM] = clock();
}
}运行结果:
我们看到比起上一次没用树状加法的144185个周期,这次只用了133738个周期,总的来说这个结果还是非常不错的,甚至和完全不在GPU上加和的程序速度差不多,这是因为,在完全不在 GPU 上进行加总的版本,写入到 global memory 的数据数量很大(8192 个数字),这对效率也会有影响。所以,这一版程序不但在 CPU 上的运算需求降低,在 GPU 上也能跑的更快~
总结:
这篇博客我们主要介绍了怎么去把加法进行并行,利用树状加法,最终并行了之前效率比较差的加和部分,到这里为止,这个程序的一般性优化也做完了,因为程序也很简单,所以很多的方面都无法体现,比如之前提过的GPU运算的一大问题在于精度,还有尽可能减少访存这些方面的优化都没有体现出来,所以下一篇博客我们准备真正向应用CUDA靠拢,去进行矩阵计算~
希望我的博客能帮助到大家~
参考资料:《深入浅出谈CUDA》